График Джонсона

График Джонсона
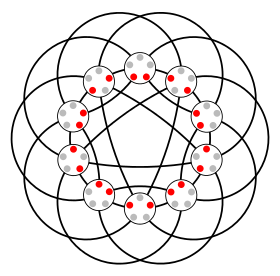Граф Джонсона J (5,2)
Назван в честь	Селмер М. Джонсон
Вершины	${\binom {n}{k}}$
Края	${\frac {1}{2}}k(n-k){\binom {n}{k}}$
Диаметр	$\min(k,n-k)$
Характеристики	$k(n-k)$-обычный Вершинно-транзитивный Дистанционно-транзитивный Связанный с Гамильтоном
Обозначения	$J(n,k)$
Таблица графиков и параметров

Графы Джонсона — это особый класс неориентированных графов, определяемых на основе систем множеств. Вершины графа Джонсона $J(n,k)$ являются $k$-элементные подмножества $n$- набор элементов; две вершины являются смежными, если пересечение двух вершин (подмножеств) содержит $(k-1)$-элементы. Оба графа Джонсона и тесно связанная с ним схема Джонсона названы в честь Сельмера М. Джонсона .

Особые случаи

• Оба $J(n,1)$ и $J(n,n-1)$ являются полным графом K _n .
• $J(4,2)$ – октаэдрический граф .
• $J(5,2)$ является дополнением графа Петерсена , отсюда график линейный K ₅ . В более общем плане для всех $n$, график Джонсона $J(n,2)$ является линейным графом K _n и дополнением графа Кнезера $K(n,2).$

Теоретико-графовые свойства

• $J(n,k)$ изоморфен $J(n,n-k).$
• Для всех $0\leq j\leq \operatorname {diam} (J(n,k))$, любая пара вершин на расстоянии $j$ делиться $k-j$ элементы общие.
• $J(n,k)$ является гамильтоновым связным , то есть каждая пара вершин образует концы гамильтонова пути в графе. В частности, это означает, что он имеет гамильтонов цикл.
• Также известно, что граф Джонсона $J(n,k)~$ является $~k(n-k)$-вершинно-связный.
• $J(n,k)$ образует граф вершин и ребер ( n − 1)-мерного многогранника , называемый гиперсимплексом .
• число клик ​ $J(n,k)$ задается выражением через наименьшее и наибольшее собственные значения: $\omega (J(n,k))=1-{\tfrac {\lambda _{\max }}{\lambda _{\min }}}.$
• Хроматическое число ​ $J(n,k)$ самое большее $n,\chi (J(n,k))\leq n.$
• Каждый граф Джонсона является локально сеточным что означает, что индуцированный подграф соседей , любой вершины является ладейным графом . Точнее, в графе Джонсона $J(n,k)$, каждое соседство представляет собой $k\times (n-k)$ ладейный граф.

Группа автоморфизмов

Существует дистанционно-транзитивная подгруппа $\operatorname {Aut} (J(n,k))$ изоморфен $\operatorname {Sym} (n)$. Фактически, $\operatorname {Aut} (J(n,k))\cong \operatorname {Sym} (n)$, за исключением того случая, когда $n=2k\geq 4$, $\operatorname {Aut} (J(n,k))\cong \operatorname {Sym} (n)\times C_{2}$.

Массив пересечений

Вследствие транзитивности расстояния, $J(n,k)$ также является дистанционно регулярным . Сдача в аренду $d$ обозначим его диаметр, массив пересечений $J(n,k)$ дается

$\left\{b_{0},\ldots ,b_{d-1},c_{1},\ldots c_{d}\right\}$

где:

${\begin{aligned}b_{j}&=(k-j)(n-k-j)&&0\leq j<d\\c_{j}&=j^{2}&&0<j\leq d\end{aligned}}$

Оказывается, если только $J(n,k)$ является $J(8,2)$, его массив пересечений не используется совместно с каким-либо другим отдельным дистанционно-регулярным графом; массив пересечений $J(8,2)$ используется совместно с тремя другими дистанционно регулярными графами, которые не являются графами Джонсона.

Собственные значения и собственные векторы

• Характеристический полином $J(n,k)$ дается

$\phi (x):=\prod _{j=0}^{\operatorname {diam} (J(n,k))}\left(x-A_{n,k}(j)\right)^{{\binom {n}{j}}-{\binom {n}{j-1}}}.$

где $A_{n,k}(j)=(k-j)(n-k-j)-j.$

• Собственные векторы $J(n,k)$ иметь явное описание.

Схема Джонсона

График Джонсона $J(n,k)$ тесно связана со схемой Джонсона — схемой ассоциации , в которой каждой паре наборов k -элементов соответствует число, вдвое меньшее симметричной разности двух наборов. Граф Джонсона имеет ребро для каждой пары множеств на расстоянии один в схеме ассоциации, а расстояния в схеме ассоциации - это в точности расстояния кратчайшего пути в графе Джонсона.

Схема Джонсона также связана с другим семейством дистанционно-транзитивных графов, нечетными графами , вершины которых $k$-элементные подмножества $(2k+1)$-элементное множество, ребра которого соответствуют непересекающимся парам подмножеств.

Открытые проблемы

Свойства расширения вершин графов Джонсона, а также структура соответствующих экстремальных множеств вершин заданного размера до конца не изучены. Однако недавно была получена асимптотически точная нижняя граница расширения больших наборов вершин.

В общем, определение хроматического числа графа Джонсона является открытой проблемой.

См. также

• Грассман граф

Внешние ссылки

• Вайсштейн, Эрик В. , «График Джонсона» , MathWorld
• Брауэр, Андрис Э. , Графики Джонсона