Гиперсимплекс
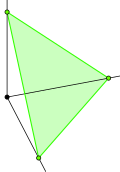 | 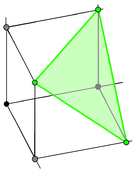 |
Гиперплоскость: | Гиперплоскость: |
|---|
В полиэдральной гиперсимплекс комбинаторике — выпуклый многогранник , обобщающий симплекс . Оно определяется двумя целыми числами и , и определяется как выпуклая оболочка -мерные векторы , коэффициенты которых состоят из те и нули. Эквивалентно, можно получить, разрезав -мерный единичный гиперкуб с гиперплоскостью уравнения и по этой причине это -мерный многогранник, когда . [1]
Характеристики
[ редактировать ]Количество вершин является . [1] Граф, образованный вершинами и ребрами гиперсимплекса это график Джонсона . [2]
Альтернативные конструкции
[ редактировать ]Альтернативная конструкция (для ) — взять выпуклую оболочку всех -мерный -векторы, которые имеют либо или ненулевые координаты. Преимущество этого метода заключается в том, что он работает в пространстве той же размерности, что и полученный многогранник, но недостатком является то, что создаваемый им многогранник менее симметричен (хотя комбинаторно эквивалентен результату другой конструкции).
Гиперсимплекс также является многогранником матроида для однородного матроида с элементы и ранг . [3]
Примеры
[ редактировать ]Гиперсимплекс это -симплекс (и, следовательно, он имеет вершины).Гиперсимплекс представляет собой октаэдр , а гиперсимплекс представляет собой выпрямленный 5-клеточный .
Как правило, гиперсимплекс, , соответствует однородному многограннику , являющемуся - исправлено -мерный симплекс с вершинами, расположенными в центре всех -мерные грани -мерный симплекс.
| Имя | Равносторонний треугольник | Тетраэдр (3-симплекс) | Октаэдр | 5-клеточный (4-симплекс) | Исправленный 5-клеточный | 5-симплекс | Исправленный 5-симплекс | биректифицированный 5-симплекс |
|---|---|---|---|---|---|---|---|---|
| Δd k , k знак равно d , ) ( знак равно ( d , d - k ) | (3,1) (3,2) | (4,1) (4,3) | (4,2) | (5,1) (5,4) | (5,2) (5,3) | (6,1) (6,5) | (6,2) (6,4) | (6,3) |
| Вершины | 3 | 4 | 6 | 5 | 10 | 6 | 15 | 20 |
| г - координаты | (0,0,1) (0,1,1) | (0,0,0,1) (0,1,1,1) | (0,0,1,1) | (0,0,0,0,1) (0,1,1,1,1) | (0,0,0,1,1) (0,0,1,1,1) | (0,0,0,0,0,1) (0,1,1,1,1,1) | (0,0,0,0,1,1) (0,0,1,1,1,1) | (0,0,0,1,1,1) |
| Изображение |  |  |  |  |  | |||
| Графики |  Дж (3.1) = К 2 |  Дж (4,1) = К 3 |  Дж (4,2) = Т(6,3) |  Дж (5,1) = К 4 |  Дж (5,2) |  Дж (6.1) = К 5 |  Дж (6,2) |  Дж (6,3) |
| Коксетер диаграммы | ||||||||
| Шлефли символы | {3} = р {3} | {3,3} = 2 р {3,3} | г{3,3} = {3,4} | {3,3,3} = 3р { 3,3,3} | р {3,3,3} = 2 р {3,3,3} | {3,3,3,3} = 4р { 3,3,3,3} | р {3,3,3,3} = 3р { 3,3,3,3} | 2р { 3,3,3,3 } |
| Фасеты | { } | {3} | {3,3} | {3,3}, {3,4} | {3,3,3} | {3,3,3}, г {3,3,3} | р {3,3,3} | |
История
[ редактировать ]Гиперсимплексы были впервые изучены и названы при вычислении характеристических классов (важная тема в алгебраической топологии ) Габриеловым, Гельфандом и Лосиком (1975) . [4] [5]
Ссылки
[ редактировать ]- ^ Jump up to: Перейти обратно: а б Миллер, Эзра; Райнер, Виктор; Штурмфельс, Бернд , Геометрическая комбинаторика , Математическая серия IAS / Парк-Сити, том. 13, Американское математическое общество, с. 655, ISBN 9780821886953 .
- ^ Рисполи, Фред Дж. (2008), Граф гиперсимплекса , arXiv : 0811.2981 , Bibcode : 2008arXiv0811.2981R .
- ^ Гретшель, Мартин (2004), «Системы однородных множеств по мощности, циклы в матроидах и связанные с ними многогранники», The Sharpest Cut: The Impact of Manfred Padberg and His Work , MPS/SIAM Ser. Optim., SIAM, Филадельфия, Пенсильвания, стр. 99–120, MR 2077557 . См., в частности, замечания после предложения 8.20 на с. 114 .
- ^ Габриэлов А.М.; Гельфанд, И.М .; Лосик М. В. (1975), "Комбинаторное вычисление характеристических классов. I, II", Академия наук СССР , 9 (2): 12–28, там же. 9 (1975), вып. 3, 5–26, МР 0410758 .
- ^ Циглер, Гюнтер М. (1995), Лекции по многогранникам , Тексты для аспирантов по математике, том. 152, Спрингер-Верлаг, Нью-Йорк, с. 20, номер домена : 10.1007/978-1-4613-8431-1 , ISBN. 0-387-94365-Х , МР 1311028 .
Дальнейшее чтение
[ редактировать ]- Хиби, Такаюки; Солус, Лиам (2016), «Аспекты r -стабильного (n , k) -гиперсимплекса», Annals of Combinatorics , 20 : 815–829, arXiv : 1408.5932 , Bibcode : 2014arXiv1408.5932H , doi : 10.1007/s00026-016 -0325-х .









![{\displaystyle [0,1]^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e13ae4917276744b214714a20b3cb8ee305e309d)











