Катушка Гельмгольца

Катушка Гельмгольца — устройство для создания области почти однородного магнитного поля , названное в честь немецкого физика Германа фон Гельмгольца . Он состоит из двух электромагнитов , расположенных на одной оси, по которым протекает одинаковый электрический ток в одном направлении. Помимо создания магнитных полей, катушки Гельмгольца также используются в научной аппаратуре для подавления внешних магнитных полей, таких как магнитное поле Земли.

Когда пара двух электромагнетиков катушки Гельмгольца несет равный электрический ток в противоположном направлении, это известно как катушка антиГельмгольца , которая создает область почти однородного градиента магнитного поля и используется для создания магнитных ловушек в атомной физике. эксперименты.

Описание

Пара Гельмгольца состоит из двух одинаковых круговых магнитных катушек, расположенных симметрично вдоль общей оси, по одной с каждой стороны экспериментальной площадки и разделенных расстоянием $h$ равен радиусу $R$ катушки. Каждая катушка несет одинаковый электрический ток в одном направлении. ^[1]

Параметр $h=R$ , что и определяет пару Гельмгольца, минимизирует неоднородность поля в центре катушек, в смысле установки $\partial ^{2}B/\partial x^{2}=0$ ^[2] (это означает, что первая ненулевая производная равна $\partial ^{4}B/\partial x^{4}$ как объяснено ниже), но оставляет разницу в напряженности поля между центром и плоскостями катушек примерно 7%.Несколько большее значение $h$ уменьшает разность полей между центром и плоскостями катушек за счет ухудшения однородности поля в области вблизи центра, измеряемой по формуле $\partial ^{2}B/\partial x^{2}$ . ^[3]

Когда пара катушек Гельмгольца пропускает равный электрический ток в противоположном направлении, они создают область почти однородного градиента магнитного поля. Это известно как катушка анти-Гельмгольца и используется для создания магнитных ловушек в экспериментах по атомной физике.

В некоторых приложениях катушка Гельмгольца используется для нейтрализации магнитного поля Земли , создавая область с напряженностью магнитного поля, намного ближе к нулю. ^[4]

Математика

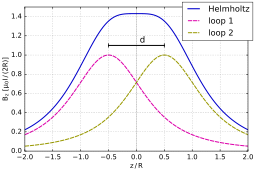
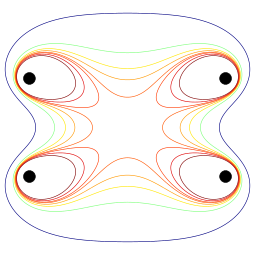
Расчет точного магнитного поля в любой точке пространства математически сложен и предполагает изучение функций Бесселя . Вдоль оси пары катушек дело обстоит проще, и удобно думать о разложении напряженности поля в ряд Тейлора как функции $x$ , расстояние от центральной точки пары катушек вдоль оси.По симметрии члены нечетного порядка в разложении равны нулю. Расположив витки так, чтобы начало координат $x=0$ является точкой перегиба напряженности поля, создаваемой каждой катушкой в отдельности, можно гарантировать, что порядок $x^{2}$ член также равен нулю, и, следовательно, главный непостоянный член имеет порядок $x^{4}$ . Точка перегиба простой катушки расположена вдоль оси катушки на расстоянии $R/2$ от его центра. Таким образом, места для двух катушек $x=\pm R/2$ .

Подробный расчет ниже дает точное значение магнитного поля в центральной точке. Если радиус равен R , количество витков в каждой катушке n и ток через катушки I , то магнитное поле B в средней точке между катушками будет определяться выражением

B={\left({\frac {4}{5}}\right)}^{3/2}{\frac {\mu _{0}nI}{R}},

где $\mu _{0}$ – проницаемость свободного пространства ( $4\pi \times 10^{-7}{\text{ T}}\cdot {\text{m/A}}$ ) .

Вывод

Начнем с формулы для осевого поля, создаваемого одной проволочной петлей, которая сама выведена из закона Био-Савара : ^[5]

B_{1}(x)={\frac {\mu _{0}IR^{2}}{2(R^{2}+x^{2})^{3/2}}}=\xi (x){\frac {\mu _{0}I}{2R}}.

Здесь

\mu _{0}\;

= константа проницаемости =

4\pi \times 10^{-7}{\text{ T}}\cdot {\text{m/A}}=1.257\times 10^{-6}{\text{ T}}\cdot {\text{m/A}},

I\;

= ток катушки, в амперах ,

R\;

= радиус катушки, в метрах,

x\;

= расстояние катушки по оси до точки в метрах,

\xi (x)=[1+(x/R)^{2}]^{-3/2}\;

- безразмерный коэффициент, зависящий от расстояния.

Катушка Гельмгольца состоит из n витков провода, поэтому эквивалентный ток в одновитковой катушке в n раз превышает ток I в n -витковой катушке. Замена nI на I в приведенной выше формуле дает поле для n -витковой катушки:

B_{1}(x)=\xi (x){\frac {\mu _{0}nI}{2R}}.

Для $x\ll R$ , коэффициент расстояния $\xi (x)=[1+(x/R)^{2})]^{-3/2}\;$ можно разложить в ряд Тейлора как:

$\xi (x)=1-{\frac {3}{2}}(x/R)^{2}+{\mathcal {O}}((x/R)^{4}).$

В паре Гельмгольца две катушки расположены на $x=\pm R/2$ , поэтому напряженность B-поля при любом $x$ будет:

{\begin{aligned}B(x)&={\frac {\mu _{0}nI}{2R}}\left[\xi (x-R/2)+\xi (x+R/2)\right]\\&={\frac {\mu _{0}nI}{2R}}\left([1+(x/R-1/2)^{2}]^{-3/2}+[1+(x/R+1/2)^{2}]^{-3/2}\right)\\\end{aligned}}

Точки рядом с центром (на полпути между двумя катушками) имеют $x\ll R$ и Тейлора ряд $\xi (x-R/2)+\xi (x+R/2)$ является:

$(16{\sqrt {5}})/25-(x/R)^{4}(2304{\sqrt {5}})/3125+{\mathcal {O}}((x/R)^{6})\approx 1.43-1.65(x/R)^{4}+{\mathcal {O}}((x/R)^{6})$ .

В антигельмгольцевой паре напряженность B-поля при любом $x$ будет:

{\begin{aligned}B(x)&={\frac {\mu _{0}nI}{2R}}\left[\xi (x-R/2)-\xi (x+R/2)\right]\\&={\frac {\mu _{0}nI}{2R}}\left([1+(x/R-1/2)^{2}]^{-3/2}-[1+(x/R+1/2)^{2}]^{-3/2}\right)\\\end{aligned}}

Точки рядом с центром (на полпути между двумя катушками) имеют $x\ll R$ и ряд Тейлора $\xi (x-R/2)-\xi (x+R/2)$ является:

$(x/R)(96{\sqrt {5}})/125-(x/R)^{3}(512{\sqrt {5}})/625+{\mathcal {O}}((x/R)^{5})\approx 1.72(x/R)-1.83(x/R)^{3}+{\mathcal {O}}((x/R)^{5})$ .

Изменяющееся во времени магнитное поле

Большинство катушек Гельмгольца используют постоянный (постоянный) ток для создания статического магнитного поля. Многие приложения и эксперименты требуют изменяющегося во времени магнитного поля. Эти приложения включают тесты на чувствительность к магнитному полю, научные эксперименты и биомедицинские исследования (взаимодействие между магнитным полем и живой тканью). Требуемые магнитные поля обычно имеют импульсную или непрерывную синусоидальную форму. Диапазон частот магнитного поля может варьироваться от постоянного тока (0 Гц) до многих килогерц или даже мегагерц (МГц). Для создания необходимого изменяющегося во времени магнитного поля необходим драйвер катушки Гельмгольца переменного тока. Драйвер усилителя сигнала должен быть способен выдавать высокий переменный ток для создания магнитного поля.

Напряжение и ток драйвера

$I=\left({\frac {5}{4}}\right)^{3/2}\left({\frac {BR}{\mu _{0}n}}\right)$

Используйте приведенное выше уравнение в разделе математики, чтобы рассчитать ток катушки для желаемого магнитного поля $B$ .

где $\mu _{0}$ это проницаемость свободного пространства или $4\pi \times 10^{-7}{\text{ T}}\cdot {\text{m/A}}=1.257\times 10^{-6}{\text{ T}}\cdot {\text{m/A}},$

$I\;$ = ток катушки, в амперах,

$R\;$ = радиус катушки, в метрах,

n = количество витков в каждой катушке.

Использование функционального генератора и сильноточного усилителя сигнала для генерации высокочастотного магнитного поля Гельмгольца.

Затем рассчитайте необходимое напряжение усилителя драйвера катушки Гельмгольца: ^[6]

V=I{\sqrt {{\bigl [}\omega {\bigl (}L_{1}+L_{2}{\bigr )}{\bigr ]}^{2}+{\bigl (}R_{1}+R_{2}{\bigr )}^{2}}}

где

$I$ – пиковый ток,
$ω$ — угловая частота или $ω = 2 πf$ ,
$L 1$ и $L 2$ — индуктивности двух катушек Гельмгольца, а
$R 1$ и $R 2$ — сопротивления двух катушек.

Высокочастотный последовательный резонансный

Создать статическое магнитное поле относительно легко; сила поля пропорциональна току. Создание высокочастотного магнитного поля является более сложной задачей. Катушки являются индукторами, и их сопротивление увеличивается пропорционально частоте. Чтобы обеспечить ту же напряженность поля при удвоенной частоте, требуется удвоенное напряжение на катушке. Вместо прямого возбуждения катушки высоким напряжением для обеспечения высокого напряжения можно использовать последовательный резонансный контур. ^[7] Последовательно с катушками включен последовательный конденсатор. Емкость подбирается так, чтобы катушка резонировала на нужной частоте. Остается только паразитное сопротивление катушек. Этот метод работает только на частотах, близких к резонансной частоте; для генерации поля на других частотах требуются другие конденсаторы. Резонансная частота катушки Гельмгольца, $f_{0}$ и номинал конденсатора C приведены ниже. ^[6]

f_{0}={\frac {1}{2\pi {\sqrt {\left(L_{1}+L_{2}\right)C}}}}

C={\frac {1}{\left(2\pi f_{0}\right)^{2}\left(L_{1}+L_{2}\right)}}

Катушки Максвелла

Чтобы улучшить однородность поля в пространстве внутри катушек, снаружи можно добавить дополнительные катушки. Джеймс Клерк Максвелл показал в 1873 году, что третья катушка большего диаметра расположена посередине между двумя катушками Гельмгольца, при этом расстояние между катушками увеличивается по мере увеличения радиуса катушки. $R$ к ${\sqrt {3}}R$ может свести дисперсию поля на оси к нулю вплоть до шестой производной положения. Иногда ее называют катушкой Максвелла .

См. также

Соленоид
Массив Хальбаха
Магнитная бутылка имеет ту же структуру, что и катушки Гельмгольца, но магниты разнесены дальше друг от друга, так что поле расширяется посередине, захватывая заряженные частицы расходящимися силовыми линиями. Если одну катушку перевернуть, образуется ловушка возврата , которая также улавливает заряженные частицы. ^[8]
Катушки Гельмгольца были спроектированы и изготовлены для лаборатории испытаний электромагнитных композитов Армейской исследовательской лаборатории в 1993 году для испытаний композитных материалов в низкочастотных магнитных полях. ^[9]

Ссылки

^ Рамсден, Эдвард (2006). Датчики Холла: теория и приложения (2-е изд.). Амстердам: Эльзевир/Ньюнес. п. 195. ИСБН 978-0-75067934-3 .
↑ Катушка Гельмгольца в устройствах CGS. Архивировано 24 марта 2012 г. в Wayback Machine.
^ «Электромагнетизм» . Архивировано из оригинала 3 июня 2011 г. Проверено 20 ноября 2007 г.
^ «Магнетометр поля Земли: катушка Гельмгольца» Ричарда Вотиза, 2004 г. Архивировано 28 июня 2007 г., archive.today .
^ «Магнитное поле токовой петли» .
^ Jump up to: ^а ^б Ян, КЦ. «Высокочастотные катушки Гельмгольца генерируют магнитные поля» . ЭДН . Проверено 27 января 2016 г.
^ «Высокочастотная резонансная электромагнитная катушка» . www.accelinstruments.com . Проверено 25 февраля 2016 г.
^ «Вход — группа АСАКУСА МУСАСИ» .
^ Дж., ДеТрой, Дэвид; Дж. Чейз, Рональд (ноябрь 1994 г.). «Расчет и измерение полей катушки Гельмгольца» . Архивировано из оригинала 2 июня 2018 года. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) CS1 maint: несколько имен: список авторов ( ссылка )

Внешние ссылки

Осевое поле идеальной катушки Гельмгольца
Осевое поле реальной пары катушек Гельмгольца
Поля катушек Гельмгольца, автор Франц Крафт, Демонстрационный проект Вольфрама .
Кевин Кунс (2007) «Расчет магнитного поля внутри плазменной камеры » использует эллиптические интегралы и их производные для расчета внеосевых полей, из PBworks .
ДеТрой, Дэвид Дж.; Чейз, Рональд Дж. (ноябрь 1994 г.), Расчет и измерение полей катушек Гельмгольца (PDF) , Армейская исследовательская лаборатория, ARL-TN-35, заархивировано (PDF) из оригинала 18 апреля 2013 г.
Магнитные поля катушек. Архивировано 30 апреля 2015 г. в Wayback Machine.
http://physicsx.pr.erau.edu/HelmholtzCoils/

[1] Рамсден, Эдвард (2006). Датчики Холла: теория и приложения (2-е изд.). Амстердам: Эльзевир/Ньюнес. п. 195. ИСБН 978-0-75067934-3 .

[2] Катушка Гельмгольца в устройствах CGS. Архивировано 24 марта 2012 г. в Wayback Machine.

[3] «Электромагнетизм» . Архивировано из оригинала 3 июня 2011 г. Проверено 20 ноября 2007 г.

[4] «Магнетометр поля Земли: катушка Гельмгольца» Ричарда Вотиза, 2004 г. Архивировано 28 июня 2007 г., archive.today .

[5] «Магнитное поле токовой петли» .

[:0-6] Jump up to: ^а ^б Ян, КЦ. «Высокочастотные катушки Гельмгольца генерируют магнитные поля» . ЭДН . Проверено 27 января 2016 г.

[7] «Высокочастотная резонансная электромагнитная катушка» . www.accelinstruments.com . Проверено 25 февраля 2016 г.

[8] «Вход — группа АСАКУСА МУСАСИ» .

[9] Дж., ДеТрой, Дэвид; Дж. Чейз, Рональд (ноябрь 1994 г.). «Расчет и измерение полей катушки Гельмгольца» . Архивировано из оригинала 2 июня 2018 года. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) CS1 maint: несколько имен: список авторов ( ссылка )

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]