Вычисление проверок циклическим избыточным кодом

Вычисление проверки циклическим избыточным кодом основано на математическом делении полинома по модулю два . На практике это похоже на длинное деление строки двоичного сообщения с добавленным фиксированным количеством нулей на строку «полинома генератора», за исключением того, что исключающие операции или операции заменяют вычитания. Деление этого типа эффективно реализуется аппаратно с помощью модифицированного сдвигового регистра . ^[1] и в программном обеспечении с помощью ряда эквивалентных алгоритмов , начиная с простого кода, близкого к математике, и становясь более быстрым (и, возможно, более запутанным). ^[2]) посредством побайтового компромисса между пространством и параллелизма и временем .

Пример генерации 8-битной CRC . Генератор представляет собой сдвиговый регистр типа Галуа с логическими элементами XOR, расположенными в соответствии со степенями (белыми числами) x в полиноме генератора. Поток сообщений может быть любой длины. После того, как он был пропущен через регистр, за которым следуют 8 нулей, результатом в регистре является контрольная сумма.

Проверка полученных данных по контрольной сумме. Полученное сообщение сдвигается через тот же регистр, который используется в генераторе, но к нему вместо нулей присоединяется полученная контрольная сумма. Правильные данные дают результат, состоящий из всех нулей; поврежденный бит в сообщении или контрольной сумме даст другой результат, предупреждая о том, что произошла ошибка.

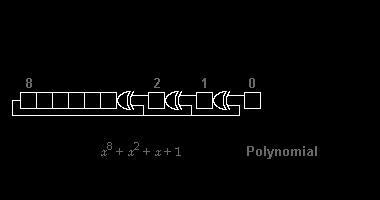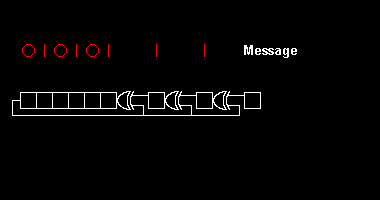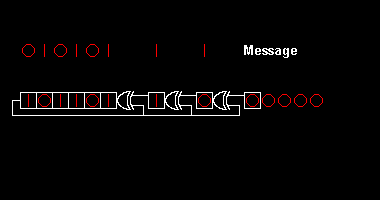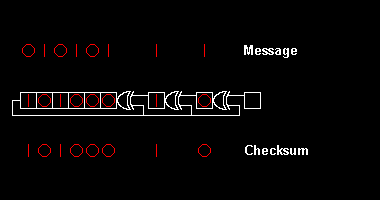
Различные стандарты CRC расширяют алгоритм полиномиального деления, определяя начальное значение регистра сдвига, последний шаг «исключающее ИЛИ» и, что наиболее важно, порядок битов ( порядок байтов ). В результате код, видимый на практике, отклоняется от «чистого» деления. ^[2] и регистр может сдвигаться влево или вправо.

Пример

В качестве примера аппаратной реализации полиномиального деления предположим, что мы пытаемся вычислить 8-битную CRC 8-битного сообщения, состоящего из символа ASCII «W», который является двоичным 01010111 ₂ , десятичным 87 ₁₀ или шестнадцатеричным 57. ₁₆ . Для иллюстрации мы будем использовать полином CRC-8-ATM ( HEC ). $x^{8}+x^{2}+x+1$ . Запись первого переданного бита (коэффициент старшей степени $x$ ) слева это соответствует 9-битной строке «100000111».

Значение байта 57 ₁₆ может передаваться в двух разных порядках, в зависимости от используемого соглашения о порядке битов. Каждый из них генерирует свой полином сообщения. $M(x)$ . Msbit-во-первых, это $x^{6}+x^{4}+x^{2}+x+1$ = 01010111, а lsbit-first, это $x^{7}+x^{6}+x^{5}+x^{3}+x$ = 11101010. Затем их можно умножить на $x^{8}$ создать два 16-битных полинома сообщения $x^{8}M(x)$ .

Тогда вычисление остатка состоит из вычитания кратных полинома генератора. $G(x)$ . Это похоже на деление десятичной дроби, но даже проще, поскольку на каждом шаге единственными возможными кратными являются 0 и 1, а вычитания заимствуются «из бесконечности», а не уменьшают старшие цифры. Поскольку нас не волнует частное, нет необходимости его записывать.

Самый значимый бит первый

Младший бит первым

	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
−	0	0	0	0	0	0	0	0	0
=	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
		−	0	0	0	0	0	0	0	0	0
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
			−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
				−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
					−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	1	0	1	0	1	0	1	1	0	0
						−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0

	1	1	1	0	1	0	1	0	0	0	0	0	0	0	0	0
−	1	0	0	0	0	0	1	1	1
=	0	1	1	0	1	0	0	1	1	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0
		−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
			−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
				−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
					−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
						−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0

Обратите внимание, что после каждого вычитания биты делятся на три группы: вначале группа, состоящая только из нулей; в конце группа, не отличающаяся от оригинала; и группа с синей заливкой посередине, что «интересно». «Интересная» группа имеет длину 8 бит, что соответствует степени полинома. На каждом шаге соответствующее кратное многочлена вычитается, чтобы сделать нулевую группу на один бит длиннее, а неизмененная группа становится на один бит короче, пока не останется только последний остаток.

В примере msbit-first полином остатка равен $x^{7}+x^{5}+x$ . Преобразование в шестнадцатеричное число с использованием соглашения, согласно которому наивысшая степень x равна мсбиту; это А2 ₁₆ . В lsbit-first остаток равен $x^{7}+x^{4}+x^{3}$ . Преобразование в шестнадцатеричный формат с использованием соглашения о том, что наивысшая степень x — это lsbit, это 19 ₁₆ .

Выполнение

Записывать полное сообщение на каждом этапе, как это сделано в примере выше, очень утомительно. Эффективные реализациииспользовать $n$ -битовый сдвиговый регистр для хранения только интересных битов. Умножив полином на $x$ эквивалентно сдвигу регистра на одну позицию, поскольку коэффициенты не изменяются по значению, а лишь перемещаются к следующему члену многочлена.

Вот первый вариант псевдокода для вычисления n -битной CRC. Он использует надуманный составной тип данных для полиномов, где x — это не целочисленная переменная, а конструктор, генерирующий полиномиальный объект , который можно складывать, умножать и возводить в степень. К xor двух многочленов – это сложить их по модулю два; то есть исключающее ИЛИ коэффициенты каждого совпадающего термина из обоих полиномов.

function crc(bit array bitString[1..len], int len) {    remainderPolynomial := polynomialForm(bitString[1..n])   // First n bits of the message    // A popular variant complements remainderPolynomial here; see § Preset to −1 below    for i from 1 to len {        remainderPolynomial := remainderPolynomial * x + bitString[i+n] * x⁰   // Define bitString[k]=0 for k>len        if coefficient of xⁿ of remainderPolynomial = 1 {            remainderPolynomial := remainderPolynomial xor generatorPolynomial        }    }    // A popular variant complements remainderPolynomial here; see § Post-invert below    return remainderPolynomial}

Фрагмент кода 1: Простое полиномиальное деление

Обратите внимание, что в этом примере кода не требуется указывать соглашение о порядке битов, поскольку не используются байты; вход bitString уже находится в виде битового массива, а remainderPolynomial манипулируется с помощью полиномиальных операций; умножение на $x$ может быть сдвигом влево или вправо, а также добавлением bitString[i+n] делается для $x^{0}$ коэффициент, который может быть правым или левым концом регистра.

Этот код имеет два недостатка. Во-первых, на самом деле требуется n +1-битный регистр для хранения remainderPolynomial так что $x^{n}$ коэффициент можно проверить. Что еще более важно, это требует bitString быть дополнено n нулевыми битами.

Первую проблему можно решить, протестировав $x^{n-1}$ коэффициент remainderPolynomial прежде чем оно будет умножено на $x$ .

Вторую проблему можно было бы решить, выполнив последние n итераций иначе, но существует более тонкая оптимизация, которая используется повсеместно как в аппаратных, так и в программных реализациях.

Поскольку операция XOR, используемая для вычитания полинома генератора из сообщения, является коммутативной и ассоциативной , не имеет значения, в каком порядке различные входные данные объединяются в remainderPolynomial. И, в частности, определенный фрагмент bitString не нужно добавлять в remainderPolynomial до самого последнего момента, когда он проверяется, стоит ли xor с generatorPolynomial.

Это устраняет необходимость предварительной загрузки remainderPolynomial также с первыми n битами сообщения:

function crc(bit array bitString[1..len], int len) {    remainderPolynomial := 0    // A popular variant complements remainderPolynomial here; see § Preset to −1 below    for i from 1 to len {        remainderPolynomial := remainderPolynomial xor (bitstring[i] * xⁿ⁻¹)        if (coefficient of xⁿ⁻¹ of remainderPolynomial) = 1 {            remainderPolynomial := (remainderPolynomial * x) xor generatorPolynomial        } else {            remainderPolynomial := (remainderPolynomial * x)        }    }    // A popular variant complements remainderPolynomial here; see § Post-invert below    return remainderPolynomial}

Фрагмент кода 2: Полиномиальное деление с отложенным XOR-сообщением

Это стандартная побитовая аппаратная реализация CRC, достойная изучения; как только вы поймете, почему это вычисляет точно такой же результат, как и первая версия, остальные оптимизации станут довольно простыми. Если remainderPolynomial имеет длину всего n бит, то $x^{n}$ коэффициенты его и generatorPolynomial просто отбрасываются. По этой причине вы обычно увидите полиномы CRC, записанные в двоичном формате с опущенным старшим коэффициентом.

В программном обеспечении удобно отметить, что, хотя можно и отложить xor каждого бита до самого последнего момента, можно сделать это и раньше. Обычно удобно выполнять xor побайтно : , даже в такой побитовой реализации

function crc(byte array string[1..len], int len) {    remainderPolynomial := 0    // A popular variant complements remainderPolynomial here; see § Preset to −1 below    for i from 1 to len {        remainderPolynomial := remainderPolynomial xor polynomialForm(string[i]) * xⁿ⁻⁸        for j from 1 to 8 {    // Assuming 8 bits per byte            if coefficient of xⁿ⁻¹ of remainderPolynomial = 1 {                remainderPolynomial := (remainderPolynomial * x) xor generatorPolynomial            } else {                remainderPolynomial := (remainderPolynomial * x)            }        }    }    // A popular variant complements remainderPolynomial here; see § Post-invert below    return remainderPolynomial}

Фрагмент кода 3: Полиномиальное деление с побайтовым исключающим ИЛИ сообщений

Обычно это самая компактная программная реализация, используемая в микроконтроллерах , когда пространство важнее скорости.

Порядок битов (endianness)

При реализации в с последовательным битом аппаратном обеспечении полином генератора однозначно описывает назначение битов; первый передаваемый бит всегда является коэффициентом высшей степени $x$ и последний $n$ передаваемые биты представляют собой остаток CRC $R(x)$ , начиная с коэффициента $x^{n-1}$ и заканчивая коэффициентом $x^{0}$ , он же коэффициент 1.

Однако, когда биты обрабатываются побайтно , например, при использовании параллельной передачи , кадрировании байтов, как при кодировании 8B/10B или RS-232 в стиле асинхронной последовательной связи , или при реализации CRC в программном обеспечении , необходимо указать порядок битов (порядок байтов) данных; какой бит в каждом байте считается «первым» и будет коэффициентом высшей степени $x$ .

Если данные предназначены для последовательной связи , лучше всего использовать порядок битов, в котором данные будут в конечном итоге отправлены. Это связано с тем, что способность CRC обнаруживать пакетные ошибки основана на близости полинома сообщения. $M(x)$ ; если соседние полиномиальные члены не передаются последовательно, пакет физических ошибок одной длины может рассматриваться как более длинный пакет из-за перестановки битов.

Например, стандарты IEEE 802 ( Ethernet ) и RS-232 ( последовательный порт ) определяют передачу сначала младшего значащего бита (с прямым порядком байтов), поэтому программная реализация CRC для защиты данных, передаваемых по такому каналу, должна отображать младшие биты. в каждом байте к коэффициентам высших степеней $x$ . С другой стороны, дискеты и большинство жестких дисков сначала записывают старший бит каждого байта.

CRC lsbit-first немного проще реализовать в программном обеспечении, поэтому он встречается несколько чаще, но многие программисты находят, что порядок битов msbit-first легче соблюдать. Так, например, расширение XMODEM -CRC, раннее использование CRC в программном обеспечении, использует CRC с приоритетом мсбита.

До сих пор псевдокод избегал указания порядка битов внутри байтов, описывая сдвиги в псевдокоде как умножения на $x$ и написание явных преобразований из двоичной формы в полиномиальную. На практике CRC хранится в стандартном двоичном регистре с использованием определенного соглашения о порядке битов. В форме «сначала msbit» наиболее значимые двоичные биты будут отправлены первыми и, таким образом, содержат полиномиальные коэффициенты более высокого порядка, тогда как в форме «сначала lsbit» младшие двоичные биты содержат коэффициенты более высокого порядка. Приведенный выше псевдокод можно записать в обеих формах. Для конкретности здесь используется 16-битный CRC-16- CCITT. полином $x^{16}+x^{12}+x^{5}+1$ :

// Most significant bit first (big-endian)// (x¹⁶)+x¹²+x⁵+1 = (1) 0001 0000 0010 0001 = 0x1021function crc(byte array string[1..len], int len) {    rem := 0    // A popular variant complements rem here    for i from 1 to len {        rem  := rem xor (string[i] leftShift (n-8))   // n = 16 in this example        for j from 1 to 8 {       // Assuming 8 bits per byte            if rem and 0x8000 {   // Test x¹⁵ coefficient                rem  := (rem leftShift 1) xor 0x1021            } else {                rem  := rem leftShift 1            }            rem  := rem and 0xffff      // Trim remainder to 16 bits        }    }    // A popular variant complements rem here    return rem}

Фрагмент кода 4: Деление на основе сдвигового регистра, сначала старший бит.

// Least significant bit first (little-endian)// 1+x⁵+x¹²+(x¹⁶) = 1000 0100 0000 1000 (1) = 0x8408function crc(byte array string[1..len], int len) {    rem  := 0    // A popular variant complements rem here    for i from 1 to len {        rem  := rem xor string[i]        for j from 1 to 8 {       // Assuming 8 bits per byte            if rem and 0x0001 {   // Test x¹⁵ coefficient                rem  := (rem rightShift 1) xor 0x8408            } else {                rem  := rem rightShift 1            }        }    }    // A popular variant complements rem here    return rem}

Фрагмент кода 5: Деление на основе сдвигового регистра, сначала младший бит.

Обратите внимание, что форма lsbit-first позволяет избежать необходимости сдвига string[i] перед xor. В любом случае обязательно передавайте байты CRC в том порядке, который соответствует выбранному вами соглашению о порядке битов.

Многобитные вычисления

Алгоритм Сарвате (одна таблица поиска)

Другая распространенная оптимизация использует справочную таблицу, индексированную коэффициентами высшего порядка rem обрабатывать более одного бита дивиденда за итерацию. ^[3] Чаще всего используется таблица поиска из 256 записей, заменяющая тело внешнего цикла (через i) с:

// Msbit-firstrem = (rem leftShift 8) xor big_endian_table[string[i] xor ((leftmost 8 bits of rem) rightShift (n-8))]// Lsbit-firstrem = (rem rightShift 8) xor little_endian_table[string[i] xor (rightmost 8 bits of rem)]

Фрагмент кода 6: Ядра табличного деления

Один из наиболее часто встречающихся алгоритмов CRC известен как CRC-32 , используемый (среди прочих) Ethernet , FDDI , ZIP и другими форматами архивов , а также PNG форматом изображений . Его полином может быть записан с приоритетом msbit как 0x04C11DB7 или lsbit-first как 0xEDB88320. Веб-страница W3C в формате PNG включает приложение с короткой и простой табличной реализацией CRC-32 на языке C. ^[4] Вы заметите, что код соответствует представленному здесь псевдокоду lsbit-first побайтно, а таблица генерируется с использованием побитового кода.

Использование таблицы на 256 записей обычно наиболее удобно, но можно использовать и другие размеры. В небольших микроконтроллерах использование таблицы из 16 записей для одновременной обработки четырех бит дает существенное повышение скорости, сохраняя при этом размер таблицы. На компьютерах с достаточным объемом памяти таблица из 65 536 записей может использоваться для обработки 16 бит за раз.

Создание таблиц

Программное обеспечение для создания таблиц настолько маленькое и быстрое, что обычно быстрее вычислить их при запуске программы, чем загружать предварительно рассчитанные таблицы из хранилища. Одним из популярных методов является использование побитового кода 256 раз для генерации CRC 256 возможных 8-битных байтов. Однако это можно существенно оптимизировать, воспользовавшись свойством, которое table[i xor j] == table[i] xor table[j]. Непосредственно вычисляются только записи таблицы, соответствующие степеням двойки.

В следующем примере кода crc имеет значение table[i]:

big_endian_table[0] := 0crc := 0x8000 // Assuming a 16-bit polynomiali := 1do {    if crc and 0x8000 {        crc := (crc leftShift 1) xor 0x1021 // The CRC polynomial    } else {        crc := crc leftShift 1    }    // crc is the value of big_endian_table[i]; let j iterate over the already-initialized entries    for j from 0 to i−1 {        big_endian_table[i + j] := crc xor big_endian_table[j];    }    i := i leftshift 1} while i < 256

Фрагмент кода 7: Побайтовая генерация таблицы CRC, сначала старший бит.

little_endian_table[0] := 0crc := 1;i := 128do {    if crc and 1 {        crc := (crc rightShift 1) xor 0x8408 // The CRC polynomial    } else {        crc := crc rightShift 1    }    // crc is the value of little_endian_table[i]; let j iterate over the already-initialized entries    for j from 0 to 255 by 2 × i {        little_endian_table[i + j] := crc xor little_endian_table[j];    }    i := i rightshift 1} while i > 0

Фрагмент кода 8: Побайтовая генерация таблицы CRC, сначала младший бит.

В этих примерах кода индекс таблицы i + j эквивалентно i xor j; вы можете использовать любую форму, которая вам удобнее.

Алгоритм CRC-32

Это практический алгоритм для варианта CRC-32. ^[5] CRCTable — это мемоизация вычислений, которые необходимо будет повторять для каждого байта сообщения ( Вычисление проверок циклическим избыточным кодом § Многобитовые вычисления ).

Function CRC32   Input:      data:  Bytes     // Array of bytes   Output:      crc32: UInt32    // 32-bit unsigned CRC-32 value
// Initialize CRC-32 to starting valuecrc32 ← 0xFFFFFFFF
for each byte in data do   nLookupIndex ← (crc32 xor byte) and 0xFF   crc32 ← (crc32 shr 8) xor CRCTable[nLookupIndex]  // CRCTable is an array of 256 32-bit constants
// Finalize the CRC-32 value by inverting all the bitscrc32 ← crc32 xor 0xFFFFFFFFreturn crc32

В C алгоритм выглядит так:

#include <inttypes.h> // uint32_t, uint8_tuint32_t CRC32(const uint8_t data[], size_t data_length) {	uint32_t crc32 = 0xFFFFFFFFu;		for (size_t i = 0; i < data_length; i++) {		const uint32_t lookupIndex = (crc32 ^ data[i]) & 0xff;		crc32 = (crc32 >> 8) ^ CRCTable[lookupIndex];  // CRCTable is an array of 256 32-bit constants	}		// Finalize the CRC-32 value by inverting all the bits	crc32 ^= 0xFFFFFFFFu;	return crc32;}

Нарезка байтов с использованием нескольких таблиц

Существует алгоритм среза на n (обычно срез на 8 для CRC32), который обычно удваивает или утраивает производительность по сравнению с алгоритмом Сарвате. Вместо чтения по 8 бит за раз алгоритм читает 8 n бит за раз. Это максимизирует производительность суперскалярных процессоров. ^[6]^[7]^[8]^[9]

Неясно, кто на самом деле изобрел алгоритм. ^[10]

Чтобы понять преимущества, начните со случая среза на 2. Мы хотим вычислить CRC по 2 байта (16 бит) за раз, но стандартный табличный подход потребует неудобно большой таблицы из 65536 записей. Как упоминалось в разделе «Генерация таблиц» , таблицы CRC обладают свойством, которое table[i xor j] = table[i] xor table[j]. Мы можем использовать этот идентификатор, чтобы заменить большую таблицу двумя таблицами по 256 записей: table[i + 256×j] = table_low[i] xor table_high[j].

Таким образом, большая таблица не сохраняется явно, но на каждой итерации вычисляется значение CRC, которое будет там, путем объединения значений в двух меньших таблицах. То есть 16-битный индекс «разрезается» на два 8-битных индекса. На первый взгляд это кажется бессмысленным; зачем выполнять два поиска в отдельных таблицах, если стандартный побайтовый алгоритм выполняет два поиска в одной и той же таблице?

Разница заключается в параллелизме на уровне инструкций . В стандартном алгоритме индекс для каждого поиска зависит от значения, полученного в предыдущем. Таким образом, второй поиск не может начаться, пока не завершится первый поиск.

При использовании срезированных таблиц оба поиска могут начинаться одновременно. Если процессор сможет выполнять две нагрузки параллельно (микропроцессоры 2020-х годов могут отслеживать более 100 выполняемых загрузок), то это потенциально может удвоить скорость внутреннего цикла.

Очевидно, что этот метод можно распространить на столько срезов, сколько процессор может извлечь из этого выгоду.

Когда ширина среза равна размеру CRC, происходит незначительное ускорение. В той части базового алгоритма Сарвате, где предыдущее значение CRC сдвигается на размер поиска в таблице, предыдущее значение CRC полностью смещается (все, что остается, — это ноль), поэтому XOR можно исключить из критического пути.

Результирующий внутренний цикл среза на n состоит из:

XOR текущая CRC со следующими n байтами сообщения,
найдите каждый байт результирующего значения в n таблицах срезов, затем
XOR n результатов, чтобы получить следующий CRC.

Это по-прежнему имеет то свойство, что все загрузки на втором этапе должны быть завершены до начала следующей итерации, что приводит к регулярным паузам, во время которых подсистема памяти процессора (в частности, кэш данных) не используется. Однако когда ширина среза превышает размер CRC, появляется значительное второе ускорение.

Это связано с тем, что часть результатов первого шага больше не зависит от какой-либо предыдущей итерации. При выполнении XOR 32-битной CRC с 64-битным сообщением половина результата представляет собой просто копию сообщения. При тщательном кодировании (во избежание создания ложной зависимости данных ) половина загрузки таблицы срезов может начаться до завершения предыдущей итерации цикла. занятость подсистемы памяти процессора В результате получается достаточно работы, чтобы поддерживать постоянную , что обеспечивает максимальную производительность. Как уже упоминалось, в микропроцессорах, выпущенных после 2000 года, для достижения этого уровня обычно достаточно среза на 8.

Нет особой необходимости в том, чтобы срезы имели ширину 8 бит. Например, было бы вполне возможно вычислить CRC по 64 бита за раз, используя алгоритм среза по 9, используя 9 справочных таблиц по 128 записей для обработки 63 битов, а 64-й бит обрабатывается побитовым алгоритмом. -временной алгоритм (который фактически представляет собой 1-битную справочную таблицу с 2 записями). Это почти вдвое уменьшит размер таблицы (с 8×256 = 2048 записей до 9×128 = 1152) за счет еще одной загрузки, зависящей от данных, на итерацию.

Параллельные вычисления без таблицы

Параллельное обновление побайта или слова также можно выполнить явно, без таблицы. ^[11] Обычно это используется в высокоскоростных аппаратных реализациях. Для каждого бита уравнение решается после сдвига 8 бит. В следующих таблицах перечислены уравнения для некоторых часто используемых полиномов с использованием следующих символов:

c_Там	Бит CRC 7…0 (или 15…0) перед обновлением
р _я	Бит CRC 7…0 (или 15…0) после обновления
d_Из	бит входных данных 7…0
и _я = d _я + c _я	e _p = e ₇ + e ₆ + … + e ₁ + e ₀ (parity bit)
s _я = d _я + c _я+8	s _p = s ₇ + s ₆ + … + s ₁ + s ₀ (бит четности)

Уравнения побитового обновления для некоторых полиномов CRC-8 после сдвига 8 бит
Полином:	( х ⁷ + х ³ + 1) × x (CRC-7-CCITT со сдвигом влево)	х ⁸ + х ⁵ + х ⁴ + 1 (CRC-8-Даллас/Максим)
Коэффициенты:	0x12 = (0x09 << 1) ( MSBF /нормальный)	0x8c ( LSBF /обратный)
r₀ ←r₁ ←r₂ ←r₃ ←r₄ ←r₅ ←r₆ ←r₇ ←	0e₀ + e₄ + e₇e₁ + e₅e₂ + e₆e₃ + e₇ + e₀ + e₄ + e₇e₄ + e₁ + e₅e₅ + e₂ + e₆e₆ + e₃ + e₇	e₀ + e₄ + e₁ + e₀ + e₅ + e₂ + e₁e₁ + e₅ + e₂ + e₁ + e₆ + e₃ + e₂ + e₀e₂ + e₆ + e₃ + e₂ + e₀ + e₇ + e₄ + e₃ + e₁e₃ + e₀ + e₇ + e₄ + e₃ + e₁e₄ + e₁ + e₀e₅ + e₂ + e₁e₆ + e₃ + e₂ + e₀e₇ + e₄ + e₃ + e₁
C-код фрагменты:	uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e >> 4) ^ (e >> 7); r = (f << 1) ^ (f << 4);	uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e << 3) ^ (e << 4) ^ (e << 6); r = f ^ (f >> 4) ^ (f >> 5);

Уравнения побитового обновления для некоторых полиномов CRC-16 после сдвига 8 бит
Полином:	х ¹⁶ + х ¹² + х ⁵ + 1 (CRC-16-CCITT)		х ¹⁶ + х ¹⁵ + х ² +1 (CRC-16-ANSI)
Коэффициенты:	0x1021 (MSBF/нормальный)	0x8408 (LSBF/реверс)	0x8005 (MSBF/нормальный)	0xa001 (LSBF/реверс)
r₀ ←r₁ ←r₂ ←r₃ ←r₄ ←r₅ ←r₆ ←r₇ ←r₈ ←r₉ ←r₁₀ ←r₁₁ ←r₁₂ ←r₁₃ ←r₁₄ ←r₁₅ ←	s₄ + s₀s₅ + s₁s₆ + s₂s₇ + s₃ s₄ s₅ + s₄ + s₀ s₆ + s₅ + s₁ s₇ + s₆ + s₂c₀ + s₇ + s₃c₁ + s₄c₂ + s₅c₃ + s₆c₄ + s₇ + s₄ + s₀c₅ + s₅ + s₁c₆ + s₆ + s₂c₇ + s₇ + s₃	c₈ + e₄ + e₀c₉ + e₅ + e₁c₁₀ + e₆ + e₂c₁₁ + e₀ + e₇ + e₃c₁₂ + e₁c₁₃ + e₂c₁₄ + e₃c₁₅ + e₄ + e₀ e₀ + e₅ + e₁ e₁ + e₆ + e₂ e₂ + e₇ + e₃ e₃ e₄ + e₀ e₅ + e₁ e₆ + e₂ e₇ + e₃	s_p s₀ + s_p s₁ + s₀ s₂ + s₁ s₃ + s₂ s₄ + s₃ s₅ + s₄ s₆ + s₅c₀ + s₇ + s₆c₁ + s₇c₂c₃c₄c₅c₆c₇ + s_p	c₈ + e_pc₉c₁₀c₁₁c₁₂c₁₃c₁₄ + e₀c₁₅ + e₁ + e₀ e₂ + e₁ e₃ + e₂ e₄ + e₃ e₅ + e₄ e₆ + e₅ e₇ + e₆ e_p + e₇ e_p
C-код фрагменты:	uint8_t d, s, t; uint16_t c, r; … s = d ^ (c >> 8); t = s ^ (s >> 4); r = (c << 8) ^ t ^ (t << 5) ^ (t << 12);	uint8_t d, e, f; uint16_t c, r; … e = c ^ d; f = e ^ (e << 4); r = (c >> 8) ^ (f << 8) ^ (f << 3) ^ (f >> 4);	uint8_t d, s, p; uint16_t c, r, t; … s = d ^ (c >> 8); p = s ^ (s >> 4); p = p ^ (p >> 2); p = p ^ (p >> 1); p = p & 1; t = p \| (s << 1); r = (c << 8) ^ (t << 15) ^ t ^ (t << 1);	uint8_t d, e, p; uint16_t c, r, f; … e = c ^ d; p = e ^ (e >> 4); p = p ^ (p >> 2); p = p ^ (p >> 1); p = p & 1; f = e \| (p << 8); r = (c >> 8) ^ (f << 6) ^ (f << 7) ^ (f >> 8);

Двухэтапное вычисление

Поскольку полином CRC-32 имеет большое количество членов, при вычислении остатка побайтно каждый бит зависит от 8 бит предыдущей итерации. В аппаратных реализациях с байтовым параллелизмом это требует использования либо 8-входовых, либо каскадных вентилей XOR, что увеличивает задержку распространения .

Чтобы максимизировать скорость вычислений, промежуточный остаток можно вычислить, сначала вычислив CRC сообщения по модулю x. ¹²³ + х ¹¹¹ + х ⁹² + х ⁸⁴ + х ⁶⁴ + х ⁴⁶ + х ²³ + 1. Это тщательно выбранное кратное полиному CRC-32, такое, что члены (отводы обратной связи) находятся на расстоянии не менее 8 позиций друг от друга. Таким образом, 123-битный сдвиговый регистр можно расширить на 8 бит за итерацию, используя только двухвходовые логические элементы XOR, что является максимально быстрым. Наконец, промежуточный остаток можно уменьшить по модулю стандартного полинома во втором сдвиговом регистре, чтобы получить остаток CRC-32. ^[12]

Если разрешены вентили XOR с 3 или 4 входами, можно использовать более короткие промежуточные полиномы степени 71 или 53 соответственно.

Блочные вычисления

Блочное вычисление остатка может быть выполнено аппаратно для любого полинома CRC путем факторизации матрицы преобразования пространства состояний, необходимой для вычисления остатка, на две более простые матрицы Теплица. ^[13]

Однопроходная проверка

При добавлении CRC к сообщению можно отделить переданный CRC, пересчитать его и сверить перевычисленное значение с переданным. Однако обычно используется более простой метод.используется в аппаратном обеспечении.

Когда CRC передается с правильным порядком байтов (соответствующим выбранному соглашению о порядке битов), получатель может вычислить общий CRC для сообщения и CRC, и если они верны, результат будет нулевым. ^[14]Эта возможность является причиной того, что большинство сетевых протоколов, включающих CRC, делают это перед конечным разделителем; для проверки CRC не обязательно знать, близок ли конец пакета.

Фактически, некоторые протоколы используют CRC в качестве разделителя сообщений — метод, называемый кадрированием на основе CRC . (Для этого требуется несколько кадров для обнаружения захвата или потери кадра, поэтому он ограничен приложениями, в которых кадры имеют известную длину, а содержимое кадра достаточно случайно, поэтому действительные CRC в невыровненных данных встречаются редко.)

Варианты CRC

На практике большинство стандартов предписывают установку регистра на все единицы и инвертирование CRC перед передачей. Это не влияет на способность CRC обнаруживать измененные биты, но дает возможность замечать биты, добавленные к сообщению.

Предустановлено на −1

Базовая математика CRC принимает (считает правильно переданными) сообщения, которые при интерпретации как полином кратны полиному CRC. Если к такому сообщению добавляются несколько ведущих нулевых битов, они не изменят его интерпретацию как полинома. Это эквивалентно тому, что 0001 и 1 — одно и то же число.

Но если передаваемое сообщение заботится о ведущих нулевых битах, неспособность базового алгоритма CRC обнаружить такое изменение нежелательна. Если возможно, что ошибка передачи может добавить такие биты, простым решением будет начать с rem регистр сдвига установлен на некоторое ненулевое значение; для удобства обычно используется значение «все единицы». Это математически эквивалентно дополнению (двоичное НЕ) первых n бит сообщения, где n — количество битов в регистре CRC.

Это никак не влияет на генерацию и проверку CRC, если и генератор, и программа проверки используют одно и то же начальное значение. Подойдет любое ненулевое начальное значение, а в некоторых стандартах указаны необычные значения. ^[15] но значение «все единицы» (-1 в двоичном дополнении) является, безусловно, наиболее распространенным. Обратите внимание, что однопроходная генерация/проверка CRC по-прежнему будет давать нулевой результат, если сообщение правильное, независимо от заданного значения.

Пост-инверт

Такая же ошибка может возникнуть в конце сообщения, хотя и с более ограниченным набором сообщений. Добавление 0 битов к сообщению эквивалентно умножению его полинома на x , и если ранее он был кратен полиному CRC, результат этого умножения также будет кратным. Это эквивалентно тому, что, поскольку 726 кратно 11, то и 7260 кратно.

Аналогичное решение можно применить в конце сообщения, инвертируя регистр CRC перед его добавлением к сообщению. Опять же, подойдет любое ненулевое изменение; инвертирование всех битов (исключающее ИЛИ с шаблоном «все единицы») является наиболее распространенным.

Это влияет на однопроходную проверку CRC: вместо нулевого результата, когда сообщение корректно, он выдает фиксированный ненулевой результат. (Если быть точным, результатом является CRC с нулевой предустановкой, но с пост-инвертированием шаблона инверсии.) Как только эта константа получена (например, путем выполнения однопроходной генерации/проверки CRC для произвольного сообщения), его можно использовать непосредственно для проверки правильности любого другого сообщения, проверенного с использованием того же алгоритма CRC.

См. также

Общая категория

Код исправления ошибок
Список хэш-функций
Четность эквивалентна 1-битной CRC с полиномом $x +1$ .

Контрольные суммы без CRC

Ссылки

^ Дуброва, Елена; Мансури, Шоре Шариф (май 2012 г.). «Подход на основе BDD к построению LFSRS для параллельного кодирования CRC» . 42-й международный симпозиум IEEE по многозначной логике , 2012 г. стр. 128–133. дои : 10.1109/ISMVL.2012.20 . ISBN 978-0-7695-4673-5 . S2CID 27306826 .
^ Перейти обратно: ^а ^б Уильямс, Росс Н. (24 сентября 1996 г.). «Безболезненное руководство по алгоритмам обнаружения ошибок CRC V3.00» . Архивировано из оригинала 27 сентября 2006 г. Проверено 16 февраля 2016 г.
^ Сарвате, Дилип В. (август 1998 г.). «Вычисление проверок циклическим избыточным кодом посредством поиска в таблице» . Коммуникации АКМ . 31 (8): 1008–1013. дои : 10.1145/63030.63037 . S2CID 5363350 .
^ «Спецификация портативной сетевой графики (PNG) (второе издание): Приложение D, Пример реализации кода циклической избыточности» . W3C . 10 ноября 2003 г. Проверено 16 февраля 2016 г.
^ «[MS-ABS]: 32-битный алгоритм CRC» . msdn.microsoft.com . Архивировано из оригинала 7 ноября 2017 года . Проверено 4 ноября 2017 г.
^ Кунавис, Мэн; Берри, Флорида (2005). «Систематический подход к созданию высокопроизводительных программных генераторов CRC». 10-й симпозиум IEEE по компьютерам и коммуникациям (ISCC'05) (PDF) . стр. 855–862. дои : 10.1109/ISCC.2005.18 . ISBN 0-7695-2373-0 . S2CID 10308354 .
^ Берри, Фрэнк Л.; Кунавис, Майкл Э. (ноябрь 2008 г.). «Новые алгоритмы поиска по таблицам для высокопроизводительной генерации CRC». Транзакции IEEE на компьютерах . 57 (11): 1550–1560. дои : 10.1109/TC.2008.85 . S2CID 206624854 .
^ Генерация высокооктанового CRC с помощью алгоритма Intel Slicing-by-8 (PDF) (Технический отчет). Интел . Архивировано из оригинала (PDF) 22 июля 2012 г.
^ «Краткое руководство по вычислению CRC» . Архивы ядра Linux .
^ Менон-Сен, Абхиджит (20 января 2017 г.). «Кто изобрел алгоритм нарезки по N CRC32?» .
^ Джон Буллер (15 марта 1996 г.). «Re: 8051 и CRC-CCITT» . Группа новостей : comp.arch.embedded . Usenet: [электронная почта защищена] . Проверено 16 февраля 2016 г.
^ Глез, Рене Ж. (20 января 1997 г.). «Двухэтапное вычисление циклического избыточного кода CRC-32 для сетей ATM» . Журнал исследований и разработок IBM . 41 (6). Армонк, Нью-Йорк : IBM : 705. doi : 10.1147/rd.416.0705 . Архивировано из оригинала 30 января 2009 г. Проверено 16 февраля 2016 г.
^ Дас, Ариндам (2022). «Блочное вычисление циклического избыточного кода с использованием факторизованных матриц Теплица вместо справочной таблицы» . Транзакции IEEE на компьютерах . 72 (4): 1110–1121. дои : 10.1109/TC.2022.3189574 . ISSN 0018-9340 . S2CID 250472783 .
^ Кадач, Эндрю; Дженкинс, Боб (3 сентября 2010 г.). Все, что мы знаем о CRC, но боимся забыть (PDF) (Технический отчет). п. 4. Тот факт, что CRC сообщения, за которым следует его CRC, является постоянной величиной, которая не зависит от сообщения... хорошо известен и уже давно широко используется в телекоммуникационной отрасли. Хороший источник еще большего
^ Например, низкочастотная RFID Техническое описание TMS37157 — Пассивное низкочастотное интерфейсное устройство с EEPROM и интерфейсом транспондера 134,2 кГц (PDF) , Texas Instruments , ноябрь 2009 г., стр. 39 , получено 16 февраля 2016 г. Генератор CRC инициализируется значением 0x3791, как показано на рисунке 50.

Внешние ссылки

ДжонПол Адамовский. «64-битный циклический избыточный код – длинное деление XOR для побайтового поиска в таблице» .

Эндрю Кадарч, Боб Дженкинс. «Эффективная (~ 1 цикл ЦП на байт) реализация CRC» . Гитхаб .

[1] Дуброва, Елена; Мансури, Шоре Шариф (май 2012 г.). «Подход на основе BDD к построению LFSRS для параллельного кодирования CRC» . 42-й международный симпозиум IEEE по многозначной логике , 2012 г. стр. 128–133. дои : 10.1109/ISMVL.2012.20 . ISBN 978-0-7695-4673-5 . S2CID 27306826 .

[williams96-2] Перейти обратно: ^а ^б Уильямс, Росс Н. (24 сентября 1996 г.). «Безболезненное руководство по алгоритмам обнаружения ошибок CRC V3.00» . Архивировано из оригинала 27 сентября 2006 г. Проверено 16 февраля 2016 г.

[3] Сарвате, Дилип В. (август 1998 г.). «Вычисление проверок циклическим избыточным кодом посредством поиска в таблице» . Коммуникации АКМ . 31 (8): 1008–1013. дои : 10.1145/63030.63037 . S2CID 5363350 .

[4] «Спецификация портативной сетевой графики (PNG) (второе издание): Приложение D, Пример реализации кода циклической избыточности» . W3C . 10 ноября 2003 г. Проверено 16 февраля 2016 г.

[5] «[MS-ABS]: 32-битный алгоритм CRC» . msdn.microsoft.com . Архивировано из оригинала 7 ноября 2017 года . Проверено 4 ноября 2017 г.

[6] Кунавис, Мэн; Берри, Флорида (2005). «Систематический подход к созданию высокопроизводительных программных генераторов CRC». 10-й симпозиум IEEE по компьютерам и коммуникациям (ISCC'05) (PDF) . стр. 855–862. дои : 10.1109/ISCC.2005.18 . ISBN 0-7695-2373-0 . S2CID 10308354 .

[7] Берри, Фрэнк Л.; Кунавис, Майкл Э. (ноябрь 2008 г.). «Новые алгоритмы поиска по таблицам для высокопроизводительной генерации CRC». Транзакции IEEE на компьютерах . 57 (11): 1550–1560. дои : 10.1109/TC.2008.85 . S2CID 206624854 .

[8] Генерация высокооктанового CRC с помощью алгоритма Intel Slicing-by-8 (PDF) (Технический отчет). Интел . Архивировано из оригинала (PDF) 22 июля 2012 г.

[9] «Краткое руководство по вычислению CRC» . Архивы ядра Linux .

[10] Менон-Сен, Абхиджит (20 января 2017 г.). «Кто изобрел алгоритм нарезки по N CRC32?» .

[11] Джон Буллер (15 марта 1996 г.). «Re: 8051 и CRC-CCITT» . Группа новостей : comp.arch.embedded . Usenet: [электронная почта защищена] . Проверено 16 февраля 2016 г.

[glaise-12] Глез, Рене Ж. (20 января 1997 г.). «Двухэтапное вычисление циклического избыточного кода CRC-32 для сетей ATM» . Журнал исследований и разработок IBM . 41 (6). Армонк, Нью-Йорк : IBM : 705. doi : 10.1147/rd.416.0705 . Архивировано из оригинала 30 января 2009 г. Проверено 16 февраля 2016 г.

[13] Дас, Ариндам (2022). «Блочное вычисление циклического избыточного кода с использованием факторизованных матриц Теплица вместо справочной таблицы» . Транзакции IEEE на компьютерах . 72 (4): 1110–1121. дои : 10.1109/TC.2022.3189574 . ISSN 0018-9340 . S2CID 250472783 .

[Kadatch2010-14] Кадач, Эндрю; Дженкинс, Боб (3 сентября 2010 г.). Все, что мы знаем о CRC, но боимся забыть (PDF) (Технический отчет). п. 4. Тот факт, что CRC сообщения, за которым следует его CRC, является постоянной величиной, которая не зависит от сообщения... хорошо известен и уже давно широко используется в телекоммуникационной отрасли. Хороший источник еще большего

[15] Например, низкочастотная RFID Техническое описание TMS37157 — Пассивное низкочастотное интерфейсное устройство с EEPROM и интерфейсом транспондера 134,2 кГц (PDF) , Texas Instruments , ноябрь 2009 г., стр. 39 , получено 16 февраля 2016 г. Генератор CRC инициализируется значением 0x3791, как показано на рисунке 50.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]