график Яо

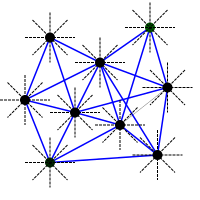
В вычислительной геометрии граф Яо , названный в честь Эндрю Яо , представляет собой своего рода геометрический гаечный ключ , взвешенный неориентированный граф, соединяющий набор геометрических точек со свойством, что для каждой пары точек в графе их кратчайший путь имеет длину это находится в пределах постоянного коэффициента их евклидова расстояния .

Основная идея, лежащая в основе двумерного графа Яо, состоит в том, чтобы окружить каждую из заданных точек равноотстоящими друг от друга лучами , разбив плоскость на сектора с равными углами, и соединить каждую точку с ближайшим соседом в каждом из этих секторов. ^[1] С графом Яо связан целочисленный параметр $k \geq 6$ , который представляет собой количество лучей и секторов, описанных выше; большие значения $k$ дают более близкое приближение к евклидову расстоянию. ^[2] Коэффициент растяжения не более $1/(\cos \theta -\sin \theta )$ , где $\theta$ – угол секторов. ^[3] Ту же идею можно распространить на наборы точек более чем в двух измерениях, но количество требуемых секторов растет экспоненциально с увеличением размера.

Эндрю Яо использовал эти графы для построения многомерных евклидовых минимальных остовных деревьев . ^[3]

Программное обеспечение для рисования графиков Яо

Конусные гаечные ключи в Библиотеке алгоритмов вычислительной геометрии (CGAL)

См. также

Ссылки

^ «Оверлейные сети для беспроводных систем» (PDF) .
^ «Простые топологии» (PDF) .
^ Jump up to: ^а ^б Яо, AC (1982), «О построении минимальных остовных деревьев в k -мерном пространстве и связанных проблемах», SIAM Journal on Computing , 11 (4): 721–736, CiteSeerX 10.1.1.626.3161 , doi : 10.1137/0211059 .

[1] «Оверлейные сети для беспроводных систем» (PDF) .

[2] «Простые топологии» (PDF) .

[YaoPaper-3] Jump up to: ^а ^б Яо, AC (1982), «О построении минимальных остовных деревьев в k -мерном пространстве и связанных проблемах», SIAM Journal on Computing , 11 (4): 721–736, CiteSeerX 10.1.1.626.3161 , doi : 10.1137/0211059 .

[1]

[2]

[3]