Евклидово минимальное остовное дерево

Евклидово минимальное остовное дерево конечного набора точек на евклидовой плоскости более высокой размерности или евклидовом пространстве соединяет точки системой отрезков прямой с точками в качестве конечных точек, минимизируя общую длину сегментов. В нем любые две точки могут достичь друг друга по пути через отрезки прямой. Его можно найти как минимальное остовное дерево с полного графа точками в качестве вершин и евклидовыми расстояниями между точками в качестве весов ребер.

Края минимального остовного дерева встречаются под углами не менее 60 ° и не более шести к вершине. В более высоких измерениях количество ребер на вершину ограничено числом касаний касательных единичных сфер . Общая длина ребер для точек в единичном квадрате не более чем пропорциональна квадратному корню из числа точек. Каждое ребро лежит в пустой области плоскости, и эти области можно использовать для доказательства того, что евклидово минимальное остовное дерево является подграфом других геометрических графов, включая граф относительной окрестности и триангуляцию Делоне . Построив триангуляцию Делоне и затем применив алгоритм минимального остовного дерева графа, минимальное остовное дерево $n$ данные плоские точки могут быть найдены во времени $O(n\log n)$ , как это выражается большой буквой O. Это оптимально в некоторых моделях вычислений, хотя существуют более быстрые рандомизированные алгоритмы для точек с целочисленными координатами. Для точек более высоких размерностей поиск оптимального алгоритма остается открытой проблемой .

Определение и связанные с ним проблемы

Евклидово минимальное остовное дерево для набора $n$ точек на евклидовой плоскости или евклидовом пространстве — это система отрезков прямой , конечными точками которой являются только данные точки, объединение которых включает все точки связного множества и которая имеет минимально возможную общую длину любой такой системы. Такая сеть не может содержать многоугольное кольцо сегментов; если бы он существовал, сеть можно было бы сократить, удалив край многоугольника. Следовательно, сеть минимальной длины образует дерево . Это наблюдение приводит к эквивалентному определению, что евклидово минимальное остовное дерево — это дерево отрезков прямых между парами заданных точек минимальной общей длины. ^[1] То же дерево можно также описать как минимальное остовное дерево взвешенного полного графа , имеющее заданные точки в качестве вершин и расстояния между точками в качестве весов ребер. ^[2] Одни и те же точки могут иметь более одного минимального остовного дерева. Например, для вершин правильного многоугольника удаление любого края многоугольника дает минимальное остовное дерево. ^[3]

В публикациях о евклидовом минимальном остовном дереве его обычно сокращают как «EMST». ^[4]^[5] Их также можно назвать «геометрическими минимальными остовными деревьями». ^[6]^[7] но этот термин можно использовать в более общем смысле для геометрических пространств с неевклидовыми расстояниями, таких как $L п$ пространства . ^[8] Когда контекст евклидовых наборов точек ясен, их можно назвать просто «минимальными остовными деревьями». ^[9]^[10]^[11]

Несколько других стандартных геометрических сетей тесно связаны с евклидовым минимальным остовным деревом:

снова Задача о дереве Штейнера ищет систему отрезков прямых, соединяющих все заданные точки, но без требования, чтобы отрезки начинались и заканчивались только в заданных точках. В этой задаче дополнительные точки могут быть добавлены в качестве конечных точек сегмента, что позволяет дереву Штейнера быть короче минимального остовного дерева. ^[12]
В евклидовой задаче о пути коммивояжера соединительные отрезки линий должны начинаться и заканчиваться в заданных точках, как в остовном дереве и в отличие от дерева Штейнера; кроме того, каждая точка может касаться не более двух отрезков прямой, поэтому результат образует полигональную цепочку . Из-за этого ограничения оптимальный путь может быть длиннее минимального евклидова остовного дерева, но не более чем в два раза. ^[2]
Геометрические ключи — это сети с малым весом, которые, как и минимальное связующее дерево, соединяют все точки. В отличие от минимального остовного дерева, все эти соединительные пути должны быть короткими и иметь длину, пропорциональную расстоянию между точками, которые они соединяют. Для достижения этого свойства эти сети обычно имеют циклы и поэтому не являются деревьями. ^[13]

Характеристики

Углы и степени вершин

Двенадцать единичных сфер касаются центральной единичной сферы. Минимальное остовное дерево из 13 центральных точек имеет степень 12 в центральной точке.

Всякий раз, когда два ребра евклидова минимального остовного дерева встречаются в вершине, они должны образовывать угол 60 ° или более, причем равенство возникает только тогда, когда они образуют две стороны равностороннего треугольника . Это связано с тем, что для двух ребер, образующих любой более острый угол, одно из двух ребер может быть заменено третьим, более коротким ребром треугольника, который они образуют, образуя дерево с меньшей общей длиной. ^[14] Для сравнения, проблема дерева Штейнера имеет более сильную границу угла: оптимальное дерево Штейнера имеет все углы не менее 120 °. ^[12]

Та же граница угла в 60 ° также встречается в задаче о числе поцелуев , когда нужно найти максимальное количество единичных сфер в евклидовом пространстве, которые могут касаться центральной единичной сферы без пересечения каких-либо двух сфер (за пределами точки касания). Центральные точки этих сфер имеют минимальное остовное дерево в форме звезды , при этом центральная точка примыкает ко всем остальным точкам. Обратно, для любой вершины $v$ любого минимального остовного дерева можно построить непересекающиеся единичные сферы с центром в $v$ а в точках по две единицы вдоль каждого из его ребер с касанием для каждого соседа $v$ . Поэтому в $n$ В -мерном пространстве максимально возможная степень вершины (количество связанных с ней ребер остовного дерева) равна числу целующихся сфер в $n$ размеры. ^[15] Плоские минимальные остовные деревья имеют степень не более шести, а когда дерево имеет степень шесть, всегда существует другое минимальное остовное дерево с максимальной степенью пять. ^[7] Трехмерные минимальные остовные деревья имеют степень не более двенадцати. ^[15] Единственными высшими измерениями, в которых известно точное значение числа поцелуев, являются четыре, восемь и 24 измерения. ^[16]

Для точек, сгенерированных случайным образом из данного непрерывного распределения, минимальное остовное дерево почти наверняка уникально. Число вершин любой заданной степени сходится для большого числа вершин к постоянному числу вершин, умноженному на это число. Значения этих констант зависят от степени и распределения. Однако даже для простых случаев, таких как количество листьев для точек, равномерно распределенных в единичном квадрате, их точные значения неизвестны. ^[17]

Пустые регионы

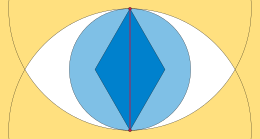
Для любого края $uv$ любого евклидова минимального остовного дерева, линза (или vesica piscis ), образованная пересечением двух окружностей с $uv$ поскольку их радиусы не могут иметь никакой другой заданной вершины $w$ в его интерьере. Другими словами, если у какого-либо дерева есть край $uv$ линза которого содержит третью точку $w$ , то оно не минимальной длины. Ибо, согласно геометрии двух кругов, $w$ было бы ближе к обоим $u$ и $v$ чем они друг другу. Если край $uv$ были сняты с дерева, $w$ останется подключенным к одному из $u$ и $v$ , но не другой. Замена снятой кромки $uv$ к $uw$ или $vw$ (какое из этих двух ребер снова соединяет $w$ до вершины, от которой оно было отключено) создаст более короткое дерево. ^[12]

Для любого края $uv$ любого евклидова минимального остовного дерева ромб с углами 60° и 120°, имеющий $uv$ как и его длинная диагональ, не пересекается с ромбами, образованными аналогично всеми остальными ребрами. Два ребра, имеющие общую конечную точку, не могут иметь перекрывающихся ромбов, поскольку это будет означать, что угол кромки будет острее 60 °, а два непересекающихся ребра не могут иметь перекрывающихся ромбов; если бы они это сделали, то более длинное из двух ребер можно было бы заменить более коротким ребром среди тех же четырех вершин. ^[12]

Суперграфы

Некоторые геометрические графы имеют определения, включающие пустые области в множествах точек, из чего следует, что они содержат каждое ребро, которое может быть частью евклидова минимального остовного дерева. К ним относятся:

Граф относительной окрестности , который имеет ребро между любой парой точек всякий раз, когда определяемая ими линза пуста.
Граф Габриэля , который имеет ребро между любой парой точек всякий раз, когда круг, диаметр которого составляет пару, пуст.
Триангуляция Делоне , которая имеет ребро между любой парой точек всякий раз, когда существует пустой круг, имеющий пару в качестве хорды.
Граф Уркарта , образованный из триангуляции Делоне путем удаления самого длинного ребра каждого треугольника. Для каждого оставшегося ребра вершины треугольников Делоне, использующие это ребро, не могут лежать в пределах пустой лунки графа относительной окрестности.

Поскольку критерии пустой области для этих графов становятся все более слабыми, эти графы образуют упорядоченную последовательность подграфов. То есть, используя «⊆» для обозначения отношений подмножеств между их ребрами, эти графы имеют отношения:

Евклидово минимальное остовное дерево ⊆ граф относительной окрестности ⊆ граф Уркарта ⊆ граф Габриэля ⊆ триангуляция Делоне. ^[18]^[19]

Другой граф, который гарантированно содержит минимальное остовное дерево, — это граф Яо , определяемый для точек плоскости путем разделения плоскости вокруг каждой точки на шесть секторов по 60° и соединения каждой точки с ближайшим соседом в каждом сегменте. Полученный граф содержит граф относительной окрестности, поскольку две вершины с пустой линзой должны быть ближайшими соседями друг к другу в своих клиньях. Как и в случае со многими другими геометрическими графами, приведенными выше, это определение можно обобщить на более высокие размерности, и (в отличие от триангуляции Делоне) его обобщения всегда включают линейное количество ребер. ^[20]^[21]

Общая длина

Для $n$ точек в единичном квадрате (или любой другой фиксированной форме), общая длина минимальных ребер остовного дерева равна $O({\sqrt {n}})$ . Некоторые наборы точек, например точки, равномерно расположенные в ${\sqrt {n}}\times {\sqrt {n}}$ сетке, достигните этой границы. ^[12] Для точек единичного гиперкуба в $d$ -мерного пространства, соответствующая оценка равна $O(n^{(d-1)/d})$ . ^[22] Та же самая граница применима к ожидаемой общей длине минимального остовного дерева для $n$ точки выбираются равномерно и независимо от единичного квадрата или единичного гиперкуба. ^[23] Возвращаясь к единичному квадрату, сумма квадратов длин ребер минимального остовного дерева равна $O(1)$ . Эта оценка следует из наблюдения, что ребра имеют непересекающиеся ромбы, площадь которых пропорциональна квадрату длин ребер. $O({\sqrt {n}})$ Ограничение на общую длину следует из неравенства Коши – Шварца . ^[12]

Другая интерпретация этих результатов состоит в том, что средняя длина ребра для любого набора точек единичного квадрата равна $O(1/{\sqrt {n}})$ , не более чем пропорционально шагу точек регулярной сетки; и что для случайных точек единичного квадрата средняя длина пропорциональна $1/{\sqrt {n}}$ . Однако в случайном случае с большой вероятностью самое длинное ребро имеет длину примерно ${\sqrt {\frac {\log n}{\pi n}}},$ дольше, чем в среднем, в непостоянный коэффициент. С высокой вероятностью самое длинное ребро образует лист остовного дерева и соединяет точку, далекую от всех остальных точек, с ее ближайшим соседом. Для большого количества точек распределение длины самого длинного ребра вокруг его ожидаемого значения сходится к распределению Гамбеля . ^[24]

Любой геометрический гаечный ключ , подграф полного геометрического графа, кратчайшие пути которого приближаются к евклидову расстоянию, должен иметь общую длину ребра, по крайней мере, такую же большую, как минимальное остовное дерево, и одной из стандартных мер качества геометрического гаечного ключа является соотношение между его общая длина и минимальное остовное дерево для тех же точек. Некоторые методы построения гаечных ключей, такие как жадный геометрический гаечный ключ , позволяют добиться постоянной границы этого отношения. ^[13] Было высказано предположение, что коэффициент Штейнера , максимально возможное соотношение между общей длиной минимального остовного дерева и дерева Штейнера для одного и того же набора точек на плоскости, равен $2/{\sqrt {3}}\approx 1.1547$ , отношение трёх точек в равностороннем треугольнике . ^[12]

Подразделение

Если каждое ребро евклидова минимального остовного дерева подразделяется путем добавления новой точки в его средней точке, то полученное дерево по-прежнему остается минимальным остовным деревом расширенного набора точек. Повторение этого процесса подразделения позволяет разделить евклидово минимальное остовное дерево сколь угодно точно. Однако разделение только некоторых ребер или разделение ребер в точках, отличных от средней точки, может привести к созданию набора точек, для которого разделенное дерево не является минимальным остовным деревом. ^[25]

Вычислительная сложность

Для точек любого измерения минимальное остовное дерево может быть построено за время. $O(n^{2})$ путем построения полного графа с ребром между каждой парой точек, взвешенного по евклидову расстоянию , а затем применения к нему алгоритма минимального остовного дерева графа, такого как алгоритм Прима – Дейкстры – Ярника или алгоритм Борувки . Эти алгоритмы могут занять время $O(n^{2})$ на полных графах, в отличие от другого распространенного варианта, алгоритма Краскала , который медленнее, поскольку включает в себя сортировку всех расстояний. ^[13] Для точек в маломерных пространствах проблема может быть решена быстрее, как подробно описано ниже.

Вычисление евклидовых расстояний включает в себя вычисление квадратного корня . При любом сравнении весов ребер сравнение квадратов евклидовых расстояний, а не самих расстояний, дает тот же порядок и поэтому не меняет остальную часть вычислений дерева. Этот ярлык ускоряет расчет и позволяет построить минимальное связующее дерево для точек с целочисленными координатами, используя только целочисленную арифметику. ^[20]

Два измерения

Более быстрый подход к поиску минимального остовного дерева плоских точек использует то свойство, что оно является подграфом триангуляции Делоне:

Вычислите триангуляцию Делоне, что можно сделать в $O(n\log n)$ время. Поскольку триангуляция Делоне представляет собой плоский граф , она имеет не более $3n-6$ края.
Пометьте каждое ребро его (квадратной) длиной.
Запустите алгоритм минимального связующего дерева графа. Поскольку существуют $O(n)$ края, для этого требуется $O(n\log n)$ время с использованием любого из стандартных алгоритмов минимального связующего дерева.

В результате получается алгоритм, принимающий $O(n\log n)$ время, ^[2] оптимален в определенных моделях вычислений (см. ниже ).

Если входные координаты являются целыми числами и могут использоваться в качестве индексов массива , возможны более быстрые алгоритмы: триангуляция Делоне может быть построена с помощью рандомизированного алгоритма в $O(n\log \log n)$ ожидаемое время. ^[26] Кроме того, поскольку триангуляция Делоне представляет собой плоский граф , его минимальное остовное дерево может быть найдено за линейное время с помощью варианта алгоритма Борувки, который удаляет все ребра, кроме самого дешевого, между каждой парой компонентов после каждого этапа алгоритма. ^[13]^[27] Следовательно, общее ожидаемое время для этого алгоритма равно $O(n\log \log n)$ . ^[26] В другом направлении триангуляция Делоне может быть построена из минимального остовного дерева в почти линейном временном интервале. $O(n\log ^{*}n)$ , где $\log ^{*}$ обозначает повторный логарифм . ^[28]

Высшие измерения

Проблему также можно обобщить на $n$ точки в $d$ -мерное пространство $\mathbb {R} ^{d}$ . В более высоких измерениях связность определяется триангуляцией Делоне (которая также разделяет выпуклую оболочку на $d$ -мерные симплексы ) содержит минимальное остовное дерево; однако триангуляция может содержать полный граф. ^[4] Следовательно, для нахождения евклидова минимального остовного дерева как остовного дерева полного графа или как остовного дерева триангуляции Делоне требуется как $O(dn^{2})$ время. Для трех измерений минимальное остовное дерево можно найти за время. $O{\bigl (}(n\log n)^{4/3}{\bigr )}$ , и в любом большем измерении, во времени $O\left(n^{2-{\frac {2}{\lceil d/2\rceil +1}}+\varepsilon }\right)$ для любого $\varepsilon >0$ — быстрее, чем квадратичное время для алгоритмов полного графа и триангуляции Делоне. ^[4]

Оптимальная временная сложность для минимальных остовных деревьев более высокой размерности остается неизвестной. ^[29] но тесно связано со сложностью вычисления ближайших бихроматических пар . В задаче о бихроматической ближайшей паре входными данными является набор точек двух разных цветов (скажем, красного и синего). На выходе получается пара красной точки и синей точки с минимально возможным расстоянием. Эта пара всегда образует одно из ребер минимального остовного дерева. Следовательно, задача о бихроматической ближайшей паре может быть решена за время, необходимое для построения минимального остовного дерева и сканирования его ребер в поисках кратчайшего красно-синего ребра. И наоборот, для любой красно-синей раскраски любого подмножества данного набора точек бихроматическая ближайшая пара дает одно ребро минимального остовного дерева подмножества. Тщательно выбирая последовательность раскрасок подмножеств и находя ближайшую бихроматическую пару каждой подзадачи, минимальное остовное дерево можно найти за время, пропорциональное оптимальному времени для поиска ближайших бихроматических пар для того же числа точек, каким бы ни было это оптимальное время. оказывается. ^[4]^[11]

Для равномерно случайных наборов точек в любом ограниченном измерении граф Яо ^[20] или триангуляция Делоне имеют линейное ожидаемое количество ребер, гарантированно содержат минимальное остовное дерево и могут быть построены за линейное ожидаемое время. ^[21]^[6]^[30] Из этих графов само минимальное остовное дерево может быть построено за линейное время с использованием рандомизированного алгоритма линейного времени для минимальных остовных деревьев графа . ^[31] Однако низкая производительность этих методов на входных данных, поступающих из кластерных данных, побудила исследователей в области разработки алгоритмов разработать методы с несколько более медленной скоростью. $O(n\log n)$ с привязкой по времени для случайных входных данных или входных данных, расстояния и кластеризация которых напоминают расстояния и кластеризацию случайных данных, при этом демонстрируя лучшую производительность на реальных данных. ^[8]^[32]^[5]

Хорошо разделенное парное разложение — это семейство пар подмножеств данных точек, при котором каждая пара точек принадлежит одной из этих пар подмножеств и все пары точек, происходящие из одной и той же пары подмножеств, имеют примерно такой же длины. Можно найти хорошо разделенное парное разложение с линейным числом подмножеств и репрезентативной парой точек для каждого подмножества во времени. $O(n\log n)$ . Минимальное остовное дерево графа, образованное этими репрезентативными парами, является тогда приближением к минимальному остовному дереву. Используя эти идеи, А. $(1+\varepsilon )$ -приближение к минимальному остовному дереву можно найти в $O(n\log n)$ время, для постоянного $\varepsilon$ . Точнее, выбирая каждую репрезентативную пару для аппроксимации ближайшей пары в своем классе эквивалентности и тщательно варьируя качество этой аппроксимации для разных пар, зависимость от $\varepsilon$ в ограниченном времени может быть задано как $O(n\log n+(\varepsilon ^{-2}\log ^{2}{\tfrac {1}{\varepsilon }})n),$ для любого фиксированного размера. ^[33]

Динамический и кинетический

Евклидово минимальное остовное дерево было по-разному обобщено на системы перемещения или изменения точек:

Если набор точек подвергается последовательности динамических вставок или удалений точек, каждое из этих обновлений вызывает ограниченное количество изменений в минимальном остовном дереве точек. Когда последовательность обновления для точек на плоскости известна заранее, изменение после каждой вставки или удаления можно найти во времени. $O(\log ^{2}n)$ за вставку или удаление. ^[34] Когда обновления должны обрабатываться онлайн , более медленный (но все же полилогарифмический) $O(\log ^{10}n)$ сроки известны. ^[35] Для многомерных версий задачи время обновления меньше, но все равно сублинейное. ^[36]
Для $n$ точек, движущихся линейно с постоянной скоростью, или с помощью более общих алгебраических движений, минимальное остовное дерево будет меняться последовательностью перестановок, при которых одно ребро удаляется, а другое заменяет его в момент времени, когда оба имеют одинаковую длину. ^[37] Для линейных движений число изменений не более чем несколько больше, чем $n^{25/9}$ . ^[38] Для более общих алгебраических движений существует почти кубическая верхняя граница количества перестановок, основанная на теории последовательностей Давенпорта – Шинцеля . ^[39]
Задача о минимальном движущемся остовном дереве снова касается точек, движущихся линейно с постоянной скоростью в течение интервала времени, и ищет одно дерево, которое минимизирует максимальную сумму весов, возникающих в любой момент в течение этого интервала. Точно вычислить NP-трудно, но можно аппроксимировать с точностью до двух раз за полиномиальное время. ^[40]
Кинетическая задача евклидова минимального остовного дерева требует кинетической структуры данных , которая могла бы поддерживать минимальное остовное дерево, поскольку его точки подвергаются как непрерывным движениям, так и вставкам и удалениям. В нескольких статьях изучались такие структуры, ^[41]^[42]^[43]^[44]^[45] и известна кинетическая структура для алгебраически движущихся точек с почти кубическим общим временем, почти соответствующим ограничению количества перестановок. ^[44]

Нижняя граница

Асимптотическая нижняя граница $\Omega (n\log n)$ Задача евклидового минимального остовного дерева может быть установлена в ограниченных моделях вычислений. К ним относятся модели алгебраического дерева решений и дерева алгебраических вычислений , в которых алгоритм имеет доступ к входным точкам только через определенные ограниченные примитивы, которые выполняют простые алгебраические вычисления над своими координатами. В этих моделях задача о ближайшей паре точек требует $\Omega (n\log n)$ время, но ближайшая пара обязательно является ребром минимального остовного дерева, поэтому минимальное остовное дерево также требует столько же времени. Поэтому алгоритмы построения планарного минимального остовного дерева за время $O(n\log n)$ в рамках этой модели, например, с использованием триангуляции Делоне, являются оптимальными. ^[46] Однако эти нижние границы не применяются к моделям вычислений с целочисленными координатами точки, в которых побитовые операции и операции индексации таблиц разрешены с этими координатами. В этих моделях возможны более быстрые алгоритмы, как описано выше. ^[26]

Приложения

Очевидным применением евклидовых минимальных связующих деревьев является поиск самой дешевой сети проводов или труб для соединения множества мест, предполагая, что ссылки стоят фиксированную сумму за единицу длины. Первые публикации о минимальных связующих деревьях в более общем плане касались географической версии проблемы, включая проектирование электрической сети для южной Моравии . ^[47] а применение для минимизации длины проводов в цепях было описано в 1957 году Лоберманом и Вайнбергером. ^[48]

Минимальные связующие деревья тесно связаны с кластеризацией с одной связью , одним из нескольких методов иерархической кластеризации . Ребра минимального остовного дерева, отсортированные по их длине, задают порядок объединения кластеров в более крупные кластеры в этом методе кластеризации. Как только эти ребра будут найдены с помощью любого алгоритма, их можно использовать для построения односвязной кластеризации во времени. $O(n\log n)$ . ^[1] Хотя длинные тонкие формы кластеров, полученные с помощью кластеризации с одной связью, могут плохо подходить для определенных типов данных, таких как смеси гауссовых распределений , они могут быть хорошим выбором в приложениях, где ожидается, что сами кластеры будут иметь длинные тонкие формы. например, при моделировании темной материи галактик гало . ^[5] В географической информатике несколько исследовательских групп использовали минимальные остовные деревья центроидов зданий для идентификации значимых кластеров зданий, например, путем удаления ребер, определенных каким-либо другим способом как несовместимые. ^[49]

Минимальные остовные деревья также использовались для определения формы кривых на плоскости по точкам, выбранным вдоль кривой. Для гладкой кривой, выбранной более точно, чем размер ее локального объекта , минимальное остовное дерево будет формировать путь, соединяющий последовательные точки вдоль кривой. В более общем смысле, подобные методы могут распознавать кривые, нарисованные пунктиром или пунктиром, а не как единый связный набор. Приложения этого метода поиска кривых включают физику элементарных частиц для автоматического определения следов, оставленных частицами в пузырьковой камере . ^[50] Более сложные версии этой идеи позволяют находить кривые из облака зашумленных точек выборки, которые примерно следуют контуру кривой, используя топологию остовного дерева в качестве руководства для метода скользящих наименьших квадратов . ^[51]

Другое применение минимальных остовных деревьев — алгоритм аппроксимации с постоянным коэффициентом для евклидовой задачи коммивояжера , задачи поиска кратчайшей полигонализации множества точек. Обход границы минимального остовного дерева может приблизить оптимальный тур коммивояжера с точностью до двух раз от оптимальной длины. ^[2] Однако более точные схемы аппроксимации за полиномиальное время . для этой задачи известны ^[52] В беспроводных одноранговых сетях широковещательная рассылка сообщений по путям минимального связующего дерева может быть точным приближением к широковещательной маршрутизации с минимальной энергией, которую, опять же, трудно точно вычислить. ^[53]^[54]^[55]^[56]

Реализация

Задача реализации евклидовых минимальных остовных деревьев принимает абстрактное дерево в качестве входных данных и ищет геометрическое местоположение для каждой вершины дерева (в пространстве некоторого фиксированного измерения), чтобы данное дерево равнялось минимальному остовному дереву этих точек. Не каждое абстрактное дерево имеет такую реализацию; например, дерево должно подчиняться числу поцелуев, привязанному к степени каждой вершины. Существуют дополнительные ограничения; например, плоское минимальное остовное дерево не может иметь вершину шестой степени, смежную с вершиной пятой или шестой степени. ^[7] Определить, существует ли двумерная реализация, NP-трудно . Однако доказательство сложности зависит от того факта, что вершины шестой степени в дереве имеют очень ограниченный набор реализаций: соседи такой вершины должны быть помещены в вершины правильного шестиугольника с центром в этой вершине. ^[57] Действительно, для деревьев максимальной пятой степени всегда существует плоская реализация. ^[7] Аналогично, для деревьев максимальной степени десять всегда существует трехмерная реализация. ^[10] Для этих реализаций некоторым деревьям могут потребоваться ребра экспоненциальной длины и ограничивающие прямоугольники экспоненциальной площади относительно длины их самого короткого ребра. ^[58] Деревья максимальной степени четыре имеют меньшие плоские реализации с полиномиально ограниченными длинами ребер и ограничивающими рамками. ^[9]

См. также

Прямолинейное минимальное остовное дерево , минимальное остовное дерево с расстояниями, измеренными с использованием геометрии такси.

Ссылки

^ Jump up to: Перейти обратно: ^а ^б Гауэр, Дж. К.; Росс, GJS (1969), «Минимальные остовные деревья и кластерный анализ с одной связью», Applied Статистика , 18 (1): 54–61, doi : 10.2307/2346439 , JSTOR 2346439 , MR 0242315
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Шамос, Майкл Ян ; Хоуи, Дэн (1975), «Задачи ближайшей точки», 16-й ежегодный симпозиум по основам информатики, Беркли, Калифорния, США, 13–15 октября 1975 г. , Компьютерное общество IEEE, стр. 151–162, doi : 10.1109/ SFCS.1975.8 , MR 0426498 , S2CID 40615455
^ Бозе, Просенджит ; Деврой, Люк ; Эванс, Уильям; Киркпатрик, Дэвид (2006), «Об отношении охвата графов Габриэля и β-скелетов», SIAM Journal on Discrete Mathematics , 20 (2): 412–427, doi : 10.1137/S0895480197318088 , MR 2257270
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Агарвал, ПК ; Эдельсбруннер, Х. ; Шварцкопф, О .; Вельцль, Э. (1991), «Евклидовы минимальные остовные деревья и бихроматические ближайшие пары», Discrete & Computational Geometry , 6 (1), Springer: 407–422, doi : 10.1007/BF02574698 , MR 1115099
^ Jump up to: Перейти обратно: ^а ^б ^с Марч, Уильям Б.; Рам, Парикшит; Грей, Александр Г. (2010), «Быстрое евклидово минимальное остовное дерево: алгоритм, анализ и приложения», Рао, Бхарат; Кришнапурам, Баладжи; Томкинс, Эндрю; Ян, Цян (ред.), Труды 16-й Международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных, Вашингтон, округ Колумбия, США, 25–28 июля 2010 г. , стр. 603–612, doi : 10.1145/1835804.1835882 , S2CID 186025
^ Jump up to: Перейти обратно: ^а ^б Кларксон, Кеннет Л. (1989), «Алгоритм для геометрических минимальных остовных деревьев, требующий почти линейного ожидаемого времени», Algorithmica , 4 (1–4): 461–469, doi : 10.1007/BF01553902 , MR 1019387 , S2CID 22176641
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Монма, Клайд; Сури, Субхаш (1992), «Переходы в геометрических минимальных остовных деревьях», Дискретная и вычислительная геометрия , 8 (3): 265–293, doi : 10.1007/BF02293049 , MR 1174358 , S2CID 30101649
^ Jump up to: Перейти обратно: ^а ^б Нарасимхан, Гири; Захариасен, Мартин; Чжу, Цзяньлинь (2000), «Эксперименты с вычислением геометрических минимальных остовных деревьев», Материалы 2-го семинара по разработке алгоритмов и экспериментам , стр. 183–196.
^ Jump up to: Перейти обратно: ^а ^б Фрати, Фабрицио; Кауфманн, Майкл (2011), «Границы полиномиальной области для вложений деревьев MST», Вычислительная геометрия: теория и приложения , 44 (9): 529–543, doi : 10.1016/j.comgeo.2011.05.005 , MR 2819643 , S2CID 5634139
^ Jump up to: Перейти обратно: ^а ^б Кинг, Джеймс А. (2006), «Реализация минимальных остовных деревьев степени 10 в трехмерном пространстве» (PDF) , Материалы 18-й ежегодной канадской конференции по вычислительной геометрии, CCCG 2006, 14–16 августа 2006 г., Королевский университет, Онтарио, Канада , стр. 39–42.
^ Jump up to: Перейти обратно: ^а ^б Крзнарич, Драго; Левкопулос, Христос; Нильссон, Бенгт Дж. (1999), "Минимум пролетных деревьев в $d$ Dimensions», Nordic Journal of Computing , 6 (4): 446–461, MR 1736451. Эта версия этой статьи недоступна в Интернете; вместо этого см. версию той же статьи, опубликованную на конференции 1997 года, дои : 10.1007/3-540-63397-9_26 .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Гилберт, EN ; Поллак, Х.О. (1968), «Минимальные деревья Штейнера», SIAM Journal on Applied Mathematics , 16 (1): 1–29, doi : 10.1137/0116001 , JSTOR 2099400 , MR 0223269
^ Jump up to: Перейти обратно: ^а ^б ^с ^д Эппштейн, Дэвид (1999), «Соединительные деревья и гаечные ключи» (PDF) , в Саке, Ж.-Р. ; Уррутиа, Дж. (ред.), Справочник по вычислительной геометрии , Elsevier, стр. 425–461, MR 1746681.
^ Георгакопулос, Джордж; Пападимитриу, Христос Х. (1987), «Проблема дерева 1 Штейнера», Журнал алгоритмов , 8 (1): 122–130, doi : 10.1016/0196-6774(87)90032-0 , MR 0875330
^ Jump up to: Перейти обратно: ^а ^б Робинс, Г.; Салове, Дж. С. (1995), «Минимальные остовные деревья низкой степени», Дискретная и вычислительная геометрия , 14 (2): 151–165, doi : 10.1007/BF02570700 , MR 1331924 , S2CID 16040977
^ Пфендер, Флориан; Циглер, Гюнтер М. (сентябрь 2004 г.), «Целующиеся числа, упаковки сфер и некоторые неожиданные доказательства» (PDF) , Уведомления Американского математического общества : 873–883
^ Стил, Дж. Майкл ; Шепп, Лоуренс А.; Эдди, Уильям Ф. (1987), «О количестве листьев евклидова минимального остовного дерева», Journal of Applied Probability , 24 (4): 809–826, doi : 10.2307/3214207 , JSTOR 3214207 , MR 0913823 , S2CID 29026025
^ Препарата, Франко П .; Шамос, Майкл Ян (1985), Вычислительная геометрия: Введение , Тексты и монографии по информатике, Springer-Verlag, Нью-Йорк, стр. 263, номер домена : 10.1007/978-1-4612-1098-6 , ISBN. 0-387-96131-3 , МР 0805539 , S2CID 206656565
^ Туссен, GT (1980), «Комментарий: Алгоритмы вычисления графа относительной окрестности», Electronics Letters , 16 (22): 860, Bibcode : 1980ElL....16..860T , doi : 10.1049/el:19800611 ; ответ Уркарта, стр. 860–861.
^ Jump up to: Перейти обратно: ^а ^б ^с Яо, Эндрю Чи Чи (1982), «О построении минимальных остовных деревьев в $k$ -мерных пространствах и связанных проблемах», SIAM Journal on Computing , 11 (4): 721–736, doi : 10.1137/0211059 , MR 0677663
^ Jump up to: Перейти обратно: ^а ^б Бентли, Джон Луис ; Вейде, Брюс В.; Яо, Эндрю К. (1980), «Алгоритмы оптимального ожидаемого времени для задач ближайшей точки» , Транзакции ACM в математическом программном обеспечении , 6 (4): 563–580, doi : 10.1145/355921.355927 , MR 0599977 , S2CID 17238717
^ Стил, Дж. Майкл ; Снайдер, Тимоти Лоу (1989), «Темпы роста в наихудшем случае некоторых классических задач комбинаторной оптимизации» , SIAM Journal on Computing , 18 (2): 278–287, doi : 10.1137/0218019 , MR 0986667
^ Стил, Дж. Майкл (1988), «Темпы роста евклидовых минимальных остовных деревьев со взвешенными по мощности ребрами», Annals of Probability , 16 (4): 1767–1787, doi : 10.1214/aop/1176991596 , JSTOR 2243991 , MR 0958215
^ Пенроуз, Мэтью Д. (1997), «Самое длинное ребро случайного минимального остовного дерева», Анналы прикладной вероятности , 7 (2): 340–361, doi : 10.1214/aoap/1034625335 , MR 1442317
^ Бойс, WM; Гэри, MR ; Джонсон, Д.С. (1978), «Заметка о разбиении минимальных остовных деревьев пополам», Networks , 8 (3): 187–192, doi : 10.1002/net.3230080302 , MR 0491324
^ Jump up to: Перейти обратно: ^а ^б ^с Бучин, Кевин; Мульцер, Вольфганг (2011), «Триангуляции Делоне за $время O$ (сортировка ( $n$ )) и более», Журнал ACM , 58 (2): A6:1–A6:27, doi : 10.1145/1944345.1944347 , MR 2786587 , S2CID 11316974
^ Мареш, Мартин (2004), «Два алгоритма с линейным временем для MST на второстепенных классах замкнутых графов» (PDF) , Archivum Mathematicum , 40 (3): 315–320, MR 2107027
^ Девиллерс, Оливье (1992), «Рандомизация дает простой $O (n log * n)$ алгоритмы для сложных $Ω(n)$ задач » (PDF) , Международный журнал вычислительной геометрии и приложений , 2 (1): 97–111, doi : 10.1142/S021819599200007X , MR 1159844 , S2CID 60203
^ О'Рурк, Дж .; Демейн, Э. (2001–2002), «Проблема 5: Евклидово минимальное остовное дерево» , Проект открытых проблем , Колледж Смита
^ Дуайер, Рекс А. (1991), «Многомерные диаграммы Вороного в линейном ожидаемом времени», Discrete & Computational Geometry , 6 (4): 343–367, doi : 10.1007/BF02574694 , MR 1098813
^ Каргер, Дэвид Р .; Кляйн, Филип Н.; Тарьян, Роберт Э. (1995), «Рандомизированный алгоритм линейного времени для поиска минимальных остовных деревьев», Journal of the ACM , 42 (2): 321–328, doi : 10.1145/201019.201022 , MR 1409738 , S2CID 832583
^ Чаттерджи, С.; Коннор, М.; Кумар, П. (2010), «Геометрические минимальные охватывающие деревья с GeoFilterKruskal», в Фесте, Паола (ред.), Экспериментальные алгоритмы: 9-й Международный симпозиум, SEA 2010, остров Искья, Неаполь, Италия, 20-22 мая 2010 г., Труды , Конспекты лекций по информатике, вып. 6049, Springer-Verlag, стр. 486–500, номер документа : 10.1007/978-3-642-13193-6_41 , ISBN. 978-3-642-13192-9
^ Арья, Сунил; Маунт, Дэвид М. (2016), «Быстрый и простой алгоритм вычисления приближенных евклидовых минимальных остовных деревьев», Краутгеймер, Роберт (редактор), Труды двадцать седьмого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам, SODA 2016 , Арлингтон, Вирджиния, США, 10–12 января 2016 г. , стр. 1220–1233, doi : 10.1137/1.9781611974331.ch85 , MR 3478461
^ Эппштейн, Дэвид (1994), «Автономные алгоритмы для динамических задач минимального остовного дерева» , Journal of Algorithms , 17 (2): 237–250, doi : 10.1006/jagm.1994.1033 , MR 1291541
^ Чан, Тимоти М. (2010), «Динамическая структура данных для трехмерных выпуклых оболочек и двумерных запросов к ближайшему соседу», Журнал ACM , 57 (3): Статья 16, doi : 10.1145/1706591.1706596 , MR 2665885 , S2CID 47454142
^ Эппштейн, Дэвид (1995), «Динамические евклидовы минимальные остовные деревья и экстремумы бинарных функций», Discrete & Computational Geometry , 13 (1): 111–122, doi : 10.1007/BF02574030 , MR 1300511 , S2CID 7339165
^ Като, Н.; Токуяма, Т.; Ивано, К. (1995), «О минимальном и максимальном остовном дереве линейно движущихся точек», Discrete & Computational Geometry , 13 (2): 161–176, doi : 10.1007/BF02574035 , MR 1314960
^ Чан, Тимоти М. (2003), «Об уровнях в расположении кривых», Discrete & Computational Geometry , 29 (3): 375–393, doi : 10.1007/s00454-002-2840-2 , MR 1961005 , S2CID 18966889
^ Рахмати, Захед; Зарей, Алиреза (2010), «Комбинаторные изменения евклидова минимального остова дерева движущихся точек на плоскости» (PDF) , Материалы 22-й ежегодной канадской конференции по вычислительной геометрии, Виннипег, Манитоба, Канада, 9–11 августа 2010 г. , стр. 43–45
^ Акитая, Хьюго А.; Биниаз, Ахмад; Бозе, Просенджит ; Де Каруфель, Жан-Лу; Махешвари, Анил; да Силвейра, Луис Фернандо Шульц Ксавьер; Смид, Михил (2021), «Задача о минимальном движущемся остовном дереве», Любив, Анна ; Салаватипур, Мохаммад Р. (ред.), Алгоритмы и структуры данных: 17-й Международный симпозиум, WADS 2021, виртуальное мероприятие, 9–11 августа 2021 г., Материалы , конспекты лекций по информатике, том. 12808, Springer, стр. 15–28, doi : 10.1007/978-3-030-83508-8_2 , ISBN. 978-3-030-83507-1 , S2CID 234599877
^ Баш, Жюльен; Гибас, Леонидас Дж .; Чжан, Ли (1997), «Проблемы близости движущихся точек», в Буассонна, Жан-Даниэль (ред.), Труды тринадцатого ежегодного симпозиума по вычислительной геометрии, Ницца, Франция, 4–6 июня 1997 г. , Ассоциация вычислительной техники. Machinery, стр. 344–351, doi : 10.1145/262839.262998 , S2CID 15556637.
^ Агарвал, Панкадж К .; Эппштейн, Дэвид ; Гибас, Леонидас Дж .; Хензингер, Моника Раух (1998), «Параметрические и кинетические минимальные остовные деревья», 39-й ежегодный симпозиум по основам информатики, FOCS '98, 8–11 ноября 1998 г., Пало-Альто, Калифорния, США (PDF) , Компьютерное общество IEEE , стр. 596–605, doi : 10.1109/SFCS.1998.743510 , S2CID 2559456
^ Рахмати, Захед; Зарей, Алиреза (2012), «Кинетическое евклидово минимальное остовное дерево на плоскости», Журнал дискретных алгоритмов , 16 : 2–11, doi : 10.1016/j.jda.2012.04.009 , MR 2960341
^ Jump up to: Перейти обратно: ^а ^б Рахмати, Захед; Абам, Мохаммед Али; Кинг, Валери ; Уайтсайдс, Сью ; Зарей, Алиреза (2015), «Простой и быстрый метод решения кинетических задач близости», Computational Geometry: Theory & Applications , 48 (4): 342–359, arXiv : 1311.2032 , doi : 10.1016/j.comgeo.2014.12.002 , МР 3296072 , S2CID 18971251
^ Меулеманс, Воутер; Шпекманн, Беттина ; Вербек, Кевин; Вулмс, Жюль (2018), «Основы стабильности алгоритмов и их применение к кинетическим евклидовым MST», в Бендере, Майкл А.; Фарах-Колтон, Мартин ; Мостейро, Мигель А. (ред.), LATIN 2018: Теоретическая информатика – 13-й Латиноамериканский симпозиум, Буэнос-Айрес, Аргентина, 16–19 апреля 2018 г., Труды , Конспекты лекций по информатике, том. 10807, Springer, стр. 805–819, doi : 10.1007/978-3-319-77404-6_58 , ISBN. 978-3-319-77403-9 , S2CID 4709616
^ Яо, Эндрю Чи-Чи (1991), «Нижние границы для деревьев алгебраических вычислений с целочисленными входными данными», SIAM Journal on Computing , 20 (4): 655–668, doi : 10.1137/0220041 , MR 1105929
^ Грэм, РЛ ; Черт, Павол (1985), «К истории проблемы минимального остовного дерева», IEEE Annals of the History of Computing , 7 (1): 43–57, doi : 10.1109/mahc.1985.10011 , MR 0783327 , S2CID 10555375
^ Лоберман, Х.; Вайнбергер, А. (октябрь 1957 г.), «Формальные процедуры подключения клемм с минимальной общей длиной провода», Журнал ACM , 4 (4): 428–437, doi : 10.1145/320893.320896 , S2CID 7320964
^ Ву, Бин; Ю, Байлан; У, Цюшэн; Чен, Цзуоци; Яо, Шэньцзюнь; Хуан, Ян; Ву, Цзяньпин (октябрь 2017 г.), «Расширенный метод минимального остовного дерева для характеристики местных городских моделей», Международный журнал географической информатики , 32 (3): 450–475, doi : 10.1080/13658816.2017.1384830 , S2CID 46772272
^ Зан, Коннектикут (1973), «Использование минимального остовного дерева для распознавания пунктирных и пунктирных кривых» , 1-й Международный симпозиум по вычислительной технике, Давос, Швейцария, 4–7 сентября 1973 г.
^ Ли, Ин-Квон (2000), «Реконструкция кривой по неорганизованным точкам», Компьютерное геометрическое проектирование , 17 (2): 161–177, CiteSeerX 10.1.1.56.1432 , doi : 10.1016/S0167-8396(99)00044- 8 , МР 1733203
^ Барталь, Яир; Готлиб, Ли-Ад (2013), «Схема аппроксимации линейного времени для евклидовой TSP», 54-й ежегодный симпозиум IEEE по основам информатики, FOCS 2013, 26–29 октября 2013 г., Беркли, Калифорния, США , стр. 698– 706, CiteSeerX 10.1.1.409.1291 , doi : 10.1109/FOCS.2013.80 , MR 3246273 , S2CID 17514182
^ Ван, П.-Дж.; Кэлинеску, Г.; Ли, X.-Y.; Фридер, О. (2002), «Вещание с минимальным энергопотреблением в статических специальных беспроводных сетях», Wireless Networks , 8 (6): 607–617, doi : 10.1023/a:1020381720601 , S2CID 1297518
^ Клементи, Андреа Э.Ф.; Хуэйбан, Гурван; Росси, Джанлука; Верховен, Янн К.; Пенна, Паоло (2003 г.), «О коэффициенте аппроксимации эвристики на основе MST для проблемы энергоэффективного вещания в статических специальных радиосетях», 17-й Международный симпозиум по параллельной и распределенной обработке (IPDPS 2003), 22-26 апреля. 2003, Ницца, Франция, Труды Компьютерного общества IEEE, с. 222, номер документа : 10.1109/IPDPS.2003.1213407 , S2CID 17863487
^ Фламмини, Микеле; Класинг, Ральф; Наварра, Альфредо; Переннес, Стефан (2007), «Улучшенные результаты аппроксимации для задачи вещания с минимальной энергией», Algorithmica , 49 (4): 318–336, doi : 10.1007/s00453-007-9077-7 , MR 2358524 , S2CID 11982404
^ Амбюль, Кристоф (2005), «Оптимальная граница для алгоритма MST для вычисления энергоэффективных деревьев вещания в беспроводных сетях», в Кайресе, Луис; Итальяно, Джузеппе Ф .; Монтейро, Луис; Паламидесси, Катусия ; Юнг, Моти (ред.), Автоматы, языки и программирование, 32-й международный коллоквиум, ICALP 2005, Лиссабон, Португалия, 11–15 июля 2005 г., Труды , конспекты лекций по информатике, том. 3580, Springer, стр. 1139–1150, doi : 10.1007/11523468_92 , ISBN. 978-3-540-27580-0
^ Идс, Питер ; Уайтсайдс, Сью (1996), «Проблема реализации евклидовых минимальных остовных деревьев NP-трудна», Algorithmica , 16 (1): 60–82, doi : 10.1007/s004539900037 , MR 1394494
^ Анджелини, Патрицио; Брукдорфер, Тилль; Кьеза, Марко; Фрати, Фабрицио; Кауфманн, Майкл; Скуарселла, Клаудио (2014), «О требованиях к площади евклидовых минимальных остовных деревьев», Computational Geometry: Theory and Applications , 47 (2, часть B): 200–213, doi : 10.1016/j.comgeo.2012.10.011 , МР 3123788

Внешние ссылки

Учебное пособие по EMST , по mlpack документация

[gowros-1] Jump up to: Перейти обратно: ^а ^б Гауэр, Дж. К.; Росс, GJS (1969), «Минимальные остовные деревья и кластерный анализ с одной связью», Applied Статистика , 18 (1): 54–61, doi : 10.2307/2346439 , JSTOR 2346439 , MR 0242315

[shahoe-2] Jump up to: Перейти обратно: ^а ^б ^с ^д Шамос, Майкл Ян ; Хоуи, Дэн (1975), «Задачи ближайшей точки», 16-й ежегодный симпозиум по основам информатики, Беркли, Калифорния, США, 13–15 октября 1975 г. , Компьютерное общество IEEE, стр. 151–162, doi : 10.1109/ SFCS.1975.8 , MR 0426498 , S2CID 40615455

[bdek-3] Бозе, Просенджит ; Деврой, Люк ; Эванс, Уильям; Киркпатрик, Дэвид (2006), «Об отношении охвата графов Габриэля и β-скелетов», SIAM Journal on Discrete Mathematics , 20 (2): 412–427, doi : 10.1137/S0895480197318088 , MR 2257270

[aesw-4] Jump up to: Перейти обратно: ^а ^б ^с ^д Агарвал, ПК ; Эдельсбруннер, Х. ; Шварцкопф, О .; Вельцль, Э. (1991), «Евклидовы минимальные остовные деревья и бихроматические ближайшие пары», Discrete & Computational Geometry , 6 (1), Springer: 407–422, doi : 10.1007/BF02574698 , MR 1115099

[mrg-5] Jump up to: Перейти обратно: ^а ^б ^с Марч, Уильям Б.; Рам, Парикшит; Грей, Александр Г. (2010), «Быстрое евклидово минимальное остовное дерево: алгоритм, анализ и приложения», Рао, Бхарат; Кришнапурам, Баладжи; Томкинс, Эндрю; Ян, Цян (ред.), Труды 16-й Международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных, Вашингтон, округ Колумбия, США, 25–28 июля 2010 г. , стр. 603–612, doi : 10.1145/1835804.1835882 , S2CID 186025

[clarkson-6] Jump up to: Перейти обратно: ^а ^б Кларксон, Кеннет Л. (1989), «Алгоритм для геометрических минимальных остовных деревьев, требующий почти линейного ожидаемого времени», Algorithmica , 4 (1–4): 461–469, doi : 10.1007/BF01553902 , MR 1019387 , S2CID 22176641

[monsur-7] Jump up to: Перейти обратно: ^а ^б ^с ^д Монма, Клайд; Сури, Субхаш (1992), «Переходы в геометрических минимальных остовных деревьях», Дискретная и вычислительная геометрия , 8 (3): 265–293, doi : 10.1007/BF02293049 , MR 1174358 , S2CID 30101649

[nzz-8] Jump up to: Перейти обратно: ^а ^б Нарасимхан, Гири; Захариасен, Мартин; Чжу, Цзяньлинь (2000), «Эксперименты с вычислением геометрических минимальных остовных деревьев», Материалы 2-го семинара по разработке алгоритмов и экспериментам , стр. 183–196.

[frakau-9] Jump up to: Перейти обратно: ^а ^б Фрати, Фабрицио; Кауфманн, Майкл (2011), «Границы полиномиальной области для вложений деревьев MST», Вычислительная геометрия: теория и приложения , 44 (9): 529–543, doi : 10.1016/j.comgeo.2011.05.005 , MR 2819643 , S2CID 5634139

[king-10] Jump up to: Перейти обратно: ^а ^б Кинг, Джеймс А. (2006), «Реализация минимальных остовных деревьев степени 10 в трехмерном пространстве» (PDF) , Материалы 18-й ежегодной канадской конференции по вычислительной геометрии, CCCG 2006, 14–16 августа 2006 г., Королевский университет, Онтарио, Канада , стр. 39–42.

[kln-11] Jump up to: Перейти обратно: ^а ^б Крзнарич, Драго; Левкопулос, Христос; Нильссон, Бенгт Дж. (1999), "Минимум пролетных деревьев в $d$ Dimensions», Nordic Journal of Computing , 6 (4): 446–461, MR 1736451. Эта версия этой статьи недоступна в Интернете; вместо этого см. версию той же статьи, опубликованную на конференции 1997 года, дои : 10.1007/3-540-63397-9_26 .

[gilpol-12] Jump up to: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Гилберт, EN ; Поллак, Х.О. (1968), «Минимальные деревья Штейнера», SIAM Journal on Applied Mathematics , 16 (1): 1–29, doi : 10.1137/0116001 , JSTOR 2099400 , MR 0223269

[eppstein-13] Jump up to: Перейти обратно: ^а ^б ^с ^д Эппштейн, Дэвид (1999), «Соединительные деревья и гаечные ключи» (PDF) , в Саке, Ж.-Р. ; Уррутиа, Дж. (ред.), Справочник по вычислительной геометрии , Elsevier, стр. 425–461, MR 1746681.

[1steiner-14] Георгакопулос, Джордж; Пападимитриу, Христос Х. (1987), «Проблема дерева 1 Штейнера», Журнал алгоритмов , 8 (1): 122–130, doi : 10.1016/0196-6774(87)90032-0 , MR 0875330

[robsal-15] Jump up to: Перейти обратно: ^а ^б Робинс, Г.; Салове, Дж. С. (1995), «Минимальные остовные деревья низкой степени», Дискретная и вычислительная геометрия , 14 (2): 151–165, doi : 10.1007/BF02570700 , MR 1331924 , S2CID 16040977

[kissing-16] Пфендер, Флориан; Циглер, Гюнтер М. (сентябрь 2004 г.), «Целующиеся числа, упаковки сфер и некоторые неожиданные доказательства» (PDF) , Уведомления Американского математического общества : 873–883

[sse-17] Стил, Дж. Майкл ; Шепп, Лоуренс А.; Эдди, Уильям Ф. (1987), «О количестве листьев евклидова минимального остовного дерева», Journal of Applied Probability , 24 (4): 809–826, doi : 10.2307/3214207 , JSTOR 3214207 , MR 0913823 , S2CID 29026025

[presha-18] Препарата, Франко П .; Шамос, Майкл Ян (1985), Вычислительная геометрия: Введение , Тексты и монографии по информатике, Springer-Verlag, Нью-Йорк, стр. 263, номер домена : 10.1007/978-1-4612-1098-6 , ISBN. 0-387-96131-3 , МР 0805539 , S2CID 206656565

[comment-19] Туссен, GT (1980), «Комментарий: Алгоритмы вычисления графа относительной окрестности», Electronics Letters , 16 (22): 860, Bibcode : 1980ElL....16..860T , doi : 10.1049/el:19800611 ; ответ Уркарта, стр. 860–861.

[yao82-20] Jump up to: Перейти обратно: ^а ^б ^с Яо, Эндрю Чи Чи (1982), «О построении минимальных остовных деревьев в $k$ -мерных пространствах и связанных проблемах», SIAM Journal on Computing , 11 (4): 721–736, doi : 10.1137/0211059 , MR 0677663

[bwy-21] Jump up to: Перейти обратно: ^а ^б Бентли, Джон Луис ; Вейде, Брюс В.; Яо, Эндрю К. (1980), «Алгоритмы оптимального ожидаемого времени для задач ближайшей точки» , Транзакции ACM в математическом программном обеспечении , 6 (4): 563–580, doi : 10.1145/355921.355927 , MR 0599977 , S2CID 17238717

[ss89-22] Стил, Дж. Майкл ; Снайдер, Тимоти Лоу (1989), «Темпы роста в наихудшем случае некоторых классических задач комбинаторной оптимизации» , SIAM Journal on Computing , 18 (2): 278–287, doi : 10.1137/0218019 , MR 0986667

[steele-23] Стил, Дж. Майкл (1988), «Темпы роста евклидовых минимальных остовных деревьев со взвешенными по мощности ребрами», Annals of Probability , 16 (4): 1767–1787, doi : 10.1214/aop/1176991596 , JSTOR 2243991 , MR 0958215

[penrose-24] Пенроуз, Мэтью Д. (1997), «Самое длинное ребро случайного минимального остовного дерева», Анналы прикладной вероятности , 7 (2): 340–361, doi : 10.1214/aoap/1034625335 , MR 1442317

[bgj78-25] Бойс, WM; Гэри, MR ; Джонсон, Д.С. (1978), «Заметка о разбиении минимальных остовных деревьев пополам», Networks , 8 (3): 187–192, doi : 10.1002/net.3230080302 , MR 0491324

[bm09-26] Jump up to: Перейти обратно: ^а ^б ^с Бучин, Кевин; Мульцер, Вольфганг (2011), «Триангуляции Делоне за $время O$ (сортировка ( $n$ )) и более», Журнал ACM , 58 (2): A6:1–A6:27, doi : 10.1145/1944345.1944347 , MR 2786587 , S2CID 11316974

[mares-27] Мареш, Мартин (2004), «Два алгоритма с линейным временем для MST на второстепенных классах замкнутых графов» (PDF) , Archivum Mathematicum , 40 (3): 315–320, MR 2107027

[devillers-28] Девиллерс, Оливье (1992), «Рандомизация дает простой $O (n log * n)$ алгоритмы для сложных $Ω(n)$ задач » (PDF) , Международный журнал вычислительной геометрии и приложений , 2 (1): 97–111, doi : 10.1142/S021819599200007X , MR 1159844 , S2CID 60203

[topp-29] О'Рурк, Дж .; Демейн, Э. (2001–2002), «Проблема 5: Евклидово минимальное остовное дерево» , Проект открытых проблем , Колледж Смита

[dwyer-30] Дуайер, Рекс А. (1991), «Многомерные диаграммы Вороного в линейном ожидаемом времени», Discrete & Computational Geometry , 6 (4): 343–367, doi : 10.1007/BF02574694 , MR 1098813

[kkt-31] Каргер, Дэвид Р .; Кляйн, Филип Н.; Тарьян, Роберт Э. (1995), «Рандомизированный алгоритм линейного времени для поиска минимальных остовных деревьев», Journal of the ACM , 42 (2): 321–328, doi : 10.1145/201019.201022 , MR 1409738 , S2CID 832583

[cck-32] Чаттерджи, С.; Коннор, М.; Кумар, П. (2010), «Геометрические минимальные охватывающие деревья с GeoFilterKruskal», в Фесте, Паола (ред.), Экспериментальные алгоритмы: 9-й Международный симпозиум, SEA 2010, остров Искья, Неаполь, Италия, 20-22 мая 2010 г., Труды , Конспекты лекций по информатике, вып. 6049, Springer-Verlag, стр. 486–500, номер документа : 10.1007/978-3-642-13193-6_41 , ISBN. 978-3-642-13192-9

[arymou-33] Арья, Сунил; Маунт, Дэвид М. (2016), «Быстрый и простой алгоритм вычисления приближенных евклидовых минимальных остовных деревьев», Краутгеймер, Роберт (редактор), Труды двадцать седьмого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам, SODA 2016 , Арлингтон, Вирджиния, США, 10–12 января 2016 г. , стр. 1220–1233, doi : 10.1137/1.9781611974331.ch85 , MR 3478461

[offline-34] Эппштейн, Дэвид (1994), «Автономные алгоритмы для динамических задач минимального остовного дерева» , Journal of Algorithms , 17 (2): 237–250, doi : 10.1006/jagm.1994.1033 , MR 1291541

[chadyn-35] Чан, Тимоти М. (2010), «Динамическая структура данных для трехмерных выпуклых оболочек и двумерных запросов к ближайшему соседу», Журнал ACM , 57 (3): Статья 16, doi : 10.1145/1706591.1706596 , MR 2665885 , S2CID 47454142

[extrema-36] Эппштейн, Дэвид (1995), «Динамические евклидовы минимальные остовные деревья и экстремумы бинарных функций», Discrete & Computational Geometry , 13 (1): 111–122, doi : 10.1007/BF02574030 , MR 1300511 , S2CID 7339165

[kti-37] Като, Н.; Токуяма, Т.; Ивано, К. (1995), «О минимальном и максимальном остовном дереве линейно движущихся точек», Discrete & Computational Geometry , 13 (2): 161–176, doi : 10.1007/BF02574035 , MR 1314960

[chalev-38] Чан, Тимоти М. (2003), «Об уровнях в расположении кривых», Discrete & Computational Geometry , 29 (3): 375–393, doi : 10.1007/s00454-002-2840-2 , MR 1961005 , S2CID 18966889

[rzcomb-39] Рахмати, Захед; Зарей, Алиреза (2010), «Комбинаторные изменения евклидова минимального остова дерева движущихся точек на плоскости» (PDF) , Материалы 22-й ежегодной канадской конференции по вычислительной геометрии, Виннипег, Манитоба, Канада, 9–11 августа 2010 г. , стр. 43–45

[abb-40] Акитая, Хьюго А.; Биниаз, Ахмад; Бозе, Просенджит ; Де Каруфель, Жан-Лу; Махешвари, Анил; да Силвейра, Луис Фернандо Шульц Ксавьер; Смид, Михил (2021), «Задача о минимальном движущемся остовном дереве», Любив, Анна ; Салаватипур, Мохаммад Р. (ред.), Алгоритмы и структуры данных: 17-й Международный симпозиум, WADS 2021, виртуальное мероприятие, 9–11 августа 2021 г., Материалы , конспекты лекций по информатике, том. 12808, Springer, стр. 15–28, doi : 10.1007/978-3-030-83508-8_2 , ISBN. 978-3-030-83507-1 , S2CID 234599877

[bgz-41] Баш, Жюльен; Гибас, Леонидас Дж .; Чжан, Ли (1997), «Проблемы близости движущихся точек», в Буассонна, Жан-Даниэль (ред.), Труды тринадцатого ежегодного симпозиума по вычислительной геометрии, Ницца, Франция, 4–6 июня 1997 г. , Ассоциация вычислительной техники. Machinery, стр. 344–351, doi : 10.1145/262839.262998 , S2CID 15556637.

[aegh-42] Агарвал, Панкадж К .; Эппштейн, Дэвид ; Гибас, Леонидас Дж .; Хензингер, Моника Раух (1998), «Параметрические и кинетические минимальные остовные деревья», 39-й ежегодный симпозиум по основам информатики, FOCS '98, 8–11 ноября 1998 г., Пало-Альто, Калифорния, США (PDF) , Компьютерное общество IEEE , стр. 596–605, doi : 10.1109/SFCS.1998.743510 , S2CID 2559456

[rzkin-43] Рахмати, Захед; Зарей, Алиреза (2012), «Кинетическое евклидово минимальное остовное дерево на плоскости», Журнал дискретных алгоритмов , 16 : 2–11, doi : 10.1016/j.jda.2012.04.009 , MR 2960341

[rakwz-44] Jump up to: Перейти обратно: ^а ^б Рахмати, Захед; Абам, Мохаммед Али; Кинг, Валери ; Уайтсайдс, Сью ; Зарей, Алиреза (2015), «Простой и быстрый метод решения кинетических задач близости», Computational Geometry: Theory & Applications , 48 (4): 342–359, arXiv : 1311.2032 , doi : 10.1016/j.comgeo.2014.12.002 , МР 3296072 , S2CID 18971251

[msvw-45] Меулеманс, Воутер; Шпекманн, Беттина ; Вербек, Кевин; Вулмс, Жюль (2018), «Основы стабильности алгоритмов и их применение к кинетическим евклидовым MST», в Бендере, Майкл А.; Фарах-Колтон, Мартин ; Мостейро, Мигель А. (ред.), LATIN 2018: Теоретическая информатика – 13-й Латиноамериканский симпозиум, Буэнос-Айрес, Аргентина, 16–19 апреля 2018 г., Труды , Конспекты лекций по информатике, том. 10807, Springer, стр. 805–819, doi : 10.1007/978-3-319-77404-6_58 , ISBN. 978-3-319-77403-9 , S2CID 4709616

[yao89-46] Яо, Эндрю Чи-Чи (1991), «Нижние границы для деревьев алгебраических вычислений с целочисленными входными данными», SIAM Journal on Computing , 20 (4): 655–668, doi : 10.1137/0220041 , MR 1105929

[history-47] Грэм, РЛ ; Черт, Павол (1985), «К истории проблемы минимального остовного дерева», IEEE Annals of the History of Computing , 7 (1): 43–57, doi : 10.1109/mahc.1985.10011 , MR 0783327 , S2CID 10555375

[lobwei-48] Лоберман, Х.; Вайнбергер, А. (октябрь 1957 г.), «Формальные процедуры подключения клемм с минимальной общей длиной провода», Журнал ACM , 4 (4): 428–437, doi : 10.1145/320893.320896 , S2CID 7320964

[urban-49] Ву, Бин; Ю, Байлан; У, Цюшэн; Чен, Цзуоци; Яо, Шэньцзюнь; Хуан, Ян; Ву, Цзяньпин (октябрь 2017 г.), «Расширенный метод минимального остовного дерева для характеристики местных городских моделей», Международный журнал географической информатики , 32 (3): 450–475, doi : 10.1080/13658816.2017.1384830 , S2CID 46772272

[zahn-50] Зан, Коннектикут (1973), «Использование минимального остовного дерева для распознавания пунктирных и пунктирных кривых» , 1-й Международный симпозиум по вычислительной технике, Давос, Швейцария, 4–7 сентября 1973 г.

[lee-51] Ли, Ин-Квон (2000), «Реконструкция кривой по неорганизованным точкам», Компьютерное геометрическое проектирование , 17 (2): 161–177, CiteSeerX 10.1.1.56.1432 , doi : 10.1016/S0167-8396(99)00044- 8 , МР 1733203

[bargot-52] Барталь, Яир; Готлиб, Ли-Ад (2013), «Схема аппроксимации линейного времени для евклидовой TSP», 54-й ежегодный симпозиум IEEE по основам информатики, FOCS 2013, 26–29 октября 2013 г., Беркли, Калифорния, США , стр. 698– 706, CiteSeerX 10.1.1.409.1291 , doi : 10.1109/FOCS.2013.80 , MR 3246273 , S2CID 17514182

[wclf-53] Ван, П.-Дж.; Кэлинеску, Г.; Ли, X.-Y.; Фридер, О. (2002), «Вещание с минимальным энергопотреблением в статических специальных беспроводных сетях», Wireless Networks , 8 (6): 607–617, doi : 10.1023/a:1020381720601 , S2CID 1297518

[chrvp-54] Клементи, Андреа Э.Ф.; Хуэйбан, Гурван; Росси, Джанлука; Верховен, Янн К.; Пенна, Паоло (2003 г.), «О коэффициенте аппроксимации эвристики на основе MST для проблемы энергоэффективного вещания в статических специальных радиосетях», 17-й Международный симпозиум по параллельной и распределенной обработке (IPDPS 2003), 22-26 апреля. 2003, Ницца, Франция, Труды Компьютерного общества IEEE, с. 222, номер документа : 10.1109/IPDPS.2003.1213407 , S2CID 17863487

[fknp-55] Фламмини, Микеле; Класинг, Ральф; Наварра, Альфредо; Переннес, Стефан (2007), «Улучшенные результаты аппроксимации для задачи вещания с минимальной энергией», Algorithmica , 49 (4): 318–336, doi : 10.1007/s00453-007-9077-7 , MR 2358524 , S2CID 11982404

[ambuhl-56] Амбюль, Кристоф (2005), «Оптимальная граница для алгоритма MST для вычисления энергоэффективных деревьев вещания в беспроводных сетях», в Кайресе, Луис; Итальяно, Джузеппе Ф .; Монтейро, Луис; Паламидесси, Катусия ; Юнг, Моти (ред.), Автоматы, языки и программирование, 32-й международный коллоквиум, ICALP 2005, Лиссабон, Португалия, 11–15 июля 2005 г., Труды , конспекты лекций по информатике, том. 3580, Springer, стр. 1139–1150, doi : 10.1007/11523468_92 , ISBN. 978-3-540-27580-0

[ew94-57] Идс, Питер ; Уайтсайдс, Сью (1996), «Проблема реализации евклидовых минимальных остовных деревьев NP-трудна», Algorithmica , 16 (1): 60–82, doi : 10.1007/s004539900037 , MR 1394494

[abcfks-58] Анджелини, Патрицио; Брукдорфер, Тилль; Кьеза, Марко; Фрати, Фабрицио; Кауфманн, Майкл; Скуарселла, Клаудио (2014), «О требованиях к площади евклидовых минимальных остовных деревьев», Computational Geometry: Theory and Applications , 47 (2, часть B): 200–213, doi : 10.1016/j.comgeo.2012.10.011 , МР 3123788

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]