Диаграмма влияния

Не путать с бинарной диаграммой решений .

Диаграмма влияния ( ID ) (также называемая диаграммой релевантности , диаграммой решений или сетью решений ) — это компактное графическое и математическое представление ситуации принятия решения. Это обобщение байесовской сети , в которой вероятностного вывода, не только задачи но и проблемы принятия решений (в соответствии с критерием максимальной ожидаемой полезности можно моделировать и решать ).

ID был впервые разработан в середине 1970-х годов аналитиками решений с интуитивно понятной семантикой, которую легко понять. В настоящее время оно широко применяется и становится альтернативой дереву решений , которое обычно страдает от экспоненциального роста числа ветвей с каждой моделируемой переменной. ID напрямую применим при анализе командных решений , поскольку он позволяет моделировать и решать неполный обмен информацией между членами команды. Расширения ID также находят свое применение в теории игр в качестве альтернативного представления дерева игры .

Семантика

ID — это ориентированный ациклический граф с тремя типами (плюс одним подтипом) узла и тремя типами дуг (или стрелок) между узлами.

Узлы:

• решения Узел (соответствующий каждому принимаемому решению) изображается в виде прямоугольника.
• неопределенности Узел (соответствующий каждой моделируемой неопределенности) изображается в виде овала.

• Детерминированный узел (соответствующий особому виду неопределенности, при котором его результат детерминированно известен всякий раз, когда известен результат некоторых других неопределенностей) изображается в виде двойного овала.

• Узел значения (соответствующий каждому компоненту аддитивно разделимой функции полезности Фон Неймана-Моргенштерна ) изображается в виде восьмиугольника (или ромба).

Дуги:

• Функциональные дуги (оканчивающиеся узлом значения) указывают на то, что один из компонентов аддитивно разделимой функции полезности является функцией всех узлов на их хвостах.
• Условные дуги (оканчивающиеся узлом неопределенности) указывают, что неопределенность в их головах вероятностно обусловлена ​​во всех узлах в их хвостах.

• Условные дуги (оканчивающиеся детерминированным узлом) указывают, что неопределенность в их головах детерминированно обусловлена ​​всеми узлами в их хвостах.

• Информационные дуги (заканчивающиеся узлом решения) указывают, что решение в их головах принимается с заранее известными результатами всех узлов в их хвостах.

Учитывая правильно структурированный идентификатор:

• Узлы принятия решений и входящие информационные дуги вместе определяют альтернативы (что можно сделать, если результат определенных решений и/или неопределенности известны заранее).
• Узлы неопределенности/детерминированности и входящие условные дуги совместно моделируют информацию (то, что известно, и их вероятностные/детерминированные отношения).
• Узлы ценностей и входящие функциональные дуги в совокупности определяют количественное предпочтение (насколько вещи предпочтительнее друг друга).

Альтернатива, информация и предпочтение в анализе решений называются основой принятия решений . Они представляют собой три необходимых компонента любой действительной ситуации принятия решения.

Формально семантика диаграммы влияния основана на последовательном построении узлов и дуг, что предполагает указание всех условных зависимостей в диаграмме. Спецификация определяется $d$-критерий разделения байесовской сети. Согласно этой семантике, каждый узел вероятностно независимо от своих узлов, не являющихся преемниками, с учетом результатов своих непосредственных узлов-предшественников. Аналогично, отсутствует дуга между узлом, не имеющим значения. $X$ и незначительный узел $Y$ подразумевает, что существует набор узлов, не имеющих значений $Z$, например, родители $Y$, что делает $Y$ независимый от $X$ учитывая результат узлов в $Z$.

Пример

Простая диаграмма влияния для принятия решения об отпуске

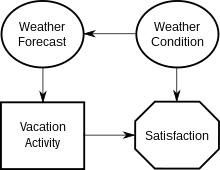
Рассмотрим простую диаграмму влияния, представляющую ситуацию, когда лицо, принимающее решение, планирует свой отпуск.

• Существует 1 узел принятия решения ( Отпускная деятельность ), 2 узла неопределенности ( Погодные условия, Прогноз погоды ) и 1 узел значения ( Удовлетворенность ).
• Есть 2 функциональные дуги (заканчивающиеся « Удовлетворением »), 1 условная дуга (заканчивающаяся «Прогнозом погоды ») и 1 информационная дуга (заканчивающаяся «Активностью в отпуске» ).

• Функциональные дуги, оканчивающиеся на «Удовлетворение», указывают на то, что «Удовлетворение» является функцией полезности погодных условий и активности во время отпуска . Другими словами, их удовлетворенность можно измерить количественно, если они знают, какая погода и какой вид деятельности они выбирают. (Обратите внимание, что они не оценивают прогноз погоды напрямую)
• Условное окончание дуги в «Прогнозе погоды» указывает на их убежденность в том, что прогноз погоды и погодные условия могут быть зависимыми.
• Информационная дуга, заканчивающаяся «Активностью в отпуске», они будут знать только прогноз погоды , а не погодные условия указывает на то, что при выборе . Другими словами, реальная погода будет известна после того, как они сделают свой выбор, и на данном этапе они могут рассчитывать только на прогноз.

• Из этого также семантически следует, например, что деятельность в отпуске не зависит от погодных условий (не имеет отношения к ним), если прогноз погоды . известен

Применимость к ценности информации

Приведенный выше пример подчеркивает силу диаграммы влияния в представлении чрезвычайно важной концепции анализа решений, известной как ценность информации . Рассмотрим следующие три сценария;

• Сценарий 1: Лицо, принимающее решения, может принять решение о проведении отпуска, зная, какими погодные условия будут . Это соответствует добавлению дополнительной информационной дуги от погодных условий к активности в отпуске на приведенной выше диаграмме влияния.
• Сценарий 2: Исходная диаграмма влияния, показанная выше.
• Сценарий 3: Лицо, принимающее решения, принимает решение, даже не зная прогноза погоды . Это соответствует удалению информационной дуги от прогноза погоды до активности в отпуске на приведенной выше диаграмме влияния.

Сценарий 1 является наилучшим из возможных сценариев для этой ситуации принятия решения, поскольку больше нет никакой неопределенности в отношении того, что их волнует ( погодные условия ) при принятии решения. Сценарий 3, однако, является наихудшим из возможных сценариев для этой ситуации принятия решения, поскольку им нужно принять решение без какого-либо намека ( Прогноз погоды ) на то, что их волнует ( Погодные условия ).

Лицу, принимающему решения, обычно лучше (в среднем определенно не хуже) перейти от сценария 3 к сценарию 2 за счет получения новой информации. Максимум, что они должны быть готовы заплатить за такой шаг, называется ценностью информации о прогнозе погоды , которая, по сути, представляет собой ценность несовершенной информации о погодных условиях .

Применимость этого простого идентификатора и ценность концепции информации огромны, особенно при принятии медицинских решений , когда большинство решений приходится принимать на основе неполной информации о пациентах, заболеваниях и т. д.

Связанные понятия

Диаграммы влияния являются иерархическими и могут быть определены либо с точки зрения их структуры, либо более подробно с точки зрения функционального и числового отношения между элементами диаграммы. Идентификатор, который последовательно определен на всех уровнях — структуре, функции и числе, — представляет собой четко определенное математическое представление и называется хорошо сформированной диаграммой влияния (WFID). WFID можно оценивать с помощью операций обращения и удаления, чтобы получить ответы на большой класс вероятностных, логических вопросов и вопросов принятия решений. Более поздние методы были разработаны исследователями искусственного интеллекта, касающимися вывода байесовской сети ( распространения убеждений ).

Диаграмма влияния, имеющая только узлы неопределенности (т. е. байесовская сеть), также называется диаграммой релевантности . Дуга, соединяющая узел A с B, подразумевает не только то, что « A релевантно B », но также и то, что « B релевантно A » (т. е. релевантность — это симметричные отношения).

См. также

• Байесовская сеть
• Бинарная диаграмма решений
• Программное обеспечение для принятия решений
• Дерево решений
• Диаграмма «рыбья кость»
• Блок-схема
• Морфологический анализ

Библиография

• Детварасити, А.; Шахтер, Р.Д. (декабрь 2005 г.). «Диаграммы влияния для анализа командных решений» (PDF) . Анализ решений . 2 (4): 207–228. дои : 10.1287/дека.1050.0047 .
• Хольцман, Сэмюэл (1988). Интеллектуальные системы принятия решений . Аддисон-Уэсли. ISBN  978-0-201-11602-1 .
• Ховард, Р.А. и Дж.Э. Мэтисон, «Диаграммы влияния» (1981), в «Чтениях по принципам и применениям анализа решений» , ред. Р. А. Ховард и Дж. Э. Мэтисон, Vol. II (1984), Менло-Парк, Калифорния: Группа стратегических решений.
• Коллер, Д.; Мильч, Б. (октябрь 2003 г.). «Диаграммы мультиагентного влияния для представления и решения игр» (PDF) . Игры и экономическое поведение . 45 : 181–221. дои : 10.1016/S0899-8256(02)00544-4 .
• Перл, Иудея (1988). Вероятностные рассуждения в интеллектуальных системах: сети правдоподобных выводов . Серия «Представление и рассуждение». Сан-Матео, Калифорния: Морган Кауфманн. ISBN  0-934613-73-7 .
• Шахтер, Р.Д. (ноябрь – декабрь 1986 г.). «Оценка диаграмм влияния» (PDF) . Исследование операций . 34 (6): 871–882. дои : 10.1287/опре.34.6.871 .
• Шахтер, Р.Д. (июль – август 1988 г.). «Вероятностный вывод и диаграммы влияния» (PDF) . Исследование операций . 36 (4): 589–604. дои : 10.1287/опре.36.4.589 . hdl : 10338.dmlcz/135724 .
• Вирин, Лев; Трампер, Майкл (2008). Решения проекта: Искусство и наука . Вена, Вирджиния: Концепции управления. ISBN  978-1-56726-217-9 .
• Перл, Дж. (1985). Байесовские сети: модель самоактивируемой памяти для доказательного рассуждения (Технический отчет Калифорнийского университета в Лос-Анджелесе CSD-850017) . Материалы седьмой ежегодной конференции Общества когнитивных наук, 15–17 апреля 1985 г. http://ftp.cs.ucla.edu/tech-report/198_-reports/850017.pdf ., Калифорнийский университет, Ирвин, Калифорния. стр. 329–334 . Проверено 1 мая 2010 г. {{cite conference}}: Внешняя ссылка в |conference= ( помощь )

Внешние ссылки

• Что такое диаграммы влияния?
• Перл, Дж. (декабрь 2005 г.). «Диаграммы влияния — исторические и личные перспективы» (PDF) . Анализ решений . 2 (4): 232–4. дои : 10.1287/дека.1050.0055 .