Потеря Хубера

В статистике — потери Хубера это функция потерь , используемая в устойчивой регрессии , которая менее чувствительна к выбросам в данных, чем потеря в квадрате ошибки . Иногда используется вариант классификации.

Определение

Функция потерь Хубера описывает штраф, наносимый процедурой оценки $f$ . Хубер (1964) определяет функцию потерь кусочно по формуле ^[1]

L_{\delta }(a)={\begin{cases}{\frac {1}{2}}{a^{2}}&{\text{for }}|a|\leq \delta ,\\\delta \cdot \left(|a|-{\frac {1}{2}}\delta \right),&{\text{otherwise.}}\end{cases}}

Эта функция является квадратичной для малых значений $a$ и линейной для больших значений с одинаковыми значениями и наклонами различных сечений в двух точках, где $|a|=\delta$ . Переменная $a$ часто относится к остаткам, то есть к разнице между наблюдаемыми и прогнозируемыми значениями. $a=y-f(x)$ , поэтому первое можно расширить до ^[2]

L_{\delta }(y,f(x))={\begin{cases}{\frac {1}{2}}(y-f(x))^{2}&{\text{for }}|y-f(x)|\leq \delta ,\\\delta \ \cdot \left(|y-f(x)|-{\frac {1}{2}}\delta \right),&{\text{otherwise.}}\end{cases}}

Потери Хубера — это свертка функции абсолютного значения с прямоугольной функцией , масштабированной и преобразованной. Таким образом, он «сглаживает» угол первого в начале координат.

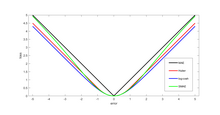
Мотивация

Двумя наиболее часто используемыми функциями потерь являются квадрат потерь , $L(a)=a^{2}$ и абсолютная потеря , $L(a)=|a|$ . Функция квадратичных потерь дает среднеарифметическую несмещенную оценку , а функция потерь абсолютного значения дает несмещенную медианную оценку (в одномерном случае и геометрическую медианно- несмещенную оценку для многомерного случая). Квадрат потерь имеет тот недостаток, что в нем доминируют выбросы — при суммировании по набору $a$ 's (как в ${\textstyle \sum _{i=1}^{n}L(a_{i})}$ ), на выборочное среднее слишком сильно влияют несколько особенно крупных $a$ -значения, когда распределение имеет тяжелый хвост: с точки зрения теории оценивания асимптотическая относительная эффективность среднего значения низкая для распределений с тяжелым хвостом.

Как определено выше, функция потерь Хубера сильно выпукла в равномерной окрестности своего минимума. $a=0$ ; на границе этой однородной окрестности функция потерь Хубера имеет дифференцируемое продолжение до аффинной функции в точках $a=-\delta$ и $a=\delta$ . Эти свойства позволяют ему сочетать большую часть чувствительности несмещенной к среднему оценки среднего значения с минимальной дисперсией (с использованием квадратичной функции потерь) и надежность несмещенной к среднему оценки (с использованием функции абсолютного значения).

Функция потерь псевдо-Хубера

Функция потерь Псевдо-Хьюбера может использоваться как плавная аппроксимация функции потерь Хубера. Он сочетает в себе лучшие свойства L2 квадрата потерь и L1 абсолютных потерь , будучи сильно выпуклым, когда он близок к целевому/минимуму, и менее крутым для экстремальных значений. Масштаб, в котором функция потерь Псевдо-Хьюбера переходит от потерь L2 для значений, близких к минимуму, к потерям L1 для экстремальных значений, а крутизну при экстремальных значениях можно контролировать с помощью $\delta$ ценить. Функция потерь Псевдо-Хьюбера гарантирует, что производные непрерывны для всех степеней. Это определяется как ^[3]^[4]

L_{\delta }(a)=\delta ^{2}\left({\sqrt {1+(a/\delta )^{2}}}-1\right).

Таким образом, эта функция аппроксимирует $a^{2}/2$ для небольших значений $a$ , и аппроксимирует прямую линию с наклоном $\delta$ для больших значений $a$ .

Хотя приведенная выше форма является наиболее распространенной, существуют и другие гладкие аппроксимации функции потерь Хубера. ^[5]

Вариант классификации

В целях классификации вариант потерь Хубера, называемый модифицированным Хубером иногда используется . Учитывая предсказание $f(x)$ (реальная оценка классификатора) и истинная метка двоичного класса $y\in \{+1,-1\}$ модифицированные потери Хубера определяются как ^[6]

L(y,f(x))={\begin{cases}\max(0,1-y\,f(x))^{2}&{\textrm {for}}\,\,y\,f(x)>-1,\\-4y\,f(x)&{\textrm {otherwise.}}\end{cases}}

Термин $\max(0,1-y\,f(x))$ — потери на шарнирах , используемые в машинах опорных векторов ; квадратично сглаженная шарнирная потеря является обобщением $L$ . ^[6]

Приложения

Функция потерь Хубера используется в робастной статистике , M-оценке и аддитивном моделировании . ^[7]

См. также

Ссылки

^ Хубер, Питер Дж . (1964). «Надежная оценка параметра местоположения» . Анналы статистики . 53 (1): 73–101. дои : 10.1214/aoms/1177703732 . JSTOR 2238020 .
^ Хасти, Тревор; Тибширани, Роберт; Фридман, Джером (2009). Элементы статистического обучения . п. 349. Архивировано из оригинала 26 января 2015 г. По сравнению с Hastie et al. , потери масштабируются с коэффициентом ⁠ 1 / 2 ⁠ , чтобы соответствовать первоначальному определению Хубера, данному ранее.
^ Шарбонье, П.; Блан-Феро, Л .; Обер, Г.; Барло, М. (1997). «Детерминированная регуляризация с сохранением краев в компьютерных изображениях». IEEE Транс. Процесс изображения . 6 (2): 298–311. Бибкод : 1997ITIP....6..298C . CiteSeerX 10.1.1.64.7521 . дои : 10.1109/83.551699 . ПМИД 18282924 .
^ Хартли, Р.; Зиссерман, А. (2003). Множественная геометрия в компьютерном зрении (2-е изд.). Издательство Кембриджского университета. п. 619 . ISBN 978-0-521-54051-3 .
^ Ланге, К. (1990). «Сходимость алгоритмов восстановления изображений со сглаживанием Гиббса». IEEE Транс. Мед. Изображение . 9 (4): 439–446. дои : 10.1109/42.61759 . ПМИД 18222791 .
^ Jump up to: ^а ^б Чжан, Тонг (2004). Решение крупномасштабных задач линейного прогнозирования с использованием алгоритмов стохастического градиентного спуска . ИКМЛ.
^ Фридман, Дж. Х. (2001). «Аппроксимация жадными функциями: машина повышения градиента» . Анналы статистики . 26 (5): 1189–1232. дои : 10.1214/aos/1013203451 . JSTOR 2699986 .

[1] Хубер, Питер Дж . (1964). «Надежная оценка параметра местоположения» . Анналы статистики . 53 (1): 73–101. дои : 10.1214/aoms/1177703732 . JSTOR 2238020 .

[2] Хасти, Тревор; Тибширани, Роберт; Фридман, Джером (2009). Элементы статистического обучения . п. 349. Архивировано из оригинала 26 января 2015 г. По сравнению с Hastie et al. , потери масштабируются с коэффициентом ⁠ 1 / 2 ⁠ , чтобы соответствовать первоначальному определению Хубера, данному ранее.

[3] Шарбонье, П.; Блан-Феро, Л .; Обер, Г.; Барло, М. (1997). «Детерминированная регуляризация с сохранением краев в компьютерных изображениях». IEEE Транс. Процесс изображения . 6 (2): 298–311. Бибкод : 1997ITIP....6..298C . CiteSeerX 10.1.1.64.7521 . дои : 10.1109/83.551699 . ПМИД 18282924 .

[4] Хартли, Р.; Зиссерман, А. (2003). Множественная геометрия в компьютерном зрении (2-е изд.). Издательство Кембриджского университета. п. 619 . ISBN 978-0-521-54051-3 .

[5] Ланге, К. (1990). «Сходимость алгоритмов восстановления изображений со сглаживанием Гиббса». IEEE Транс. Мед. Изображение . 9 (4): 439–446. дои : 10.1109/42.61759 . ПМИД 18222791 .

[zhang-6] Jump up to: ^а ^б Чжан, Тонг (2004). Решение крупномасштабных задач линейного прогнозирования с использованием алгоритмов стохастического градиентного спуска . ИКМЛ.

[7] Фридман, Дж. Х. (2001). «Аппроксимация жадными функциями: машина повышения градиента» . Анналы статистики . 26 (5): 1189–1232. дои : 10.1214/aos/1013203451 . JSTOR 2699986 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]