Непереходные игральные кости

Набор игральных костей является интранзитивным (или нетранзитивным), если он содержит три игральные кости, A , B и C , со свойством, что A выбрасывает больше, чем B более чем в половине случаев, а B выбрасывает выше, чем C более чем в половине случаев. но это неправда, что А выбрасывает больше, чем С, более чем в половине случаев. Другими словами, набор игральных костей является нетранзитивным, если бинарное отношение ( $X$ выбрасывает большее число, чем $Y$ более чем в половине случаев) на его элементах не является транзитивным . Проще говоря, A обычно побеждает B , B обычно побеждает C , A не обычно побеждает C. но

Можно найти наборы игральных костей с еще более сильным свойством: для каждого кубика в наборе есть другой кубик, на котором более чем в половине случаев выпадает большее число, чем его. Отличие состоит в том, что вместо « А побеждает обычно не С » теперь написано « С обычно побеждает А ». Используя такой набор игральных костей, можно изобрести игры, в которых есть предвзятость, которую люди, не привыкшие к непереходным играм в кости, могут не ожидать (см. Пример ). ^[1]^[2]^[3]^[4]

Пример

Рассмотрим следующий набор игральных костей.

Кубик А имеет стороны 2, 2, 4, 4, 9, 9.
Кубик B имеет стороны 1, 1, 6, 6, 8, 8.
Кубик C имеет стороны 3, 3, 5, 5, 7, 7.

Вероятность того , что A выпадет большее число, чем B , вероятность того, что B выпадет больше, чем C , и вероятность того, что C выпадет больше, чем A, — все это ⁠ 5/9 поэтому ⁠ , этот набор игральных костей непереходен. На самом деле, у него есть еще более сильное свойство: для каждого кубика в наборе есть другой кубик, на котором более чем в половине случаев выпадает большее число, чем он.

Теперь рассмотрим следующую игру, в которой используются игральные кости.

Первый игрок выбирает кубик из набора.
Второй игрок выбирает один кубик из оставшихся.
Оба игрока бросают кубик; побеждает игрок, выпавший большее число.

Если в эту игру играют с переходным набором кубиков, она либо справедлива, либо предвзята в пользу первого игрока, поскольку первый игрок всегда может найти кубик, который не будет побит никакими другими кубиками более чем в половине случаев. Однако, если в нее играют с набором кубиков, описанным выше, игра смещается в пользу второго игрока, поскольку второй игрок всегда может найти кубик, который с вероятностью побьет кубик первого игрока. ⁠ 5 / 9 ⁠ . В следующих таблицах показаны все возможные исходы для всех трех пар игральных костей.

А С	2	4	9	Б А	1	6	8	С Б	3	5	7
Игрок 1 выбирает кубик А. Игрок 2 выбирает кубик C.				Игрок 1 выбирает кубик B. Игрок 2 выбирает кубик А.				Игрок 1 выбирает кубик C. Игрок 2 выбирает кубик B.
3	С	А	А	2	А	Б	Б	1	С	С	С
5	С	С	А	4	А	Б	Б	6	Б	Б	С
7	С	С	А	9	А	А	А	8	Б	Б	Б

Вариации

Кости Эфрона

Игральные кости Эфрона — это набор из четырех непереходных игральных костей, изобретенных Брэдли Эфроном . ^[5]

На шести гранях четырех кубиков A, B, C, D есть следующие числа:

А: 4, 4, 4, 4, 0, 0
Б: 3, 3, 3, 3, 3, 3
С: 6, 6, 2, 2, 2, 2
Д: 5, 5, 5, 1, 1, 1

Каждый кубик побивает предыдущий кубик в списке с закруглением с вероятностью ⁠ 2 / 3 ⁠ . C превосходит A с вероятностью ⁠ 5 / 9 ⁠ , а B и D имеют равные шансы победить другого. ^[5] Если у каждого игрока есть один набор кубиков Эфрона, существует континуум оптимальных стратегий для одного игрока, в котором они выбирают свои кости со следующими вероятностями, где 0 ≤ x ≤ ⁠ 3 / 7 ⁠ : ^[5]

P (выберите A) = x

P(выберите B) = ⁠ 1 2 ⁠ - ⁠ 5 6 ⁠ x

P (выберите C) = x

P(выберите D) = ⁠ 1 2 ⁠ - ⁠ 7 6 ⁠ x

Кости Мивина

Игральные кости Мивина были изобретены в 1975 году физиком Михаэлем Винкельманном.

Рассмотрим набор из трех игральных костей III, IV и V такой, что

Игральная кость III имеет стороны 1, 2, 5, 6, 7, 9.
Игральный кубик IV имеет стороны 1, 3, 4, 5, 8, 9.
Игральная кость V имеет стороны 2, 3, 4, 6, 7, 8.

Затем:

вероятность равна того, что III выпадет большее число, чем IV, ⁠ 17 / 36 ⁠
вероятность того, что IV выпадет большее число, чем V, равна ⁠ 17 / 36 ⁠
Вероятность того, что V выпадет большее число, чем III, равна ⁠ 17 / 36 ⁠

Уоррен Баффет

Уоррен Баффет известен как поклонник непереходных игральных костей. В книге « Формула удачи: нерассказанная история научной системы ставок, победившей казино и Уолл-стрит», дискуссия между ним и Эдвардом Торпом описана . Баффет и Торп обсудили общий интерес к непереходным игральным костям. «Это математическая диковина, разновидность «хитрых» игральных костей, которые сбивают с толку представления большинства людей о вероятности».

Баффет однажды попытался выиграть игру в кости с Биллом Гейтсом, используя непереходные игральные кости. «Баффет предложил каждому из них выбрать один из кубиков, а затем сбросить два других. Они делали ставку на то, кто чаще всего выкинет наибольшее число. Баффет предложил позволить Гейтсу первым выбрать свой кубик. Это предложение мгновенно вызвало любопытство Гейтса. Он попросил Баффета осмотреть кости, после чего потребовал, чтобы Баффет сделал выбор первым». ^[6]

В 2010 году журнал Wall Street Journal процитировал Шэрон Осберг, партнера Баффета по бриджу, заявившую, что, когда она впервые посетила его офис 20 лет назад, он обманом заставил ее сыграть в игру с непереходными игральными костями, в которой невозможно выиграть, и «посчитал это забавным». ^[7]

Непереходный набор кубиков для более чем двух игроков

Ряд людей представили варианты непереходных игральных костей, в которых можно соревноваться более чем с одним противником.

Три игрока

Оскар кости

Оскар ван Девентер представил набор из семи игральных костей (все грани с вероятностью ⁠ 1 / 6 ⁠ ) следующим образом: ^[8]

А: 2, 0 2, 14, 14, 17, 17
Б: 7, 0 7, 10, 10, 16, 16
С: 5, 0 5, 13, 13, 15, 15
Д: 3, 0 3, 0 9, 0 9, 21, 21
Э: 1, 0 1, 12, 12, 20, 20
Ф: 6, 0 6, 0 8, 0 8, 19, 19
Г: 4, 0 4, 11, 11, 18, 18

Можно проверить, что A превосходит {B,C,E}; B бьет {C,D,F}; C бьет {D,E,G}; D бьет {A,E,F}; E бьет {B,F,G}; F бьет {A,C,G}; G превосходит {A,B,D}. Следовательно, для произвольно выбранных двух кубиков найдется третий, который побьет оба. А именно,

G бьет {A, B}; F бьет {A, C}; G бьет {A, D}; D бьет {A,E}; D бьет {A, F}; F бьет {A,G};
A превосходит {B, C}; G бьет {B, D}; A превосходит {B,E}; E бьет {B, F}; E бьет {B,G};
B бьет {C,D}; A бьет {C,E}; B бьет {C,F}; F бьет {C,G};
C бьет {D,E}; B бьет {D,F}; C бьет {D,G};
D бьет {E, F}; C бьет {E,G};
E бьет {F,G}.

Что бы ни выбрали два противника, третий игрок найдет один из оставшихся кубиков, который превзойдет кубики обоих противников.

Кости грязи

Доктор Джеймс Грайм обнаружил следующий набор из пяти игральных костей: ^[9]^[10]

А: 2, 2, 2, 7, 7, 7
Б: 1, 1, 6, 6, 6, 6
С: 0, 5, 5, 5, 5, 5
Д: 4, 4, 4, 4, 4, 9
Э: 3, 3, 3, 3, 8, 8

Можно убедиться в этом, если в игру играют с одним набором кубиков Грайма:

Доля A Доля B Доля C Доля D Доля E Доля A (первая цепочка);
Доля A, доля C, доля E, доля B, доля D, доля A (вторая цепочка).

Однако, когда игра ведется с двумя такими сетами, то первая цепочка остается той же, за исключением того, что D бьет C, а вторая цепочка меняется на обратную (т. е. A бьет D бьет B бьет E бьет C бьет A). Следовательно, какие бы кубики ни выбрали два противника, третий игрок всегда может найти один из оставшихся кубиков, который побьет их обоих (при условии, что игроку тогда разрешено выбирать между вариантом с одним кубиком и вариантом с двумя кубиками):

Наборы выбраны оппонентами		Выигрышный набор кубиков
Наборы выбраны оппонентами		Тип	Число
А	Б	И	1
А	С	И	2
А	Д	С	2
А	И	Д	1
Б	С	А	1
Б	Д	А	2
Б	И	Д	2
С	Д	Б	1
С	И	Б	2
Д	И	С	1

Четыре игрока

Набор для четырех игроков пока не обнаружен, но доказано, что для такого набора потребуется не менее 19 кубиков. ^[9]^[11]

Непереходные четырехгранные игральные кости

Тетраэдры можно использовать как игральные кости с четырьмя возможными результатами .

Набор 1

А: 1, 4, 7, 7
Б: 2, 6, 6, 6
С: 3, 5, 5,8

Р(А > В) = Р(В > С) = Р(С > А) = ⁠ 9 / 16 ⁠

В следующих таблицах показаны все возможные результаты:

Б А	2	6	6	6
1	Б	Б	Б	Б
4	А	Б	Б	Б
7	А	А	А	А
7	А	А	А	А

В игре «А против Б» А выигрывает в 9 из 16 случаев.

С Б	3	5	5	8
2	С	С	С	С
6	Б	Б	Б	С
6	Б	Б	Б	С
6	Б	Б	Б	С

В игре «B против C» B выигрывает в 9 случаях из 16.

А С	1	4	7	7
3	С	А	А	А
5	С	С	А	А
5	С	С	А	А
8	С	С	С	С

В игре «С против А» С побеждает в 9 из 16 случаев.

Набор 2

А: 3, 3, 3, 6
Б: 2, 2, 5, 5
С: 1, 4, 4, 4

Р(А > В) = Р(В > С) = ⁠ 10/16 ⁠ 9/16 = , P(C > A)

Непереходные 12-гранные игральные кости

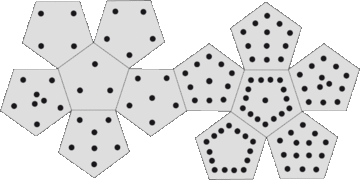
По аналогии с непереходными шестигранными игральными костями, существуют также додекаэдры, которые служат непереходными двенадцатигранными игральными костями . Сумма очков на каждом кубике равна 114. На каждом из додекаэдров нет повторяющихся чисел.

Додекаэдры Мивина (набор 1) циклически выигрывают друг у друга в соотношении 35:34.

Додекаэдры Мивина (набор 2) циклически выигрывают друг у друга в соотношении 71:67.

Набор 1:

Д III	фиолетовый	1	2			5	6	7		9	10	11			14	15	16		18
Д IV	красный	1		3	4	5			8	9	10		12	13	14			17	18
D V	темно-серый		2	3	4		6	7	8			11	12	13		15	16	17

Д III
Д IV
D V

Набор 2:

Д VI	голубой	1	2	3	4					9	10	11	12	13	14			17	18
Д VII	груша зеленая	1	2			5	6	7	8	9	10					15	16	17	18
Д VIII	светло-серый			3	4	5	6	7	8			11	12	13	14	15	16

Д VI
Д VII
Д VIII

Непереходные 12-гранные игральные кости с простыми числами

Также возможно построить наборы нетранзитивных додекаэдров, в которых нет повторяющихся чисел и все числа являются простыми. Непереходные додекаэдры Мивина с простыми числами циклически выигрывают друг у друга в соотношении 35:34.

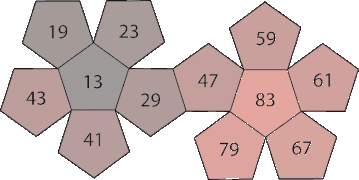
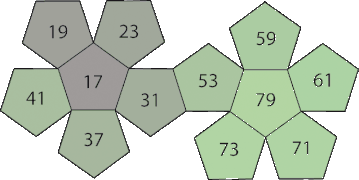
Набор 1: Сумма чисел равна 564.

ПД 11	от серого до синего	13	17	29	31	37	43	47	53	67	71	73	83
ПД 12	от серого до красного	13	19	23	29	41	43	47	59	61	67	79	83
ПД 13	от серого до зеленого	17	19	23	31	37	41	53	59	61	71	73	79

ПД 11
ПД 12
ПД 13

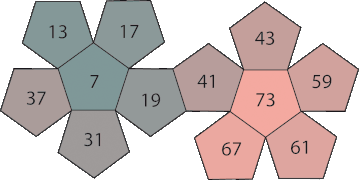
Набор 2: Сумма чисел равна 468.

ПД 1	от оливкового до синего	7	11	19	23	29	37	43	47	53	61	67	71
ПД 2	от бирюзового до красного	7	13	17	19	31	37	41	43	59	61	67	73
ПД 3	от фиолетового до зеленого	11	13	17	23	29	31	41	47	53	59	71	73

ПД 1
ПД 2
ПД 3

См. также

Ссылки

^ Вайсштейн, Эрик В. «Кости Эфрона» . Вольфрам Математический мир . Проверено 12 января 2021 г.
^ Богомольный, Александр . «Нетранзитивные игральные кости» . Разрежьте узел . Архивировано из оригинала 12 января 2016 г.
^ Сэвидж, Ричард П. (май 1994 г.). «Парадокс нетранзитивных игральных костей» . Американский математический ежемесячник . 101 (5): 429–436. дои : 10.2307/2974903 . JSTOR 2974903 .
^ Рамп, Кристофер М. (июнь 2001 г.). «Стратегии броска костей Эфрона» . Журнал «Математика» . 74 (3): 212–216. дои : 10.2307/2690722 . JSTOR 2690722 . Проверено 12 января 2021 г.
^ Jump up to: ^а ^б ^с Рамп, Кристофер М. (июнь 2001 г.). «Стратегии броска костей Эфрона» . Журнал «Математика» . 74 (3): 212–216. дои : 10.2307/2690722 . JSTOR 2690722 . Проверено 12 января 2021 г.
^ Билл Гейтс ; Джанет Лоу (14 октября 1998 г.). Выступление Билла Гейтса: мнение величайшего предпринимателя мира . Нью-Йорк: Уайли. ISBN 9780471293538 . Проверено 29 ноября 2011 г.
^ «Как брак, только более прочный» . Yahoo! Финансы . Уолл Стрит Джорнал . 06.12.2010. Архивировано из оригинала 10 декабря 2010 г. Проверено 29 ноября 2011 г.
^ Пегг, Эд младший (11 июля 2005 г.). «Турнирные кости» . Математические игры . Математическая ассоциация Америки . Архивировано из оригинала 4 августа 2005 г. Проверено 6 июля 2012 г.
^ Jump up to: ^а ^б Грайм, Джеймс. «Нетранзитивные игральные кости» . Архивировано из оригинала 14 мая 2016 г.
^ Пасчуто, Николас (2016). «Тайна нетранзитивной грайм-игры» . Обзор бакалавриата . 12 (1): 107–115 – через Государственный университет Бриджуотера.
^ Рид, Кеннет; Макрей, А.А.; Хедетниеми, С.М.; Хедетниеми, Стивен (1 января 2004 г.). «Доминирование и неизбыточность в турнирах» . Австралазийский журнал комбинаторики [только в электронном виде] . 29 .

Источники

Гарднер, Мартин (2001). Колоссальная книга по математике: классические головоломки, парадоксы и проблемы: теория чисел, алгебра, геометрия, вероятность, топология, теория игр, бесконечность и другие темы развлекательной математики (1-е изд.). Нью-Йорк: WW Norton & Company. п. 286 –311. ^{[ ISBN отсутствует ]}
Игровая математика с кубиками Мивина (на немецком языке). Лембергер образовательное издательство. ISBN 978-3-85221-531-0 .

Внешние ссылки

[MathWorld-1] Вайсштейн, Эрик В. «Кости Эфрона» . Вольфрам Математический мир . Проверено 12 января 2021 г.

[2] Богомольный, Александр . «Нетранзитивные игральные кости» . Разрежьте узел . Архивировано из оригинала 12 января 2016 г.

[3] Сэвидж, Ричард П. (май 1994 г.). «Парадокс нетранзитивных игральных костей» . Американский математический ежемесячник . 101 (5): 429–436. дои : 10.2307/2974903 . JSTOR 2974903 .

[4] Рамп, Кристофер М. (июнь 2001 г.). «Стратегии броска костей Эфрона» . Журнал «Математика» . 74 (3): 212–216. дои : 10.2307/2690722 . JSTOR 2690722 . Проверено 12 января 2021 г.

[efron-5] Jump up to: ^а ^б ^с Рамп, Кристофер М. (июнь 2001 г.). «Стратегии броска костей Эфрона» . Журнал «Математика» . 74 (3): 212–216. дои : 10.2307/2690722 . JSTOR 2690722 . Проверено 12 января 2021 г.

[6] Билл Гейтс ; Джанет Лоу (14 октября 1998 г.). Выступление Билла Гейтса: мнение величайшего предпринимателя мира . Нью-Йорк: Уайли. ISBN 9780471293538 . Проверено 29 ноября 2011 г.

[7] «Как брак, только более прочный» . Yahoo! Финансы . Уолл Стрит Джорнал . 06.12.2010. Архивировано из оригинала 10 декабря 2010 г. Проверено 29 ноября 2011 г.

[8] Пегг, Эд младший (11 июля 2005 г.). «Турнирные кости» . Математические игры . Математическая ассоциация Америки . Архивировано из оригинала 4 августа 2005 г. Проверено 6 июля 2012 г.

[A-9] Jump up to: ^а ^б Грайм, Джеймс. «Нетранзитивные игральные кости» . Архивировано из оригинала 14 мая 2016 г.

[10] Пасчуто, Николас (2016). «Тайна нетранзитивной грайм-игры» . Обзор бакалавриата . 12 (1): 107–115 – через Государственный университет Бриджуотера.

[11] Рид, Кеннет; Макрей, А.А.; Хедетниеми, С.М.; Хедетниеми, Стивен (1 января 2004 г.). «Доминирование и неизбыточность в турнирах» . Австралазийский журнал комбинаторики [только в электронном виде] . 29 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]