Теорема Миллера

Теорема Миллера относится к процессу создания эквивалентных схем . Он утверждает, что элемент с плавающим сопротивлением, питаемый от двух источников напряжения, соединенных последовательно, может быть разделен на два заземленных элемента с соответствующими импедансами. Существует также двойственная теорема Миллера относительно импеданса, создаваемого двумя источниками тока, соединенными параллельно. Обе версии основаны на двух законах цепи Кирхгофа .

Теоремы Миллера — это не только чисто математические выражения. Эти механизмы объясняют важные явления в схемах, связанные с изменением импеданса ( эффект Миллера , виртуальное заземление , начальная загрузка , отрицательное сопротивление и т. д.) и помогают в проектировании и понимании различных распространенных схем (усилители с обратной связью, резистивные и зависящие от времени преобразователи, преобразователи с отрицательным импедансом и т. д.). ). Теоремы полезны при «анализе схем», особенно при анализе схем с обратной связью. ^[1] и некоторые транзисторные усилители высоких частот. ^[2]

Между теоремой Миллера и эффектом Миллера существует тесная связь: теорему можно рассматривать как обобщение эффекта, а эффект можно рассматривать как частный случай теоремы.

Теорема Миллера (для напряжений)

Определение

Теорема Миллера устанавливает, что в линейной цепи, если существует ветвь с сопротивлением $Z$ , соединяющий два узла с узловыми напряжениями $V_{1}$ и $V_{2}$ , мы можем заменить эту ветвь двумя ветвями, соединяющими соответствующие узлы с землей сопротивлениями соответственно ${\frac {Z}{1-K}}$ и ${\frac {KZ}{K-1}}$ , где $K={\frac {V_{2}}{V_{1}}}$ . Теорему Миллера можно доказать, используя эквивалентную технику двухпортовой сети для замены двухпортовой сети ее эквивалентом и применяя теорему о поглощении источника. ^[3] Эта версия теоремы Миллера основана на законе напряжения Кирхгофа ; по этой причине ее также называют теоремой Миллера для напряжений .

Объяснение

Теорема Миллера подразумевает, что элемент импеданса питается от двух произвольных (не обязательно зависимых) источников напряжения, соединенных последовательно через общую землю. На практике один из них выступает в роли основного (независимого) источника напряжения с напряжением $V_{1}$ а другой – как дополнительный (линейно зависимый) источник напряжения с напряжением $V_{2}=K{V_{1}}$ . Идея теоремы Миллера (изменение импеданса цепи, видимой со стороны входного и выходного источников) раскрывается ниже путем сравнения двух ситуаций – без и с подключением дополнительного источника напряжения. $V_{2}$ .

Если $V_{2}$ были равны нулю (не было второго источника напряжения или правого конца элемента с сопротивлением $Z$ был только что заземлен), входной ток, протекающий через элемент, будет определяться, согласно закону Ома, только величиной $V_{1}$

I_{in0}={\frac {V_{1}}{Z}}

а входное сопротивление цепи будет

Z_{in0}={\frac {V_{1}}{I_{in0}}}=Z.

Поскольку включен второй источник напряжения, входной ток зависит от обоих напряжений. По своей полярности, $V_{2}$ вычитается из или добавляется к $V_{1}$ ; итак, входной ток уменьшается/увеличивается

I_{in}={\frac {V_{1}-V_{2}}{Z}}={\frac {(1-K)}{Z}}{V_{1}}={(1-K)}{I_{in0}}

и входное сопротивление цепи, если смотреть со стороны источника входного сигнала, соответственно увеличивается/уменьшается

Z_{in}={\frac {V_{1}}{I_{in}}}={\frac {Z}{1-K}}.

Итак, теорема Миллера выражает тот факт, что подключение второго источника напряжения с пропорциональным напряжением $V_{2}=K{V_{1}}$ последовательно с источником входного напряжения изменяются действующее напряжение, ток и соответственно полное сопротивление цепи, видимое со стороны источника входного напряжения . В зависимости от полярности, $V_{2}$ действует как дополнительный источник напряжения, помогая или противодействуя основному источнику напряжения, пропуская ток через полное сопротивление.

Кроме того, представляя комбинацию двух источников напряжения как новый составной источник напряжения, теорему можно объяснить путем объединения реального элемента и второго источника напряжения в новый виртуальный элемент с динамически изменяемым импедансом . С этой точки зрения, $V_{2}$ дополнительное напряжение, которое искусственно увеличивает/уменьшает падение напряжения $V_{z}$ поперек импеданса $Z$ тем самым уменьшая/увеличивая ток. Пропорция между напряжениями определяет значение полученного импеданса (см. таблицы ниже) и дает в общей сложности шесть групп типовых применений .

**Вычитание $V_{2}$ от $V_{1}$**
$V_{2}$ против $V_{1}$	$V_{2}=0$	$0<V_{2}<V_{1}$	$V_{2}=V_{1}$	$V_{2}>V_{1}$
Импеданс	нормальный	повысился	бесконечный	отрицательный с инверсией тока

**Добавление $V_{2}$ к $V_{1}$**
$V_{2}$ против $V_{z}$	$V_{2}=0$	$0<V_{2}<V_{z}$	$V_{2}=V_{z}$	$V_{2}>V_{z}$
Импеданс	нормальный	уменьшился	ноль	отрицательный с инверсией напряжения

Сопротивление цепи, если смотреть со стороны выходного источника, можно определить аналогично, если напряжения $V_{1}$ и $V_{2}$ меняются местами и коэффициент $K$ заменяется на ${\frac {1}{K}}$

Z_{in2}={\frac {{K}{Z}}{K-1}}.

Выполнение

Типичная реализация теоремы Миллера на основе несимметричного усилителя напряжения.

Чаще всего теорему Миллера можно наблюдать и реализовать с помощью устройства, состоящего из элемента с импедансом $Z$ подключается между двумя клеммами заземленной общей линейной сети. ^[2] Обычно усилитель напряжения с коэффициентом усиления $A_{V}=K$ Такой линейной сетью служит, но эту роль могут выполнять и другие устройства: человек и потенциометр в потенциометрическом измерителе нулевого баланса , электромеханический интегратор (сервомеханизмы с использованием потенциометрических датчиков обратной связи) и т. д.

В реализации усилителя входное напряжение $V_{i}$ служит как $V_{1}$ и выходное напряжение $V_{o}$ как $V_{2}$ . Во многих случаях источник входного напряжения имеет некоторый внутренний импеданс. $Z_{int}$ или подключено дополнительное входное сопротивление, которое в сочетании с $Z$ , представляет обратную связь. В зависимости от типа усилителя (неинвертирующий, инвертирующий или дифференциальный) обратная связь может быть положительной, отрицательной или смешанной.

Устройство усилителя Миллера имеет два аспекта:

усилитель можно рассматривать как дополнительный источник напряжения, преобразующий фактический импеданс в виртуальный импеданс (усилитель изменяет импеданс реального элемента)
виртуальный импеданс можно рассматривать как элемент, подключенный параллельно входу усилителя (виртуальный импеданс изменяет входное сопротивление усилителя).

Приложения

Введение импеданса, соединяющего входные и выходные порты усилителя, добавляет сложность процесса анализа. Теорема Миллера помогает уменьшить сложность в некоторых схемах, особенно с обратной связью ^[2] путем преобразования их в более простые эквивалентные схемы. Но теорема Миллера — не только эффективный инструмент для создания эквивалентных схем; это также мощный инструмент для проектирования и понимания схем, основанных на изменении импеданса с помощью дополнительного напряжения . В зависимости от полярности выходного напряжения по отношению к входному и соотношения между их величинами выделяют шесть групп типовых ситуаций. В некоторых из них феномен Миллера проявляется как желательные ( бутстрэппинг ) или нежелательные ( эффект Миллера ) непреднамеренные эффекты; в других случаях оно вводится намеренно.

Приложения, основанные на вычитании V ₂ из V ₁

В этих приложениях выходное напряжение $V_{o}$ вставлен с противоположной полярностью по отношению к входному напряжению $V_{i}$ путешествуя по контуру (но относительно земли полярность та же). В результате эффективное напряжение и ток через полное сопротивление уменьшаются; входное сопротивление увеличивается.

Повышенное сопротивление реализовано неинвертирующим усилителем с коэффициентом усиления $0<A_{v}<1$ . Выходное напряжение (величина) меньше входного напряжения. $V_{i}$ и частично нейтрализует его. Примерами являются несовершенные повторители напряжения ( эмиттер , исток , катодный повторитель и т. д.) и усилители с последовательной отрицательной обратной связью ( эмиттерная дегенерация ), входное сопротивление которых умеренно увеличено.

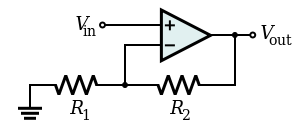
Бесконечный импеданс использует неинвертирующий усилитель с $A_{v}=1$ . Выходное напряжение равно входному напряжению $V_{i}$ и полностью нейтрализует его. Примерами являются потенциометрические измерители нулевого баланса , повторители на операционных усилителях и усилители с последовательной отрицательной обратной связью ( повторитель на операционном усилителе и неинвертирующий усилитель ), в которых входное сопротивление схемы значительно увеличивается. Этот метод называется начальной загрузкой и намеренно используется в схемах смещения, схемах защиты входа, ^[4] и т. д.

Отрицательное сопротивление, полученное путем инверсии тока, реализуется неинвертирующим усилителем с $A_{v}>1$ . Ток меняет свое направление, так как выходное напряжение выше входного. Если источник входного напряжения имеет некоторый внутренний импеданс $Z_{int}$ или если он подключен через другой импедансный элемент, то появляется положительная обратная связь. Типичным применением является преобразователь отрицательного сопротивления с инверсией тока (INIC), использующий как отрицательную, так и положительную обратную связь (отрицательная обратная связь используется для реализации неинвертирующего усилителя, а положительная обратная связь – для изменения импеданса).

Приложения, основанные на добавлении V ₂ к V ₁

В этих приложениях выходное напряжение $V_{o}$ вставляется с той же полярностью относительно входного напряжения $V_{i}$ путешествуя по контуру (но относительно земли полярность противоположна). В результате эффективное напряжение поперек и ток через сопротивление увеличиваются; входное сопротивление уменьшается.

Пониженное сопротивление реализуется инвертирующим усилителем, имеющим умеренный коэффициент усиления, обычно $10<A_{v}<1000$ . Это можно наблюдать как нежелательный эффект Миллера в каскадах усиления с общим эмиттером , общим истоком и общим катодом , где эффективная входная емкость увеличивается. Частотная компенсация для операционных усилителей общего назначения и транзисторных интеграторов Миллера являются примерами полезного использования эффекта Миллера.

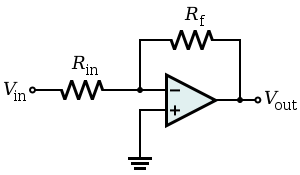
При нулевом импедансе используется инвертирующий усилитель (обычно операционный усилитель) с чрезвычайно высоким коэффициентом усиления. $A_{v}\to \infty$ . Выходное напряжение практически равно падению напряжения. $V_{z}$ через полное сопротивление и полностью нейтрализует его. Схема ведет себя как короткое замыкание и виртуальная земля на входе появляется ; поэтому он не должен приводиться в действие источником постоянного напряжения. Для этого некоторые схемы управляются источником постоянного тока или источником реального напряжения с внутренним сопротивлением: преобразователем ток-напряжение (трансимпедансный усилитель), емкостным интегратором (называемым также интегратором тока или усилителем заряда ), сопротивлением- преобразователь напряжения (резистивный датчик, подключаемый вместо импедансного $Z$ ).

Остальные имеют дополнительное сопротивление, включенное последовательно ко входу: преобразователь напряжения в ток (усилитель крутизны), инвертирующий усилитель , суммирующий усилитель , индуктивный интегратор, емкостной дифференциатор, резистивно-емкостный интегратор , емкостно-резистивный дифференциатор , индуктивно-резистивный дифференциатор и т. д. Инвертирующие интеграторы из этого списка являются примерами полезных и желательных применений эффекта Миллера в его крайнем проявлении.

Во всех этих инвертирующих схемах ОУ с параллельной отрицательной обратной связью входной ток увеличивается до максимального значения. Оно определяется только входным напряжением и входным сопротивлением по закону Ома ; это не зависит от сопротивления $Z$ .

Отрицательное сопротивление с инверсией напряжения реализуется путем применения как отрицательной, так и положительной обратной связи к операционному усилителю с дифференциальным входом. Источник входного напряжения должен иметь внутренний импеданс. $Z_{int}>0$ или его необходимо подключить через другой импедансный элемент ко входу. В этих условиях входное напряжение $V_{i}$ цепи меняет свою полярность, когда выходное напряжение превышает падение напряжения $V_{z}$ по сопротивлению ( $V_{i}=V_{z}-V_{o}<0$ ).

Типичным применением является преобразователь отрицательного импеданса с инверсией напряжения (VNIC). ^[5] Интересно, что входное напряжение схемы имеет ту же полярность, что и выходное, хотя оно подается на вход инвертирующего ОУ; источник входного сигнала имеет противоположную полярность как входному, так и выходному напряжениям схемы.

Обобщение схемы Миллера

Оригинальный эффект Миллера реализуется за счет емкостного сопротивления, подключенного между двумя узлами. Теорема Миллера обобщает эффект Миллера, поскольку предполагает произвольный импеданс. $Z$ соединен между узлами. Предполагается также постоянный коэффициент $K$ ; выражения тогда приведенные выше справедливы. Но модифицирующие свойства теоремы Миллера существуют даже тогда, когда эти требования нарушаются, и эту схему можно дополнительно обобщить путем динамизации импеданса и коэффициента.

Нелинейный элемент. Помимо импеданса, устройство Миллера может изменять ВАХ произвольного элемента. Схема диодного логарифмического преобразователя является примером нелинейного, практически обнулённого сопротивления , где логарифмическая прямая ВАХ диода преобразуется в вертикальную прямую линию, перекрывающую $y$ ось.

Не постоянный коэффициент. Если коэффициент $K$ варьируется, можно получить некоторые экзотические виртуальные элементы. Схема гиратора является примером такого виртуального элемента, в котором сопротивление $R_{L}$ модифицируется таким образом, чтобы имитировать индуктивность, емкость или обратное сопротивление.

Двойная теорема Миллера (для токов)

Определение

Существует также двойственная версия теоремы Миллера, основанная на законе тока Кирхгофа ( теорема Миллера для токов ): если в цепи есть ветвь с импедансом $Z$ соединение узла, где два тока $I_{1}$ и $I_{2}$ сходятся к земле, мы можем заменить эту ветвь двумя, проводящими упомянутые токи, с сопротивлениями соответственно равными $(1+\alpha )Z$ и ${\frac {(1+\alpha )Z}{\alpha }}$ , где $\alpha ={\frac {I_{2}}{I_{1}}}$ . Двойственная теорема может быть доказана путем замены двухпортовой сети ее эквивалентом и применения теоремы об поглощении источника. ^[3]

Объяснение

Двойная теорема Миллера на самом деле выражает тот факт, что подключение второго источника тока, производящего пропорциональный ток $I_{2}=KI_{1}$ параллельно с основным входным источником и импедансным элементом изменяется ток, протекающий через него, напряжение и соответственно полное сопротивление цепи, видимое со стороны входного источника. В зависимости от направления, $I_{2}$ действует как дополнительный источник тока, помогая или противодействуя основному источнику тока. $I_{1}$ для создания напряжения на импедансе. Комбинацию реального элемента и второго источника тока можно рассматривать как новый виртуальный элемент с динамически изменяемым импедансом.

Выполнение

Двойная теорема Миллера обычно реализуется с помощью устройства, состоящего из двух источников напряжения, питающих заземленное сопротивление. $Z$ через плавающие импедансы (см. рис. 3 ). Комбинации источников напряжения и соответствующих импедансов образуют два источника тока – основной и вспомогательный. Как и в случае с основной теоремой Миллера, второе напряжение обычно создается усилителем напряжения. В зависимости от типа усилителя (инвертирующий, неинвертирующий или дифференциальный) и коэффициента усиления входное сопротивление схемы может быть практически увеличенным, бесконечным, уменьшенным, нулевым или отрицательным.

Приложения

Как основная теорема Миллера, двойная версия не только помогает в процессе анализа цепей, но и является мощным инструментом для проектирования и понимания схем, основанных на изменении импеданса дополнительным током. Типичными применениями являются некоторые экзотические схемы с отрицательным импедансом в качестве компенсаторов нагрузки. ^[6] емкостные нейтрализаторы, ^[7] Источник тока Howland и его производный интегратор Deboo. ^[8] В последнем примере (см. там рис. 1) источник тока Хауланда состоит из источника входного напряжения $V_{in}$ , положительный резистор $R$ , нагрузка (конденсатор $C$ действует как импеданс $Z$ ) и преобразователь отрицательного импеданса INIC ( $R_{1}=R_{2}=R_{3}=R$ и операционный усилитель). Источник входного напряжения и резистор $R$ представляют собой несовершенный источник тока, пропускающий ток $I_{R}$ через нагрузку (см. рис. 3 в источнике). INIC действует как второй источник тока, пропуская «вспомогательный» ток. $I_{-R}$ через нагрузку. В результате общий ток, протекающий через нагрузку, остается постоянным, а сопротивление цепи, воспринимаемое источником входного сигнала, увеличивается. Для сравнения: в компенсаторе нагрузки ^{[ постоянная мертвая ссылка ]}, INIC пропускает весь необходимый ток через нагрузку; полное сопротивление цепи, наблюдаемое со стороны входного источника (сопротивление нагрузки), практически бесконечно.

Список конкретных приложений, основанных на теоремах Миллера

Ниже приведен список схемных решений, явлений и методов, основанных на двух теоремах Миллера.

Схемотехнические решения

Схемные явления и приемы

См. также

Ссылки

^ «Разные сетевые теоремы» . Netlecturer.com. Архивировано из оригинала 21 марта 2012 г. Проверено 3 февраля 2013 г.
^ Jump up to: ^а ^б ^с «EEE 194RF: Теорема Миллера» (PDF) . Проверено 3 февраля 2013 г.
^ Jump up to: ^а ^б «Теорема Миллера» . Paginas.fe.up.pt . Проверено 3 февраля 2013 г.
^ Работа с операционными усилителями с высоким импедансом. Архивировано 23 сентября 2010 г. на Wayback Machine AN-241.
^ «Анализ нелинейных цепей. Введение» (PDF) . Проверено 3 февраля 2013 г.
^ Компенсатор нагрузки с отрицательным сопротивлением помогает управлять тяжелыми нагрузками.
^ Д. Х. Шейнгольд (1964-01-01), «Преобразования импеданса и проводимости с использованием операционных усилителей» , The Lightning Empiricist , 12 (1) , получено 22 июня 2014 г.
^ «Рассмотрим интегратор единого источника питания «Deboo» . Максим-ic.com. 29 августа 2002 г. Проверено 3 февраля 2013 г.

Дальнейшее чтение

Основы микроэлектроники Бехзада Разави
Микроэлектронные схемы Аделя Седра и Кеннета Смита
Основы проектирования радиочастотных схем Джереми Эверард

Внешние ссылки

[1] «Разные сетевые теоремы» . Netlecturer.com. Архивировано из оригинала 21 марта 2012 г. Проверено 3 февраля 2013 г.

[sandiego-2] Jump up to: ^а ^б ^с «EEE 194RF: Теорема Миллера» (PDF) . Проверено 3 февраля 2013 г.

[paginas-3] Jump up to: ^а ^б «Теорема Миллера» . Paginas.fe.up.pt . Проверено 3 февраля 2013 г.

[4] Работа с операционными усилителями с высоким импедансом. Архивировано 23 сентября 2010 г. на Wayback Machine AN-241.

[5] «Анализ нелинейных цепей. Введение» (PDF) . Проверено 3 февраля 2013 г.

[load_canceller-6] Компенсатор нагрузки с отрицательным сопротивлением помогает управлять тяжелыми нагрузками.

[7] Д. Х. Шейнгольд (1964-01-01), «Преобразования импеданса и проводимости с использованием операционных усилителей» , The Lightning Empiricist , 12 (1) , получено 22 июня 2014 г.

[8] «Рассмотрим интегратор единого источника питания «Deboo» . Максим-ic.com. 29 августа 2002 г. Проверено 3 февраля 2013 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]