Эквивалентный радиус антенны

Эквивалентный радиус проводника антенны определяется как:

$r_{e}=\exp \left\{{1 \over L^{2}}\oint _{\ell }\oint _{\ell }\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert \;dx\;dy\right\}$

где $\scriptstyle \ell$ проводника обозначает окружность , $\scriptstyle {L}$ длина окружности, $\scriptstyle {\boldsymbol {x}}$ и $\scriptstyle {\boldsymbol {y}}$ являются векторами, определяющими точки вдоль окружности, а $\scriptstyle {dx}$ и $\scriptstyle {dy}$ являются отрезками дифференциала вдоль него. Эквивалентный радиус позволяет использовать аналитические формулы или расчетные или экспериментальные данные , полученные для антенн, построенных из небольших проводников с однородным круглым поперечным сечением, которые можно применять при анализе антенн, построенных из небольших проводников с однородным, некруглым поперечным сечением. Здесь «маленький» означает, что наибольший размер поперечного сечения намного меньше длины волны. $\scriptstyle {\lambda }$.

Формулы

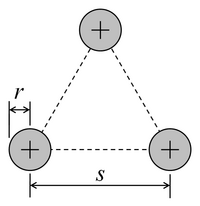
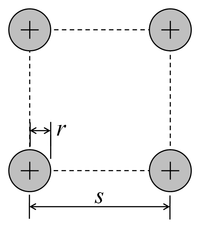
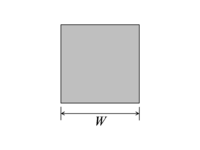
В следующей таблице приведены эквивалентные радиусы для различных поперечных сечений проводников, полученные из предположения, что 1) все размеры намного меньше $\scriptstyle {\lambda }$, 2) для поперечных сечений, состоящих из нескольких проводников, расстояния между проводниками намного больше, чем любой размер отдельного проводника. . Формулы для квадратных и треугольных сечений следуют из численного вычисления двойного интеграла. Все остальные формулы точны.

Поперечное сечение	Описание	Эквивалентный радиус
	Два одинаковых круглых проводника	${\sqrt {rs}}$
	Два круглых проводника с неравными радиусами	$\exp \left\{{r_{1}^{2}\ln r_{1}+r_{2}^{2}\ln r_{2}+2r_{1}r_{2}\ln S \over (r_{1}+r_{2})^{2}}\right\}$
	Идентичные круглые проводники расположен в треугольнике	$\left(rs^{2}\right)^{1/3}$
	Идентичные круглые проводники расположен в квадрате	$\left({\sqrt {2}}\,rs^{3}\right)^{1/4}$
	Идентичные круглые проводники расположен в пятиугольнике	$\left(2.62\,rs^{4}\right)^{1/5}$
	Идентичные круглые проводники расположен в шестиугольнике	$\left(6\,rs^{5}\right)^{1/6}$
	$N$ Идентичные круглые проводники равномерно распределены по кругу	$\left(NrR^{N-1}\right)^{1/N}$
	Плоский, бесконечно тонкий проводник.	$\displaystyle {We^{-3/2}\approx 0.22\,W}$
	Квадратный проводник	$\displaystyle {0.58\,W}$
	Равносторонний треугольный проводник	$\displaystyle {0.41\,W}$

Вывод

Эквивалентный радиус получается путем приравнивания среднего векторного магнитного потенциала на поверхности проводника произвольного сечения потенциалу на поверхности цилиндра.

Предположим, что размеры поперечного сечения проводника малы по сравнению с длиной волны, ток течет только в осевом направлении вдоль проводника, распределение тока медленно меняется по длине проводника и ток примерно равномерно распределяется по его окружности (из-за скин-эффекта ). Более того, только ток в окрестности любой точки проводника вносит значительный вклад в потенциал в этой точке. Зависимость от времени игнорируется, поскольку ее можно учесть путем умножения распределения тока на изменяющуюся во времени синусоиду. Эти условия подразумевают, что существует квазистатическое состояние и что геометрия, по сути, представляет собой бесконечно длинный проводник с постоянной плотностью поверхностного тока. $\scriptstyle {Q}$ (ток на площадь), тем самым сводя трехмерную задачу к двумерной. Также подразумевается, что векторный магнитный потенциал параллелен оси проводника.

Сначала рассмотрим потенциал в фиксированной точке $\scriptstyle {\boldsymbol {y}}$ на окружности произвольного сечения. С окружностью, разделенной на дифференциальные сегменты $\scriptstyle {dx}$, распределение тока можно аппроксимировать, поместив вертикальный линейный ток внутри каждого сегмента, каждый с линейной плотностью $\scriptstyle {Q\,dx}$ (ток по длине). Хорошо известно, что потенциал такого линейного тока равен $\scriptstyle {-(\mu _{0}Qdx/2\pi )\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert }$, где $\scriptstyle {\mu _{0}}$ – константа проницаемости. Потенциал в $\scriptstyle {\boldsymbol {y}}$ представляет собой сумму потенциалов всех полосок, которая равна

$A({\boldsymbol {y}})=-{\mu _{0}Q \over 2\pi }\oint _{\ell }\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert \;dx.$

Тогда средний потенциал

${\bar {A}}={1 \over L}\oint _{\ell }A({\boldsymbol {y}})\;dy\,=-{\mu _{0}Q \over 2\pi L}\oint _{\ell }\oint _{\ell }\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert \;dx\;dy.$

Теперь рассмотрим случай цилиндра с той же линейной плотностью тока, что и проводник произвольного сечения. Хорошо известно также, что потенциал в любой точке его поверхности, равный также ее среднему потенциалу, равен

$A_{c}=-{\mu _{0}QL \over 2\pi }\ln \left(r_{e}\right).$

Приравнивание $\scriptstyle {\bar {A}}$ и $\scriptstyle {A_{c}}$ урожайность

$\ln \left(r_{e}\right)={1 \over L^{2}}\oint _{\ell }\oint _{\ell }\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert \;dx\;dy.$

Возведение обеих сторон в степень приводит к формуле эквивалентного радиуса.

Формула эквивалентного радиуса дает последовательные результаты. Если размеры поперечного сечения проводника масштабировать в коэффициент $\scriptstyle {\alpha }$эквивалентный радиус масштабируется как $\scriptstyle {|\alpha |}$. Также эквивалентный радиус цилиндрического проводника равен радиусу проводника.