Схема бабочки

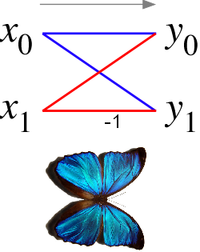
График потока сигналов, соединяющий входы x (слева) с выходами y , которые зависят от них (справа), для шага «бабочка» БПФ Кули – Тьюки по основанию 2. Эта диаграмма напоминает бабочку (как на показанной для сравнения морфо-бабочке ), отсюда и название, хотя в некоторых странах ее еще называют диаграммой песочных часов.

В контексте быстрого преобразования Фурье алгоритмов « бабочка» — это часть вычислений, которая объединяет результаты меньших дискретных преобразований Фурье (ДПФ) в большее ДПФ или наоборот (разбивая большее ДПФ на подпреобразования). Название «бабочка» происходит от формы диаграммы потока данных в случае счисления 2, как описано ниже. ^[1] Считается, что самое раннее появление этого термина в печати произошло в техническом отчете Массачусетского технологического института за 1969 год . ^[2]^[3] Эту же структуру можно найти и в алгоритме Витерби , используемом для поиска наиболее вероятной последовательности скрытых состояний.

Чаще всего термин «бабочка» появляется в контексте алгоритма БПФ Кули-Тьюки , который рекурсивно разбивает ДПФ составного размера n = rm на r меньших преобразований размера m, где r — «основание» преобразования. Эти меньшие ДПФ затем объединяются с помощью бабочек размера r , которые сами представляют собой ДПФ размера r (выполняемые m раз на соответствующих выходных данных подпреобразований), предварительно умноженные на корни из единицы (известные как коэффициенты поворота ). (Это случай «децимации по времени»; можно также выполнить шаги в обратном порядке, известные как «децимация по частоте», когда бабочки появляются первыми, а затем умножаются на коэффициенты вращения. См. также Кули-Тьюки о БПФ статью .)

бабочки Radix Диаграмма - 2

В случае алгоритма Кули-Тьюки счисления 2 бабочка представляет собой просто ДПФ размера 2, который принимает два входных параметра ( x ₀ , x ₁ ) (соответствующие выходные данные двух субпреобразований) и дает два выходных сигнала ( y ₀ , y ₁ ) по формуле (без учета коэффициентов вращения ):

y_{0}=x_{0}+x_{1}\,

y_{1}=x_{0}-x_{1}.\,

Если нарисовать диаграмму потока данных для этой пары операций, то линии от ( x ₀ , x ₁ ) до ( y ₀ , y ₁ ) пересекаются и напоминают крылья бабочки , отсюда и название (см. также иллюстрацию справа). ).

БПФ с прореживанием во времени по основанию 2 разбивает ДПФ длины N на два ДПФ длины N /2, после чего следует этап объединения, состоящий из множества операций типа «бабочка».

Более конкретно, алгоритм БПФ с прореживанием во времени по основанию 2 при n = 2. ^п входные данные относительно примитивного корня n-й степени из единицы $\omega _{n}^{k}=e^{-{\frac {2\pi ik}{n}}}$ опирается на O( n log ₂ n ) бабочек вида:

y_{0}=x_{0}+x_{1}\omega _{n}^{k}\,

y_{1}=x_{0}-x_{1}\omega _{n}^{k},\,

где k — целое число, зависящее от вычисляемой части преобразования. Тогда как соответствующее обратное преобразование математически можно выполнить, заменив ω на ω ⁻¹ (и, возможно, умножив на общий масштабный коэффициент, в зависимости от соглашения о нормализации), можно также напрямую инвертировать бабочек:

x_{0}={\frac {1}{2}}(y_{0}+y_{1})\,

x_{1}={\frac {\omega _{n}^{-k}}{2}}(y_{0}-y_{1}),\,

соответствующий алгоритму БПФ с прореживанием по частоте.

Другое использование [ править ]

Бабочку также можно использовать для улучшения случайности больших массивов частично случайных чисел, приводя каждое 32- или 64-битное слово в причинный контакт с каждым другим словом с помощью желаемого алгоритма хеширования, так что изменение любого одного бита имеет возможность изменения всех битов в большом массиве. ^[4]

См. также [ править ]

Ссылки [ править ]

^ Алан В. Оппенгейм, Рональд В. Шафер и Джон Р. Бак, Обработка сигналов в дискретном времени , 2-е издание (Аппер-Сэддл-Ривер, Нью-Джерси: Прентис-Холл, 1989)
^ Си Джей Вайнштейн (21 ноября 1969 г.). Эффекты квантования в цифровых фильтрах (отчет). Лаборатория Линкольна Массачусетского технологического института . п. 42. Архивировано из оригинала 11 февраля 2015 года . Проверено 10 февраля 2015 г. Это вычисление, называемое «бабочкой».
^ Ципра, Барри А. (4 июня 2012 г.). «БПФ и диаграмма-бабочка» . mathoverflow.net . Проверено 10 февраля 2015 г.
^ * Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 7.2. Полное хеширование большого массива» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8 , заархивировано из оригинала 11 августа 2011 г. , получено 13 августа 2011 г.

Внешние ссылки [ править ]

[Oppenheim89-1] Алан В. Оппенгейм, Рональд В. Шафер и Джон Р. Бак, Обработка сигналов в дискретном времени , 2-е издание (Аппер-Сэддл-Ривер, Нью-Джерси: Прентис-Холл, 1989)

[2] Си Джей Вайнштейн (21 ноября 1969 г.). Эффекты квантования в цифровых фильтрах (отчет). Лаборатория Линкольна Массачусетского технологического института . п. 42. Архивировано из оригинала 11 февраля 2015 года . Проверено 10 февраля 2015 г. Это вычисление, называемое «бабочкой».

[3] Ципра, Барри А. (4 июня 2012 г.). «БПФ и диаграмма-бабочка» . mathoverflow.net . Проверено 10 февраля 2015 г.

[4] * Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 7.2. Полное хеширование большого массива» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8 , заархивировано из оригинала 11 августа 2011 г. , получено 13 августа 2011 г.

[1]

[2]

[3]

[4]