Составная кривая Безье

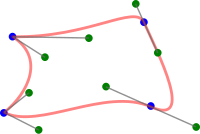
Безье — красный безье проходит через синие вершины, зеленые точки — это контрольные точки, определяющие форму соединяющихся кривых Безье.

В геометрическом моделировании и компьютерной графике составная кривая Безье или сплайн Безье — это сплайн, составленный из кривых Безье , который имеет не менее $C^{0}$ непрерывный . Другими словами, составная кривая Безье — это серия кривых Безье, соединенных концами, где последняя точка одной кривой совпадает с начальной точкой следующей кривой. В зависимости от применения могут предъявляться дополнительные требования к гладкости (например, $C^{1}$ или $C^{2}$ непрерывность) можно добавить. ^{[ 1 ]}

Непрерывный составной Безье также называется полибезье по сходству с ломаной линией , но в то время как в полилиниях точки соединены прямыми линиями, в полибезье точки соединены кривыми Безье. Безьегон кривых (также называемый безигоном ) — это замкнутый путь, составленный из Безье . Он похож на многоугольник тем, что соединяет набор вершин линиями, но если в многоугольниках вершины соединены прямыми линиями, то в безьергоне вершины соединены кривыми Безье. ^{[ 2 ]}^{[ 3 ]}^{[ 4 ]} Некоторые авторы даже называют $C^{0}$ составная кривая Безье - «сплайн Безье»; ^{[ 5 ]} последний термин, однако, используется другими авторами как синоним (несоставной) кривой Безье, и они добавляют слово «составной» перед «сплайном Безье», чтобы обозначить составной случай. ^{[ 6 ]}

Возможно, наиболее распространенным применением составного Безье является описание контура каждой буквы в файле PostScript или PDF . Такие контуры состоят из одного безьергона для открытых букв или из нескольких безьергонов для закрытых букв. Современные векторной графики и компьютерных шрифтов, системы такие как PostScript , Asymptote , Metafont , OpenType и SVG, используют составные кривые Безье, состоящие из кубических кривых Безье (кривые 3-го порядка) для рисования изогнутых форм.

Плавное соединение

Обычно желаемым свойством сплайнов является соединение отдельных кривых с заданным уровнем параметрической или геометрической непрерывности . Хотя отдельные кривые сплайна полностью $C^{\infty }$ непрерывны в пределах своего интервала, всегда существует некоторый разрыв в местах пересечения разных кривых.

Сплайн Безье уникален тем, что это один из немногих сплайнов, который не гарантирует более высокую степень непрерывности, чем $C^{0}$ . Однако можно организовать контрольные точки, чтобы гарантировать различные уровни непрерывности соединений, хотя это может привести к потере локального контроля, если ограничение слишком строгое для данной степени сплайна Безье.

Плавное соединение кубического Безье

Даны две кубические кривые Безье с контрольными точками. $[\mathbf {P} _{0},\mathbf {P} _{1},\mathbf {P} _{2},\mathbf {P} _{3}]$ и $[\mathbf {P} _{3},\mathbf {P} _{4},\mathbf {P} _{5},\mathbf {P} _{6}]$ соответственно, ограничения для обеспечения непрерывности при $\mathbf {P} _{3}$ можно определить следующим образом:

$C^{0}/G^{0}$ (позиционная непрерывность) требует, чтобы они встречались в одной и той же точке, что по определению делают все сплайны Безье. В этом примере общей точкой является $\mathbf {P} _{3}$

$C^{1}$ (непрерывность скорости) требует, чтобы соседние контрольные точки вокруг соединения были зеркалами друг друга. Другими словами, они должны следовать ограничению $\mathbf {P} _{4}=2\mathbf {P} _{3}-\mathbf {P} _{2}$

$G^{1}$ (непрерывность касательной) требует, чтобы соседние контрольные точки были коллинеарны соединению. Это менее строго, чем $C^{1}$ непрерывность, оставляя дополнительную степень свободы, которую можно параметризовать с помощью скаляра $\beta _{1}$ . Тогда ограничение может быть выражено выражением $\mathbf {P} _{4}=\mathbf {P} _{3}+(\mathbf {P} _{3}-\mathbf {P} _{2})\beta _{1}$

Хотя возможны следующие ограничения непрерывности, они редко используются с кубическими сплайнами Безье, поскольку другие сплайны, такие как B-сплайн или β-сплайн ^{[ 7 ]} естественно будет обрабатывать более высокие ограничения без потери локального контроля.

$C^{2}$ (непрерывность ускорения) ограничена $\mathbf {P} _{5}=\mathbf {P} _{1}+4(\mathbf {P} _{3}-\mathbf {P} _{2})$ . Однако применение этого ограничения ко всему кубическому сплайну Безье приведет к каскадной потере локального контроля над точками касания. Кривая по-прежнему будет проходить через каждую третью точку сплайна, но контроль над ее формой будет потерян. Чтобы достичь $C^{2}$ непрерывности с использованием кубических кривых, вместо этого рекомендуется использовать кубический однородный B-сплайн, поскольку это обеспечивает $C^{2}$ непрерывность без потери местного контроля за счет отсутствия гарантии прохождения через определенные точки

$G^{2}$ (непрерывность кривизны) ограничена $\mathbf {P} _{5}=\mathbf {P} _{3}+(\mathbf {P} _{3}-\mathbf {P} _{2})(2\beta _{1}+\beta _{1}^{2}+\beta _{2}/2)+(\mathbf {P} _{1}-\mathbf {P} _{2})\beta _{1}^{2}$ , оставляя две степени свободы по сравнению с $C^{2}$ , в виде двух скаляров $\beta _{1}$ и $\beta _{2}$ . Возможна более высокая степень геометрической непрерывности, хотя она становится все более сложной. ^{[ 8 ]}

$C^{3}$ (непрерывность толчка) ограничена $\mathbf {P} _{6}=\mathbf {P} _{3}+(\mathbf {P} _{3}-\mathbf {P} _{0})+6(\mathbf {P} _{1}-\mathbf {P} _{2}+\mathbf {P} _{3}-\mathbf {P} _{2})$ . Применение этого ограничения к кубическому сплайну Безье приведет к полной потере локального управления, поскольку весь сплайн теперь полностью ограничен и определяется контрольными точками первой кривой. Фактически, это, возможно, больше не сплайн, поскольку его форма теперь эквивалентна бесконечной экстраполяции первой кривой, что делает ее не только $C^{3}$ непрерывно, но $C^{\infty }$ , поскольку соединения между отдельными кривыми больше не существуют

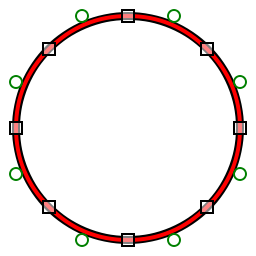
Аппроксимация дуг окружности

Если примитивы дуг окружности не поддерживаются в конкретной среде, их можно аппроксимировать кривыми Безье . ^{[ 9 ]} Обычно восемь квадратных сегментов ^{[ 10 ]} или четыре кубических сегмента используются для аппроксимации круга. Желательно найти длину $\mathbf {k}$ контрольных точек, которые приводят к наименьшей ошибке аппроксимации для заданного количества кубических сегментов.

Использование четырех кривых

углом 90 градусов Учитывая только единичную дугу окружности с в первом квадранте , мы определяем конечные точки $\mathbf {A}$ и $\mathbf {B}$ с контрольными точками $\mathbf {A'}$ и $\mathbf {B'}$ соответственно, как:

{\begin{aligned}\mathbf {A} &=[0,1]\\\mathbf {A'} &=[\mathbf {k} ,1]\\\mathbf {B'} &=[1,\mathbf {k} ]\\\mathbf {B} &=[1,0]\\\end{aligned}}

Из определения кубической кривой Безье имеем:

\mathbf {C} (t)=(1-t)^{3}\mathbf {A} +3(1-t)^{2}t\mathbf {A'} +3(1-t)t^{2}\mathbf {B'} +t^{3}\mathbf {B}

С точки зрения $\mathbf {C} (t=0.5)$ в качестве средней точки дуги мы можем написать следующие два уравнения:

{\begin{aligned}\mathbf {C} &={\frac {1}{8}}\mathbf {A} +{\frac {3}{8}}\mathbf {A'} +{\frac {3}{8}}\mathbf {B'} +{\frac {1}{8}}\mathbf {B} \\\mathbf {C} &={\sqrt {1/2}}={\sqrt {2}}/2\end{aligned}}

Решение этих уравнений для координаты x (и тождественно для координаты y) дает:

{\frac {0}{8}}\mathbf {+} {\frac {3}{8}}\mathbf {k} +{\frac {3}{8}}+{\frac {1}{8}}={\sqrt {2}}/2

\mathbf {k} ={\frac {4}{3}}({\sqrt {2}}-1)\approx 0.5522847498

Однако обратите внимание, что полученная кривая Безье полностью находится за пределами круга с максимальным отклонением радиуса около 0,00027. Добавляя небольшую поправку к промежуточным точкам, таким как

{\begin{aligned}\mathbf {A'} &=[\mathbf {k} +0.0009,1-0.00103]\\\mathbf {B'} &=[1-0.00103,\mathbf {k} +0.0009],\end{aligned}}

величина отклонения радиуса до 1 уменьшается примерно в 3 раза, до 0,000068 (за счет выводимости аппроксимируемой окружной кривой в конечных точках).

Общий случай

Мы можем аппроксимировать круг радиуса $R$ из произвольного числа кубических кривых Безье. Пусть дуга начинается в точке $\mathbf {A}$ и закончить в точке $\mathbf {B}$ , расположенный на равных расстояниях выше и ниже оси X, охватывающий дугу угла $\theta =2\phi$ :

{\begin{aligned}\mathbf {A} _{x}&=R\cos(\phi )\\\mathbf {A} _{y}&=R\sin(\phi )\\\mathbf {B} _{x}&=\mathbf {A} _{x}\\\mathbf {B} _{y}&=-\mathbf {A} _{y}\end{aligned}}

Контрольные точки могут быть записаны как: ^{[ 11 ]}

{\begin{aligned}\mathbf {A'} _{x}&={\frac {4R-\mathbf {A} _{x}}{3}}\\\mathbf {A'} _{y}&={\frac {(R-\mathbf {A} _{x})(3R-\mathbf {A} _{x})}{3\mathbf {A} _{y}}}\\\mathbf {B'} _{x}&=\mathbf {A'} _{x}\\\mathbf {B'} _{y}&=-\mathbf {A'} _{y}\end{aligned}}

Примеры

Восьмисегментный квадратичный полибезье (красный), аппроксимирующий окружность (черный) с контрольными точками
Четырехсегментный кубический полибезье (красный), аппроксимирующий круг (черный) с контрольными точками

Шрифты

В шрифтах TrueType используются составные кривые Безье, состоящие из квадратичных кривых Безье (кривые 2-го порядка). Чтобы описать типичный дизайн шрифта в виде компьютерного шрифта с любой заданной точностью, для Безье 3-го порядка требуется меньше данных, чем для Безье 2-го порядка; а для этого, в свою очередь, требуется меньше данных, чем для серии прямых линий. Это верно, даже несмотря на то, что любой сегмент прямой требует меньше данных, чем любой сегмент параболы; и этот параболический сегмент, в свою очередь, требует меньше данных, чем любой сегмент кривой 3-го порядка.

См. также

B-сплайн

Ссылки

^ Евгений Владимирович Шикин; Александр Иванович Плис (14 июля 1995 г.). Руководство по сплайнам для пользователя . ЦРК Пресс. п. 96. ИСБН 978-0-8493-9404-1 .
^ API-интерфейс Microsoft Polybezier
^ Справочник по API Papyrus beziergon
^ "Лучшая коробка с мелками" . ИнфоМир. 1991.
^ Ребаза, Хорхе (24 апреля 2012 г.). Первый курс прикладной математики . Джон Уайли и сыновья. ISBN 9781118277157 .
^ (Фирма), Wolfram Research (13 сентября 1996 г.). Стандартные дополнительные пакеты Mathematica® 3.0 . Издательство Кембриджского университета. ISBN 9780521585859 .
^ Гудман, TNT (9 декабря 1983 г.). «Свойства β-сплайнов» . Журнал теории приближения . 44 (2): 132–153. дои : 10.1016/0021-9045(85)90076-0 .
^ ДеРоуз, Энтони Д. (1 августа 1985 г.). «Геометрическая непрерывность: независимая от параметризации мера непрерывности для компьютерного геометрического проектирования» .
^ Станислав, Г. Адам. «Рисование круга с помощью кривых Безье» . Проверено 10 апреля 2010 г.
^ «Оцифровка буквенных конструкций» . Яблоко . Проверено 26 июля 2014 г.
^ ДеВенеза, Ричард. «Рисование круга с помощью кривых Безье» (PDF) . Проверено 10 апреля 2010 г.

[ShikinPlis1995-1] Евгений Владимирович Шикин; Александр Иванович Плис (14 июля 1995 г.). Руководство по сплайнам для пользователя . ЦРК Пресс. п. 96. ИСБН 978-0-8493-9404-1 .

[2] API-интерфейс Microsoft Polybezier

[3] Справочник по API Papyrus beziergon

[4] "Лучшая коробка с мелками" . ИнфоМир. 1991.

[5] Ребаза, Хорхе (24 апреля 2012 г.). Первый курс прикладной математики . Джон Уайли и сыновья. ISBN 9781118277157 .

[6] (Фирма), Wolfram Research (13 сентября 1996 г.). Стандартные дополнительные пакеты Mathematica® 3.0 . Издательство Кембриджского университета. ISBN 9780521585859 .

[7] Гудман, TNT (9 декабря 1983 г.). «Свойства β-сплайнов» . Журнал теории приближения . 44 (2): 132–153. дои : 10.1016/0021-9045(85)90076-0 .

[8] ДеРоуз, Энтони Д. (1 августа 1985 г.). «Геометрическая непрерывность: независимая от параметризации мера непрерывности для компьютерного геометрического проектирования» .

[9] Станислав, Г. Адам. «Рисование круга с помощью кривых Безье» . Проверено 10 апреля 2010 г.

[10] «Оцифровка буквенных конструкций» . Яблоко . Проверено 26 июля 2014 г.

[11] ДеВенеза, Ричард. «Рисование круга с помощью кривых Безье» (PDF) . Проверено 10 апреля 2010 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]