Реакция на столкновение

В контексте классического механического моделирования и физических движков, используемых в видеоиграх , реакция на столкновение связана с моделями и алгоритмами для моделирования изменений в движении двух твердых тел после столкновения и других форм контакта.

Жесткий контакт с телом

Фазы сжатия и расширения при столкновении двух твердых тел.

Два твердых тела, находящихся в неограниченном движении, потенциально под действием сил, можно смоделировать путем решения их уравнений движения с использованием методов численного интегрирования . При столкновении кинетические свойства двух таких тел, кажется, претерпевают мгновенное изменение, обычно приводящее к тому, что тела отскакивают друг от друга, скользят или вступают в относительный статический контакт, в зависимости от упругости материалов и конфигурации столкновения. .

Контактные силы

Происхождение явления отскока, или реакции , можно объяснить поведением реальных тел, которые, в отличие от своих идеально жестких идеализированных аналогов, подвергаются незначительному сжатию при столкновении с последующим расширением перед разделением. Фаза сжатия преобразует кинетическую энергию тел в потенциальную энергию и, в некоторой степени, в тепло. Фаза расширения преобразует потенциальную энергию обратно в кинетическую энергию.

Во время фаз сжатия и расширения двух сталкивающихся тел каждое тело генерирует реактивные силы на другое в точках контакта, так что сумма сил реакции одного тела равна по величине, но противоположна по направлению силам другого, как согласно ньютоновскому принципу действия и противодействия. Если пренебречь эффектами трения, то столкновение рассматривается как затрагивающее только ту составляющую скорости, которая направлена ​​вдоль нормали контакта, а тангенциальные составляющие остаются неизменными.

Реакция

Степень относительной кинетической энергии, сохраняемой после столкновения, называемая восстановлением , зависит от упругости материалов тел. Коэффициент восстановления между двумя данными материалами моделируется как соотношение $e\in [0..1]$ относительной скорости точки контакта вдоль нормали контакта после столкновения по отношению к относительной скорости той же точки вдоль той же нормали до столкновения. Эти коэффициенты обычно определяются эмпирически для различных пар материалов, например, дерева и бетона или резины и дерева. Значения для $e$ значения, близкие к нулю, указывают на неупругие столкновения, такие как удар куска мягкой глины об пол, тогда как значения, близкие к единице, соответствуют высокоэластичным столкновениям, например, когда резиновый мяч отскакивает от стены. Потери кинетической энергии происходят относительно одного тела по отношению к другому. Таким образом, общий импульс обоих тел относительно некоторой общей точки отсчета не изменяется после столкновения, что соответствует принципу сохранения импульса .

Трение

Трение из-за дефектов микроструктуры поверхности.

Еще одним важным явлением контакта является трение между поверхностями, сила, которая препятствует относительному движению двух контактирующих поверхностей или тела в жидкости. В этом разделе мы обсуждаем трение между поверхностями двух тел, находящихся в относительном статическом контакте или скользящем контакте. В реальном мире трение возникает из-за несовершенной микроструктуры поверхностей, выступы которых сцепляются друг с другом, создавая реактивные силы, касательные к поверхностям.

Чтобы преодолеть трение между двумя телами, находящимися в статическом контакте, поверхности должны каким-то образом оторваться друг от друга. В движении степень сродства поверхности снижается, и, следовательно, тела, находящиеся в скользящем движении, имеют тенденцию оказывать меньшее сопротивление движению. Эти две категории трения называются соответственно статическим трением и динамическим трением .

Приложенная сила

Это сила, которая прикладывается к объекту другим объектом или человеком.направление приложенной силы зависит от того, как приложена сила.

Нормальная сила

Это опорная сила, действующая на объект, находящийся в контакте с другим.стабильный объект. Нормальную силу иногда называют силой давления, поскольку онадействие сжимает поверхности вместе. Нормальная сила всегда направлена ​​в сторонуобъект и действует перпендикулярно приложенной силе.

Сила трения

Это сила, действующая на поверхность, когда объект движется по ней или прилагает усилие.чтобы перебраться через него. Сила трения препятствует движению объекта. Результаты трениякогда две поверхности плотно прижимаются друг к другу, вызывая силы притяжения между молекуламимежду молекулами двух разных поверхностей. Таким образом, трение зависит отот природы двух поверхностей и от степени, в которой они прижаты друг к другу.Трение всегда действует параллельно контактирующей поверхности и противоположно направлениюдвижение. Силу трения можно рассчитать с помощью уравнения.

Импульсная контактная модель

Сила $\mathbf {f} (t)\in \mathbb {R} ^{3}$, в зависимости от времени $t\in \mathbb {R}$, действующий на тело предполагаемой постоянной массы $m\in \mathbb {R}$ на временной интервал $\lbrack t_{0},t_{1}\rbrack$ вызывает изменение импульса тела $\mathbf {p} (t)=m\mathbf {v} (t)$, где $\mathbf {v} (t)$ результирующее изменение скорости. Изменение импульса, называемое импульсом и обозначаемое $\mathbf {j} \in \mathbb {R} ^{3}$ таким образом вычисляется как

$\mathbf {j} =\int _{t_{0}}^{t_{1}}\mathbf {f} dt$

Для фиксированного импульса $\mathbf {j}$, уравнение предполагает, что $t_{1}\rightarrow t_{0}\Rightarrow \left|\mathbf {f} \right|\rightarrow \infty$, то есть меньший интервал времени должен быть компенсирован более сильной силой реакции для достижения того же импульса. При моделировании столкновения между идеализированными твердыми телами нецелесообразно моделировать фазы сжатия и расширения геометрии тела в течение интервала времени столкновения. Однако, если предположить, что сила $\mathbf {f}$ можно найти то, что равно $0$ везде, кроме $t_{0}$, и такой, что предел

$\lim _{t_{1}\rightarrow t_{0}}\int _{t_{0}}^{t_{1}}\mathbf {f} dt$

существует и равен $\mathbf {j}$, понятие мгновенных импульсов может быть введено для моделирования мгновенного изменения скорости после столкновения.

Модель импульсной реакции

Применение импульсов в точке столкновения

Эффект силы реакции $\mathbf {f} _{r}(t)\in \mathbb {R} ^{3}$ за интервал столкновения $[t_{0},t_{1}]$ следовательно, может быть представлен мгновенным импульсом реакции $\mathbf {j} _{r}(t)\in \mathbb {R} ^{3}$, вычисляется как

$\mathbf {j} _{r}=\int _{t_{0}}^{t_{1}}\mathbf {f} _{r}dt$

По вычету из принципа действия и противодействия, если импульс столкновения, приложенный первым телом ко второму телу в точке контакта $\mathbf {p} _{r}\in \mathbb {R} ^{3}$ является $\mathbf {j} _{r}$, встречный импульс, приложенный вторым телом к ​​первому, равен $-\mathbf {j} _{r}$. Разложение $\pm \mathbf {j} _{r}=\pm j_{r}\mathbf {\hat {n}}$ в величину импульса $j_{r}\in \mathbb {R}$ и направление вдоль нормали контакта $\mathbf {\hat {n}}$ и его отрицание $-\mathbf {\hat {n}}$ позволяет вывести формулу для расчета изменения линейной и угловой скоростей тел в результате ударных импульсов. В последующих формулах $\mathbf {\hat {n}}$ всегда предполагается, что он направлен от тела 1 к телу 2 в точке контакта.

Предполагая величину импульса столкновения $j_{r}$ задано, и используя законы движения Ньютона, соотношение между предлинейными и постлинейными скоростями тел таково:

	$\mathbf {v'} _{1}=\mathbf {v} _{1}-{\frac {j_{r}}{m_{1}}}\mathbf {\hat {n}}$	(1а)
	$\mathbf {v'} _{2}=\mathbf {v} _{2}+{\frac {j_{r}}{m_{2}}}\mathbf {\hat {n}}$	(1б)

где, для $i$тело, $\mathbf {v} _{i}\in \mathbb {R} ^{3}$ - линейная скорость перед столкновением, $\mathbf {v'} _{i}\in \mathbb {R} ^{3}$ — линейная скорость после столкновения.

Аналогично для угловых скоростей

	$\mathbf {\omega '} _{1}=\mathbf {\omega } _{1}-j_{r}\mathbf {I} _{1}^{-1}(\mathbf {r} _{1}\times \mathbf {\hat {n}} )$	(2а)
	$\mathbf {\omega '} _{2}=\mathbf {\omega } _{2}+j_{r}\mathbf {I} _{2}^{-1}(\mathbf {r} _{2}\times \mathbf {\hat {n}} )$	(2б)

где, для $i$тело, ${\omega }_{i}\in \mathbb {R} ^{3}$ - угловая скорость перед столкновением, ${\omega '}_{i}\in \mathbb {R} ^{3}$ - угловая скорость после столкновения, $\mathbf {I} _{i}\in \mathbb {R} ^{3\times 3}$ - тензор инерции в мировой системе отсчета, а $\mathbf {r} _{i}\in \mathbb {R} ^{3}$ это смещение общей точки контакта $\mathbf {p}$ от центра масс.

Скорости $v_{p1},v_{p2}\in \mathbb {R} ^{3}$ тел в точке контакта можно вычислить через соответствующие линейные и угловые скорости, используя

$\mathbf {v} _{pi}=\mathbf {v} _{i}+\mathbf {\omega } _{i}\times \mathbf {r} _{i}$

(3)

для $i=1,2$. Коэффициент реституции $e$ связывает относительную скорость до столкновения $\mathbf {v} _{r}=\mathbf {v} _{p2}-\mathbf {v} _{p1}$ точки контакта к относительной скорости после столкновения $\mathbf {v'} _{r}=\mathbf {v'} _{p2}-\mathbf {v'} _{p1}$ по нормали контакта $\mathbf {\hat {n}}$ следующее

$\mathbf {v'} _{r}\cdot \mathbf {\hat {n}} =-e\mathbf {v} _{r}\cdot \mathbf {\hat {n}}$

(4)

Подставляя уравнения (1a), (1b), (2a), (2b) и (3) в уравнение (4) и находя величину импульса реакции. $j_{r}$ урожайность

$j_{r}={\frac {-(1+e)\mathbf {v} _{r}\cdot \mathbf {\hat {n}} }{{m_{1}}^{-1}+{m_{2}}^{-1}+({\mathbf {I} _{1}}^{-1}(\mathbf {r} _{1}\times \mathbf {\hat {n}} )\times \mathbf {r} _{1}+{\mathbf {I} _{2}}^{-1}(\mathbf {r} _{2}\times \mathbf {\hat {n}} )\times \mathbf {r} _{2})\cdot \mathbf {\hat {n}} }}$

(5)

Вычисление импульсной реакции

Таким образом, процедура расчета линейных скоростей после столкновения $\mathbf {v'} _{i}$ и угловые скорости $\mathbf {\omega '} _{i}$ заключается в следующем:

1. Вычислите величину импульса реакции $j_{r}$ с точки зрения $\mathbf {v} _{r}$, $m_{1}$, $m_{2}$, $\mathbf {I} _{1}$, $\mathbf {I} _{2}$, $\mathbf {r} _{1}$, $\mathbf {r} _{2}$, $\mathbf {\hat {n}}$ и $e$ используя уравнение (5)
2. Вычислите вектор импульса реакции $\mathbf {j} _{r}$ по своей величине $j_{r}$ и контакт нормальный $\mathbf {\hat {n}}$ с использованием $\mathbf {j} _{r}=j_{r}\mathbf {\hat {n}}$.
3. Вычислите новые линейные скорости $\mathbf {v'} _{i}$ в плане старых скоростей $\mathbf {v} _{i}$, массы $m_{i}$ и вектор импульса реакции $\mathbf {j} _{r}$ используя уравнения (1a) и (1b)
4. Вычислите новые угловые скорости $\mathbf {\omega '} _{i}$ в терминах старых угловых скоростей $\mathbf {\omega } _{i}$, тензоры инерции $\mathbf {I} _{i}$ и импульс реакции $j_{r}$ используя уравнения (2a) и (2b)

Импульсная модель трения

Модель кулоновского трения - конус трения

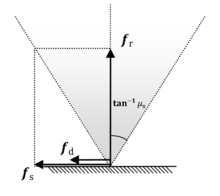
Одной из наиболее популярных моделей описания трения является модель трения Кулона . Эта модель определяет коэффициенты статического трения. ${\mu }_{s}\in \mathbb {R}$ и динамическое трение ${\mu }_{d}\in \mathbb {R}$ такой, что ${\mu }_{s}>{\mu }_{d}$. Эти коэффициенты описывают два типа сил трения с точки зрения сил реакции, действующих на тела. Более конкретно, статические и динамические величины силы трения. $f_{s},f_{d}\in \mathbb {R}$ рассчитываются через величину силы реакции $f_{r}=|\mathbf {f} _{r}|$ следующее

	$f_{s}={\mu }_{s}f_{r}$	(6а)
	$f_{d}={\mu }_{d}f_{r}$	(6б)

Значение $f_{s}$ определяет максимальную величину силы трения, необходимой для противодействия тангенциальной составляющей любой внешней суммарной силы, приложенной к относительно статичному телу, так что оно остается статичным. Таким образом, если внешняя сила достаточно велика, статическое трение не может полностью противостоять этой силе, после чего тело набирает скорость и становится подверженным динамическому трению величиной $f_{d}$ действует против скорости скольжения.

Модель кулоновского трения эффективно определяет конус трения , внутри которого тангенциальной составляющей силы, действующей со стороны одного тела на поверхность другого при статическом контакте, противодействует равная и противоположная сила, так что статическая конфигурация сохраняется. И наоборот, если сила выходит за пределы конуса, статическое трение уступает место динамическому трению.

Учитывая, что контакт нормальный $\mathbf {\hat {n}} \in \mathbb {R} ^{3}$ и относительная скорость $\mathbf {v} _{r}\in \mathbb {R} ^{3}$ точки контакта, касательный вектор $\mathbf {\hat {t}} \in \mathbb {R} ^{3}$, ортогональный $\mathbf {\hat {n}}$, можно определить так, что

$\mathbf {\hat {t}} =\left\{{\begin{matrix}{\frac {\mathbf {v} _{r}-(\mathbf {v} _{r}\cdot \mathbf {\hat {n}} )\mathbf {\hat {n}} }{|\mathbf {v} _{r}-(\mathbf {v} _{r}\cdot \mathbf {\hat {n}} )\mathbf {\hat {n}} |}}&\mathbf {v} _{r}\cdot \mathbf {\hat {n}} \neq 0&\\{\frac {\mathbf {f} _{e}-(\mathbf {f} _{e}\cdot \mathbf {\hat {n}} )\mathbf {\hat {n}} }{|\mathbf {f} _{e}-(\mathbf {f} _{e}\cdot \mathbf {\hat {n}} )\mathbf {\hat {n}} |}}&\mathbf {v} _{r}\cdot \mathbf {\hat {n}} =0&\mathbf {f} _{e}\cdot \mathbf {\hat {n}} \neq 0\\\mathbf {0} &\mathbf {v} _{r}\cdot \mathbf {\hat {n}} =0&\mathbf {f} _{e}\cdot \mathbf {\hat {n}} =0\\\end{matrix}}\right.$

(7)

где $\mathbf {f} _{e}\in \mathbb {R} ^{3}$ представляет собой сумму всех внешних сил, действующих на тело. Многовариантное определение $\mathbf {\hat {t}}$ требуется для надежного расчета фактической силы трения $\mathbf {f} _{f}\in \mathbb {R} ^{3}$ как для общего, так и для частного состояния контакта. Неформально, в первом случае вычисляет касательный вектор вдоль компонента относительной скорости, перпендикулярного нормали контакта. $\mathbf {\hat {n}}$. Если этот компонент равен нулю, второй случай выводит $\mathbf {\hat {t}}$ через касательную составляющую внешней силы $\mathbf {f} _{e}\in \mathbb {R} ^{3}$. Если нет тангенциальной скорости или внешних сил, то трение не предполагается и $\mathbf {\hat {t}}$ может быть установлен в нулевой вектор. Таким образом, $\mathbf {f} _{f}\in \mathbb {R} ^{3}$ вычисляется как

$\mathbf {f} _{f}=\left\{{\begin{matrix}-(\mathbf {f} _{e}\cdot \mathbf {\hat {t}} )\mathbf {\hat {t}} &\mathbf {v} _{r}\cdot \mathbf {\hat {t}} =0&\mathbf {f} _{e}\cdot \mathbf {\hat {t}} \leq f_{s}\\-f_{d}\mathbf {\hat {t}} &{\text{(otherwise)}}\\\end{matrix}}\right.$

(8)

Уравнения (6a), (6b), (7) и (8) описывают модель кулоновского трения в терминах сил. Адаптировав аргумент в пользу мгновенных импульсов, можно вывести основанную на импульсах версию модели кулоновского трения, связывающую импульс трения $\mathbf {j} _{f}\in \mathbb {R} ^{3}$, действуя по касательной $\mathbf {\hat {t}}$, к импульсу реакции $\mathbf {j} _{r}\in \mathbb {R} ^{3}$. Интегрирование (6a) и (6b) по интервалу времени столкновения $[t_{0}..t_{1}]$ урожайность

	$j_{s}={\mu }_{s}j_{r}$	(9а)
	$j_{d}={\mu }_{d}j_{r}$	(9б)

где $j_{r}=|\mathbf {j} _{r}|$ - величина реактивного импульса, действующего по нормали контакта $\mathbf {\hat {n}}$. Аналогично, предполагая $\mathbf {\hat {t}}$ постоянна на всем интервале времени, интегрирование (8) дает

$\mathbf {j} _{f}=\left\{{\begin{matrix}-(m\mathbf {v} _{r}\cdot \mathbf {\hat {t}} )\mathbf {\hat {t}} &\mathbf {v} _{r}\cdot \mathbf {\hat {t}} =0&m\mathbf {v} _{r}\cdot \mathbf {\hat {t}} \leq j_{s}\\-j_{d}\mathbf {\hat {t}} &{\text{(otherwise)}}\\\end{matrix}}\right.$

(10)

Уравнения (5) и (10) определяют модель контакта на основе импульсов, которая идеально подходит для моделирования на основе импульсов. При использовании этой модели необходимо внимательно подходить к выбору ${\mu }_{s}$ и ${\mu }_{d}$ поскольку более высокие значения могут внести в систему дополнительную кинетическую энергию.

См. также

• Обнаружение столкновений

Ссылки

• К. Велла, «Gravitas: расширяемая структура физического движка, использующая принципы объектно-ориентированной и основанной на шаблонах проектирования архитектуры программного обеспечения», магистерская диссертация в области информационных технологий, Мальтийский университет, Мсида, 2008 г.