Тест на изоморфизм графов Вейсфейлера-Лемана

В теории графов — тест на изоморфизм графов Вейсфейлера-Лемана эвристический тест на существование изоморфизма между двумя графами G и H. это Это обобщение алгоритма улучшения цвета , впервые описанное Вейсфейлером и Леманом в 1968 году. Оригинальная формулировка основана на канонизации графов — нормальной форме графов, при этом существует также комбинаторная интерпретация в духе уточнения цвета и связи с логикой.

Существует несколько версий теста (например, k-WL и k-FWL), называемых в литературе под разными названиями, что легко приводит к путанице. Кроме того, в нескольких старых статьях Андрей Леман пишется как «Леман».

Эвристика изоморфизма графов на основе Вейсфейлера-Лемана

Все варианты уточнения цвета представляют собой односторонние эвристики, которые принимают на вход два графа G и H и выдают сертификат, что они разные или «не знаю». Это означает, что если эвристика способна отличить G и H , то они заведомо различны, но другое направление не имеет места: для каждого варианта WL-теста (см. ниже) существуют неизоморфные графы, в которых разница не обнаружен. Эти графы представляют собой высокосимметричные графы, такие как обычные графы для уточнения 1-WL/цвет.

1-мерный Вейсфейлер-Леман (1-WL)

Тест на изоморфизм одномерного графа по существу аналогичен алгоритму уточнения цвета (разница связана с отсутствием ребер и не имеет значения для всех практических целей, поскольку легко увидеть, что графы с различным количеством узлов не являются ребрами). изоморфный). Алгоритм действует следующим образом:

Инициализация. Все узлы инициализируются одним и тем же цветом 0.

Уточнение Два узла u,v получают разный цвет, если а) раньше у них был другой цвет или б) существует цвет c такой, что u и v имеют разное количество c соседей цвета .

Завершение Алгоритм завершается, если разделение, вызванное двумя последовательными шагами уточнения, одинаково.

Чтобы использовать этот алгоритм в качестве теста на изоморфизм графа, алгоритм запускается на двух входных графах G и H параллельно, т.е. при разделении используются цвета, так что некоторый цвет c (после одной итерации) может означать «узел ровно с 5 соседи цвета 0'. На практике это достигается за счет уточнения цвета графа непересекающегося G и H. объединения Затем можно посмотреть на гистограмму цветов обоих графов (подсчитав количество узлов после стабилизации уточнения цвета) и если они различаются, то это свидетельство того, что оба графа не изоморфны.

Алгоритм завершает работу не позднее, чем через $n-1$ раунды, где $n$ — это количество узлов входного графа, поскольку на каждом этапе уточнения ему приходится разбивать один раздел, и это может происходить максимум до тех пор, пока каждый узел не получит свой собственный цвет. Обратите внимание, что существуют графы, для которых требуется такое количество итераций, хотя на практике количество раундов до завершения имеет тенденцию быть очень низким (<10).

Уточнение раздела на каждом этапе осуществляется путем обработки для каждого узла его метки и меток его ближайших соседей. Поэтому WLtest можно рассматривать как алгоритм передачи сообщений , который также связывает его с графовыми нейронными сетями .

Вейсфейлера-Лемана высшего порядка

Именно здесь появляются два вышеупомянутых варианта алгоритма WL. И k -мерный алгоритм Вейсфейлера-Лемана (k-WL), и k -мерный фольклорный алгоритм Вейсфейлера-Лемана (k-FWL) являются расширениями 1-WL сверху, работающими с k-кортежами вместо отдельных узлов. Хотя их различие на первый взгляд выглядит невинным, можно показать, что k-WL и (k-1)-FWL (при k>2) различают одни и те же пары графов.

k-WL (k>1)

Input: a graph G = (V,E)
# initialize
$c^{0}({\bar {v}})={\text{Hash}}({\text{type}}({\bar {v}}))$ for all ${\bar {v}}\in V^{k}$
repeat
   $c_{i}^{\ell }({\bar {v}})=\{\!\{c^{\ell -1}({\bar {w}}):{\bar {w}}\in {\mathcal {N}}_{i}({\bar {v}})\}\!\}$ for all ${\bar {v}}\in V^{k},i\in [k]$
   $c^{\ell }({\bar {v}})={\text{Hash}}(c^{\ell -1}({\bar {v}}),c_{1}^{\ell }({\bar {v}}),\dots ,c_{k}^{\ell }({\bar {v}})$
until $c^{\ell }\equiv c^{\ell -1}$ (both colorings induce identical partitions of $V^{k}$)
return $c^{\ell }$

Здесь окрестности ${\mathcal {N}}_{i}({\bar {v}})$ из k-кортежа ${\bar {v}}$ задается набором всех k-кортежей, достижимых путем замены i-й позиции ${\bar {v}}$: ${\mathcal {N}}_{i}({\bar {v}})=\{(v_{1},\dots ,v_{i-1},w,v_{i+1},\dots ,v_{k}):w\in V\}$ Атомный тип ${\text{type}}({\bar {v}})$кортежа кодирует информацию о ребрах между всеми парами узлов из ${\bar {v}}$. Например, кортеж из двух элементов имеет только два возможных атомарных типа, а именно, два узла могут иметь общее ребро или нет. Обратите внимание, что если граф имеет несколько (разных) отношений ребер или дополнительные узлы, членство в них также представлено в ${\text{type}}({\bar {v}})$.

Основная идея k-WL состоит в том, чтобы расширить понятие окрестности до k-кортежей, а затем эффективно выполнить уточнение цвета полученного графа.

k-FWL (k>1)

Input: a graph G = (V,E)
# initialize
$c^{0}({\bar {v}})={\text{Hash}}({\text{type}}({\bar {v}})$) for all ${\bar {v}}\in V^{k}$
repeat
  $c_{w}^{\ell }({\bar {v}})={\big (}c^{\ell -1}({\bar {v}}[1]\!\!\leftarrow \!w),\dots ,c^{\ell -1}({\bar {v}}[k]\!\!\leftarrow \!w){\big )}$ for all ${\bar {v}}\in V^{k},w\in V$
  $c^{\ell }({\bar {v}})={\text{Hash}}{\big (}c^{\ell -1}({\bar {v}}),\{\!\{c_{w}^{\ell }({\bar {v}}):w\in V\}\!\}{\big )}$
until $c^{\ell }\equiv c^{\ell -1}$ (both colorings induce identical partitions of $V^{k}$)
return $c^{\ell }$

Здесь ${\bar {v}}[i]\!\!\leftarrow \!w$ это кортеж ${\bar {v}}$ где i-я позиция заменяется на $w$.

Обратите внимание, что между k-WL и k-FWL есть одно существенное различие: k-FWL проверяет, что произойдет, если одиночный узел w помещен в любую позицию k-кортежа (а затем вычисляет мультимножество этих k-кортежей), в то время как k-WL смотрит на мультимножества, которые вы получаете при изменении i-го компонента только исходного k-кортежа. Затем он использует все эти мультимножества в хеше, который вычисляет новый цвет.

Можно показать (хотя и только через связь с логикой), что k-FWL и (k+1)-WL эквивалентны (для $k\geq 2$). Поскольку оба алгоритма экспоненциально масштабируются по k (оба перебирают все k-кортежи), использование k-FWL гораздо более эффективно, чем использование эквивалентного (k+1)-WL.

Примеры и код для 1-WL

Код

# ALGORITHM WLpairs
# INPUT: two graphs G and H to be tested for isomorphism
# OUTPUT: Certificates for G and H and whether they agree
U = combineTwo(G, H)
glabels = initializeLabels(U)  # dictionary where every node gets the same label 0
labels = {}  # dictionary that will provide translation from a string of labels of a node and its neighbors to an integer
newLabel = 1
done = False
while not(done):
    glabelsNew = {}  # set up the dictionary of labels for the next step
    for node in U:
        label = str(glabels[node]) + str([glabels[x] for x in neighbors of node].sort())
        if not(label in labels):  # a combination of labels from the node and its neighbors is encountered for the first time
            labels[label] = newLabel  # assign the string of labels to a new number as an abbreviated label
            newLabel += 1  # increase the counter for assigning new abbreviated labels
        glabelsNew[node] = labels[label]
    if (number of different labels in glabels) == (number of different labels in glabelsNew):
        done = True
    else:
        glabels = glabelsNew.copy()
certificateG = certificate for G from the sorted labels of the G-part of U
certificateH = certificate for H from the sorted labels of the H-part of U
if certificateG == certificateH:
    test = True
else:
    test = False

Вот реальный код Python , который включает описание первых примеров.

g5_00 = {0: {1, 2, 4}, 1: {0, 2}, 2: {0, 1, 3}, 3: {2, 4}, 4: {0, 3}}
g5_01 = {0: {3, 4}, 1: {2, 3, 4}, 2: {1, 3}, 3: {0, 1, 2}, 4: {0, 1}}
g5_02 = {0: {1, 2, 4}, 1: {0, 3}, 2: {0, 3}, 3: {1, 2, 4}, 4: {0, 3}}


def combineTwo(g1, g2):
    g = {}
    n = len(g1)
    for node in g1:
        s = set()
        for neighbor in g1[node]:
            s.add(neighbor)
        g[node] = s.copy()
    for node in g2:
        s = set()
        for neighbor in g2[node]:
            s.add(neighbor + n)
        g[node + n] = s.copy()
    return g


g = combineTwo(g5_00, g5_02)
labels = {}
glabels = {}
for i in range(len(g)):
    glabels[i] = 0
glabelsCount = 1
newlabel = 1

done = False
while not (done):
    glabelsNew = {}
    glabelsCountNew = 0
    for node in g:
        label = str(glabels[node])
        s2 = []
        for neighbor in g[node]:
            s2.append(glabels[neighbor])
        s2.sort()
        for i in range(len(s2)):
            label += "_" + str(s2[i])
        if not (label in labels):
            labels[label] = newlabel
            newlabel += 1
            glabelsCountNew += 1
        glabelsNew[node] = labels[label]
    if glabelsCount == glabelsCountNew:
        done = True
    else:
        glabelsCount = glabelsCountNew
        glabels = glabelsNew.copy()
print(glabels)

g0labels = []
for i in range(len(g0)):
    g0labels.append(glabels[i])
g0labels.sort()
certificate0 = ""
for i in range(len(g0)):
    certificate0 += str(g0labels[i]) + "_"
g1labels = []
for i in range(len(g1)):
    g1labels.append(glabels[i + len(g0)])
g1labels.sort()
certificate1 = ""
for i in range(len(g1)):
    certificate1 += str(g1labels[i]) + "_"

if certificate0 == certificate1:
    test = True
else:
    test = False
print("Certificate 0:", certificate0)
print("Certificate 1:", certificate1)
print("Test yields:", test)

Примеры

Первые три примера относятся к графам пятого порядка .

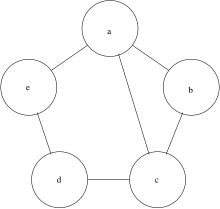
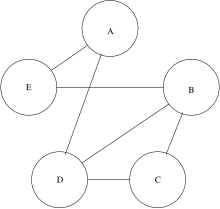
График G0	График G1	График G2

WLpair проходит 3 раунда на «G0» и «G1». Тест пройден успешно, как подтверждают сертификаты.

WLpair проходит 4 раунда на «G0» и «G2». Тест не пройден, поскольку сертификаты не совпадают. Действительно, «G0» имеет цикл длины 5, а «G2» — нет, поэтому «G0» и «G2» не могут быть изоморфными.

WLpair проходит 4 раунда на «G1» и «G2». Тест не пройден, поскольку сертификаты не совпадают. Из предыдущих двух случаев мы уже знаем $G_{1}\cong G_{0}\not \cong G_{2}$.

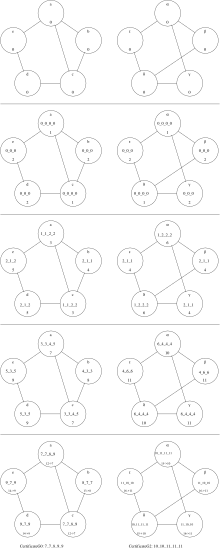
G0 против G1	G0 против G2	G1 против G2

Действительно, G0 и G1 изоморфны. Любой изоморфизм должен учитывать компоненты и, следовательно, метки. Это можно использовать для кернеризации проблемы изоморфизма графов. Обратите внимание, что не всякое отображение вершин, учитывающее метки, дает изоморфизм. Позволять $\varphi :G_{0}\rightarrow G_{1}$ и $\psi :G_{0}\rightarrow G_{1}$ быть картами, заданными $\varphi (a)=D,\varphi (b)=C,\varphi (c)=B,\varphi (d)=E,\varphi (e)=A$ соотв. $\psi (a)=B,\psi (b)=C,\psi (c)=D,\psi (d)=E,\psi (e)=A$. Пока $\varphi$ не является изоморфизмом $\psi$ представляет собой изоморфизм.

Применяя WLpair к G0 и G2, мы получаем для G0 сертификат 7_7_8_9_9 . Но изоморфный G1 получает сертификат 7_7_8_8_9 при применении WLpair к G1 и G2 . Это иллюстрирует феномен, связанный с метками, зависящими от порядка выполнения WLtest на узлах. Либо найти другой метод перемаркировки, сохраняющий уникальность меток, что становится довольно техническим, либо можно вообще пропустить перемаркировку и сохранить строки меток, что значительно увеличивает длину сертификата, либо применить WLtest к объединению двух протестированных сертификатов. графики, как мы это делали в варианте WLpair. Обратите внимание: хотя G1 и G2 могут получить разные сертификаты, когда WLtest выполняется для них отдельно, они получают один и тот же сертификат от WLpair.

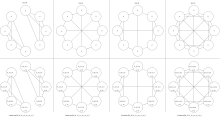
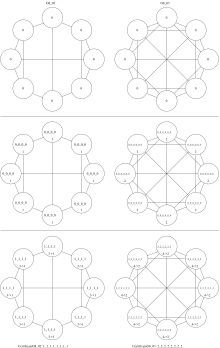
Следующий пример касается обычных графиков . WLtest не может различать регулярные графики одинакового порядка, но WLpair может различать регулярные графы различной степени , даже если они имеют один и тот же порядок. Фактически WLtest завершается после одного раунда, как видно в примерах порядка 8, все из которых являются 3-регулярными, за исключением последнего, который является 5-регулярным.

Все четыре графа попарно неизоморфны. G8_00 имеет два связных компонента, а остальные нет. G8_03 5-регулярный, остальные 3-регулярные. G8_01 не имеет 3-цикла, а G8_02 имеет 3-цикла.

WLtest применялся к четырем регулярным графам восьмого порядка.	WLpair применяется к G8_00 и G8_01 одинаковой степени.	WLpair применяется к G8_02 и G8_03 различной степени.

Еще один пример двух неизоморфных графов, которые WLpair не может различить, приведен здесь .

Приложения

Теория, лежащая в основе теста Вейсфейлера-Лемана, применяется в графовых нейронных сетях .

Ядра графа Вейсфейлера-Лемана

При машинном обучении нелинейных данных используются ядра для представления данных в многомерном пространстве признаков, после чего линейные методы, такие как машины опорных векторов можно применять . Данные, представленные в виде графиков, часто ведут себя нелинейно . Ядра графов — это метод предварительной обработки таких нелинейных данных на основе графов для упрощения последующих методов обучения. Такие ядра графа могут быть построены путем частичного выполнения теста Вейсфейлера-Лемана и обработки раздела, созданного к этому моменту. Эти ядра графов Вейсфейлера-Лемана привлекли значительное количество исследований в течение десятилетия после их публикации. Они также реализованы в специальных библиотеках для ядер графов, таких как GraKeL .

Обратите внимание, что ядра для искусственной нейронной сети в контексте машинного обучения , такие как ядра графов, не следует путать с ядрами, применяемыми в эвристических алгоритмах для снижения вычислительных затрат при решении задач высокой сложности, таких как примеры NP-сложных задач в полевых условиях. сложности теории . Как указано выше, тест Вейсфейлера-Лемана также можно применять и в более позднем контексте.

См. также

• Изоморфизм графа
• Графовая нейронная сеть