Феномен Стокса

В комплексном анализе явление Стокса , открытое Г. Г. Стоксом ( 1847 , 1858 ), заключается в том, что асимптотическое поведение функций может различаться в разных областях комплексной плоскости. По-видимому, это порождает парадокс при рассмотрении асимптотического разложения аналитической функции. Поскольку аналитическая функция непрерывна, можно ожидать, что асимптотическое разложение будет непрерывным. Этот парадокс является предметом ранних исследований Стокса и известен как феномен Стокса. Области комплексной плоскости с различным асимптотическим поведением ограничены, возможно, одним или двумя типами кривых, известных как кривые Стокса и антистоксовые кривые. Этот кажущийся парадокс с тех пор был разрешен, и было показано, что предполагаемый разрывный скачок в асимптотических разложениях является плавным и непрерывным. Чтобы разрешить этот парадокс, необходимо осторожно обращаться с асимптотическим разложением. Более конкретно, асимптотическое разложение должно включать дополнительные экспоненциально малые члены по сравнению с обычными алгебраическими членами, включенными в обычное асимптотическое разложение. В явлении Стокса происходит то, что асимптотическое разложение в одной области может содержать экспоненциально малый вклад (пренебрежение этим вкладом все равно дает правильное асимптотическое разложение для этой области). Однако этот экспоненциально малый член может стать экспоненциально большим в другой области комплексной плоскости, это изменение происходит поперек антистоксовых кривых. Более того, экспоненциально малый член может включать или выключать другие экспоненциально малые члены, это изменение происходит поперек кривой Стокса. Включение этих экспоненциально малых членов позволяет записать асимптотическое разложение как непрерывное разложение для всей комплексной области, что разрешает парадокс феномена Стокса.

Кривые Стокса и антистоксовые кривые

На кривой Стокса экспоненциально малый член может включать или выключать другой экспоненциально малый член.

На антистоксовой кривой субдоминантный экспоненциально малый член может переключиться на доминирующий экспоненциально большой член или наоборот.

Такое изменение поведения вдоль стоксовых и антистоксовых кривых напрямую связано с расходимостью асимптотического разложения. Обычный тип дивергенции, наблюдаемый в асимптотическом ряду, который демонстрирует явление Стокса, известен как факториальная дивергенция и имеет типичную форму

$\sum _{j}^{\infty }\epsilon ^{j}{\frac {A\Gamma (j+\alpha )}{\chi ^{j+\alpha }}},$

Где $A$ это функция, известная как префактор, $\chi$ это функция, известная как сингулянт и $\Gamma$ это гамма-функция.

Кривые Стокса определяются по условию $\Im \{\chi \}=0$ и $\Re \{\chi \}>0$. Антистоксова кривая определяется условием $\Re \{\chi \}=0$.

Пример: функция Эйри

Функция Эйри Ai( x ) является одним из двух решений простого дифференциального уравнения

$y''-xy=0,\,$

который часто бывает полезно аппроксимировать для многих значений x , включая комплексные значения. При больших x заданного аргумента решение можно аппроксимировать линейной комбинацией функций

${\frac {e^{\pm {\frac {2}{3}}x^{3/2}}}{x^{1/4}}}.$

Однако линейная комбинация должна меняться по мере того, как аргумент x принимает определенные значения (когда x пересекает разрез ветки ), поскольку эти приближения содержат многозначные функции. Напротив, функция Эйри является однозначной и действительно полной , и поэтому, чтобы понять смысл аппроксимации, нужно выбрать одно значение из нескольких возможных значений (это подразумевает сокращение ветвления для аппроксимации) .Например, если мы считаем предел x большим и реальным и хотим аппроксимировать функцию Эйри как для положительных, так и для отрицательных значений, мы обнаружим, что

График Ai( x ) красным цветом и Bi( x ) синим цветом

${\begin{aligned}\mathrm {Ai} (x)&{}\sim {\frac {e^{-{\frac {2}{3}}x^{3/2}}}{2{\sqrt {\pi }}\,x^{1/4}}}\\\mathrm {Ai} (-x)&{}\sim {\frac {\sin({\frac {2}{3}}x^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,x^{1/4}}}\\\end{aligned}}$

Линии Стокса и антистоксовые линии для функции Эйри.

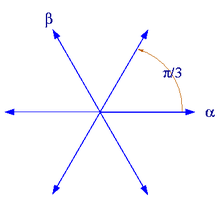
это два совершенно разных выражения. Произошло следующее: когда мы увеличили аргумент x от 0 до pi ( вращая его вокруг верхней полукомплексной плоскости), мы пересекли антистоксову линию, которая в данном случае находится в точке $\operatorname {arg} \,x=\pi /3$. На этой антистоксовой линии коэффициент ${\frac {e^{-{\frac {2}{3}}x^{3/2}}}{x^{1/4}}}$ вынужден прыгать. Коэффициент ${\frac {e^{+{\frac {2}{3}}x^{3/2}}}{x^{1/4}}}$ может перепрыгнуть через эту линию, но не обязан; он может постепенно меняться по мере изменения arg x от π/3 до π, поскольку в этой области он не определен.

Имеются три антистоксовые линии с аргументами π/3, π. –π/3 и три линии Стокса с аргументами 2π/3, 0. –2π/3.

Пример: линейные дифференциальные уравнения второго порядка.

Пример функции Эйри можно обобщить на широкий класс линейных дифференциальных уравнений второго порядка следующим образом. Стандартными заменами переменных уравнение второго порядка часто можно преобразовать к одному из видов

${\frac {d^{2}w}{dz^{2}}}=f(z)w$

где f голоморфна в односвязной области, а w — решение дифференциального уравнения. Тогда в некоторых случаях метод ВКБ дает асимптотическое приближение для w как линейную комбинацию функций вида

${\frac {e^{\pm \int _{a}^{z}{\sqrt {f(z')}}\,dz'}}{f(z)^{1/4}}}$

для некоторой постоянной a . (Выбор различных значений a эквивалентен выбору разных коэффициентов в линейной комбинации.) Антистоксовые линии и линии Стокса тогда являются нулями действительной и мнимой частей соответственно

$\int _{a}^{z}{\sqrt {f(z')}}\,dz'.$

Если a — простой нуль f, то локально f выглядит так: $f'(a)(z-a)$. Решения локально будут вести себя как функции Эйри; у них будет три линии Стокса и три антистоксовые линии, пересекающиеся на точке 0,000 .

См. также

• Суммирование Бореля

Ссылки

• Берри, М.В. (1988), «Феномен Стокса; сглаживание викторианского разрыва». , Инст. Hautes Études Sci. Опубл. Математика. , 68 : 211–221, doi : 10.1007/bf02698550 , MR   1001456 , S2CID   121293430
• Берри, М.В. (1989), "Равномерное асимптотическое сглаживание разрывов Стокса", Proc. Р. Сок. Лонд. A , 422 (1862): 7–21, Bibcode : 1989RSPSA.422....7B , doi : 10.1098/rspa.1989.0018 , JSTOR   2398522 , MR   0990851 , S2CID   122020328
• Мейер, Р.Э. (1989), «Простое объяснение феномена Стокса» , SIAM Rev. , 31 (3): 435–445, doi : 10.1137/1031090 , JSTOR   2031404 , MR   1012299 , заархивировано из оригинала 24 сентября, 2017 год
• Олвер, Фрэнк Уильям Джон (1997) [1974], Асимптотика и специальные функции , AKP Classics, Уэллсли, Массачусетс: AK Peters Ltd., ISBN  978-1-56881-069-0 , МР   1429619
• Стоукс, Г. Г. (1847), «О численном вычислении класса определенных интегралов и бесконечных рядов» , Труды Кембриджского философского общества , IX (I): 166–189.
• Стоукс, Г.Г. (1858), «О разрыве произвольных констант, которые появляются в расходящихся процессах» , Труды Кембриджского философского общества , X (I): 105–128.
• Виттен, Эд (2010). «Аналитическое продолжение теории Черна-Саймонса». arXiv : 1001.2933v4 [ hep-th ].
• Бендер, Карл М .; Орзаг, Стивен А. (1978), Передовые математические методы для ученых и инженеров , Международная серия по чистой и прикладной математике, McGraw Hill Inc., ISBN  0-07-004452-Х
• Абловиц М.Дж. и Фокас А.С. (2003). Комплексные переменные: введение и применение. Издательство Кембриджского университета .