Идеальная поверхность

Идеальная твердая поверхность плоская, жесткая, идеально гладкая, химически однородная и имеет нулевой гистерезис угла смачивания. Нулевой гистерезис означает, что углы контакта при наступлении и отступлении равны.

Рисунок 1. Угол контакта капли жидкости на твердой поверхности.

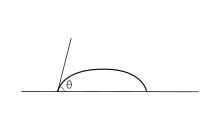
Другими словами, только один термодинамически стабильный контактный угол существует . При помещении капли жидкости на такую ​​поверхность формируется характерный краевой угол, изображенный на рис. 1. Кроме того, на идеальной поверхности капля вернется к исходной форме, если ее нарушить. Следующие выводы применимы только к идеальным твердым поверхностям; они справедливы только для состояния, в котором границы раздела неподвижны и линия границы раздела фаз существует в равновесии.

Рисунок 2: Смачивание различных жидкостей: A показывает жидкость с очень небольшим смачиванием, а C показывает жидкость с большим смачиванием. A имеет большой угол контакта, а C имеет небольшой угол контакта.

Минимизация энергии, три этапа

Рисунок 3: Сосуществование трех жидких фаз во взаимном контакте: α, β и θ представляют собой как метки фаз, так и углы контакта.

Рисунок 4: Треугольник Неймана, связывающий поверхностные энергии и углы смачивания трех жидких фаз, сосуществующих в статическом равновесии, как показано на рисунке 3.

На рисунке 3 показана линия контакта трех фаз. В состоянии равновесия чистая сила на единицу длины, действующая вдоль линии границы между тремя фазами, должна быть равна нулю. Компоненты чистой силы в направлении вдоль каждого из интерфейсов определяются как:

$\gamma _{\alpha \theta }+\gamma _{\theta \beta }\cos {\theta }+\gamma _{\alpha \beta }\cos {\alpha }\ =0$

$\gamma _{\alpha \theta }\cos {\theta }+\gamma _{\theta \beta }+\gamma _{\alpha \beta }\cos {\beta }\ =0$

$\gamma _{\alpha \theta }\cos {\alpha }+\gamma _{\theta \beta }\cos {\beta }+\gamma _{\alpha \beta }\ =0$

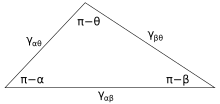
где α, β и θ — показанные углы, а γ _ij — поверхностная энергия между двумя указанными фазами. Эти отношения также могут быть выражены аналогом треугольника, известного как треугольник Неймана, показанного на рисунке 4. Треугольник Неймана согласуется с геометрическим ограничением, согласно которому $\alpha +\beta +\theta =2\pi$и применение к нему закона синусов и закона косинусов дает соотношения, описывающие, как межфазные углы зависят от соотношения поверхностных энергий.

Поскольку эти три поверхностные энергии образуют стороны треугольника , они ограничены неравенствами треугольника: γ _ij < γ _jk + γ _ik, что означает, что ни одно из поверхностных натяжений не может превышать сумму двух других. Если три жидкости с поверхностной энергией, которая не соответствует этим неравенствам, будут приведены в контакт, не будет существовать равновесной конфигурации, соответствующей рисунку 3.

Упрощение до плоской геометрии, соотношение Юнга

Если β-фазу заменить плоской жесткой поверхностью, как показано на рисунке 5, тогда β = π, и второе уравнение суммарной силы упрощается до уравнения Юнга:

Рисунок 5. Угол контакта капли жидкости, смоченной твердой твердой поверхностью.

$\gamma _{SG}\ =\gamma _{SL}+\gamma _{LG}\cos {\theta }$

который связывает поверхностное натяжение между тремя фазами: твердой , жидкой и газообразной . Впоследствии это позволяет предсказать угол контакта капли жидкости с твердой поверхностью на основе знания трех задействованных поверхностных энергий. Это уравнение также применимо, если «газовая» фаза представляет собой другую жидкость, несмешивающуюся с каплей первой «жидкой» фазы.

Реальные гладкие поверхности и контактный угол Юнга

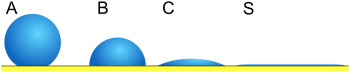
Уравнение Юнга предполагает идеально плоскую и жесткую поверхность. Во многих случаях поверхности далеки от этой идеальной ситуации, и здесь рассматриваются два случая: случай шероховатых поверхностей и случай гладких поверхностей, которые еще являются реальными (конечно жесткими). Даже на идеально гладкой поверхности капля будет принимать широкий спектр углов смачивания: от так называемого опережающего угла смачивания до $\theta _{\mathrm {A} }$, к так называемому углу смачивания, $\theta _{\mathrm {R} }$. Равновесный контактный угол ( $\theta _{\mathrm {c} }$) можно вычислить по формуле $\theta _{\mathrm {A} }$ и $\theta _{\mathrm {R} }$ как показал Тадмор как,

$\theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos {\theta _{\mathrm {A} }}+r_{\mathrm {R} }\cos {\theta _{\mathrm {R} }}}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)$

где

$r_{\mathrm {A} }=\left({\frac {\sin ^{3}{\theta _{\mathrm {A} }}}{2-3\cos {\theta _{\mathrm {A} }}+\cos ^{3}{\theta _{\mathrm {A} }}}}\right)^{1/3}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}{\theta _{\mathrm {R} }}}{2-3\cos {\theta _{\mathrm {R} }}+\cos ^{3}{\theta _{\mathrm {R} }}}}\right)^{1/3}$

Уравнение Юнга – Дюпре и коэффициент расширения.

Уравнение Янга-Дюпре (Томас Янг 1805, Льюис Дюпре 1855) требует, чтобы ни γ _SG, ни γ _SL не могли быть больше суммы двух других поверхностных энергий. Следствием этого ограничения является предсказание полного смачивания , когда γ _SG > γ _SL + γ _LG , и нулевого смачивания, когда γ _SL > γ _SG + γ _LG . Отсутствие решения уравнения Янга – Дюпре является показателем того, что для этих ситуаций не существует равновесной конфигурации с углом контакта от 0 до 180 °.

Полезным параметром для измерения смачивания является параметр растекания S ,

$S\ =\gamma _{SG}-(\gamma _{SL}+\gamma _{LG})$

При S > 0 жидкость полностью смачивает поверхность (полное смачивание). При S < 0 происходит частичное смачивание.

Объединение определения параметра расширения с соотношением Юнга дает уравнение Янга – Дюпре:

$S\ =\gamma _{LG}(\cos \theta -1)$

который имеет физические решения для θ только тогда, когда S <0.

См. также

• Угол контакта
• гистерезис
• Смачивание
• Шероховатость поверхности

Внешние ссылки

• Влияние шероховатости поверхности на угол контакта