Полином Уилкинсона

График полинома Уилкинсона

Сюжет

\operatorname {sgn}(w(x))\ln(1+|w(x)|)

В численном анализе полином Уилкинсона представляет собой особый полином , который был использован Джеймсом Х. Уилкинсоном в 1963 году, чтобы проиллюстрировать трудность поиска корня многочлена: расположение корней может быть очень чувствительным к возмущениям коэффициентов многочлена.

Полином $w(x)=\prod _{i=1}^{20}(x-i)=(x-1)(x-2)\cdots (x-20).$ Иногда термин «полином Уилкинсона» также используется для обозначения некоторых других полиномов, фигурирующих в обсуждении Уилкинсона.

Фон

Полином Уилкинсона возник при исследовании алгоритмов поиска корней многочлена. $p(x)=\sum _{i=0}^{n}c_{i}x^{i}.$ В численном анализе естественным является вопрос, является ли задача нахождения корней $p$ из коэффициентов $c i$ хорошо обусловленной . То есть мы надеемся, что небольшое изменение коэффициентов приведет к небольшому изменению корней. К сожалению, здесь это не тот случай.

Задача является плохо обусловленной, если многочлен имеет кратный корень. Например, полином $x 2$ имеет двойной корень в точке $x = 0$ . Однако полином $x 2 - ε$ (возмущение размера ε ) имеет корни в точке $\pm\sqrt ε$ , что намного больше, чем $ε,$ когда $ε$ мало.

Поэтому естественно ожидать, что плохая обусловленность также возникает, когда полином имеет очень близкие нули. Однако проблема также может быть крайне плохо обусловлена для многочленов с хорошо разделенными нулями. Уилкинсон использовал полином $w (x),$ чтобы проиллюстрировать эту точку зрения (Wilkinson 1963).

В 1984 году он описал личное влияние этого открытия:

Говоря за себя, я считаю это самым травмирующим опытом в моей карьере численного аналитика. ^{[ 1 ]}

Полином Уилкинсона часто используется для иллюстрации нежелательности наивного вычисления собственных значений матрицы путем сначала вычисления коэффициентов характеристического полинома матрицы , а затем нахождения ее корней, поскольку использование коэффициентов в качестве промежуточного шага может привести к крайне плохой обусловленности, даже если исходная проблема была хорошо обусловлена. ^{[ 2 ]}

Обусловливание полинома Уилкинсона

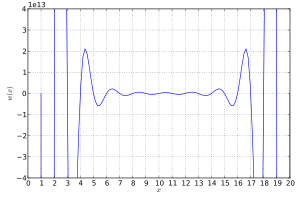
Полином Уилкинсона $w(x)=\prod _{i=1}^{20}(x-i)=(x-1)(x-2)\cdots (x-20)$ явно имеет 20 корней, расположенных в точках $x = 1, 2, ..., 20$ . Эти корни находятся далеко друг от друга. Однако полином все еще очень плохо обусловлен.

Разлагая полином, находим ${\begin{aligned}w(x)={}&x^{20}-210x^{19}+20615x^{18}-1256850x^{17}+53327946x^{16}\\&{}-1672280820x^{15}+40171771630x^{14}-756111184500x^{13}\\&{}+11310276995381x^{12}-135585182899530x^{11}\\&{}+1307535010540395x^{10}-10142299865511450x^{9}\\&{}+63030812099294896x^{8}-311333643161390640x^{7}\\&{}+1206647803780373360x^{6}-3599979517947607200x^{5}\\&{}+8037811822645051776x^{4}-12870931245150988800x^{3}\\&{}+13803759753640704000x^{2}-8752948036761600000x\\&{}+2432902008176640000.\end{aligned}}$

Если коэффициент при x ¹⁹ уменьшается с −210 на 2 ⁻²³ до −210,0000001192, то значение полинома w (20) уменьшается от 0 до −2 ⁻²³20 ¹⁹ = −6.25×10 ¹⁷, а корень при $x = 20$ вырастает до $x \approx 20,8$ . Корни при $x = 18$ и $x = 19$ сталкиваются в двойной корень при $x \approx 18,62$ превращается в пару комплексно-сопряженных корней при $x \approx 19,5 \pm 1,9 i$ , который при дальнейшем увеличении возмущения . 20 корней становятся (до 5 десятичных знаков) ${\begin{array}{rrrrr}1.00000&2.00000&3.00000&4.00000&5.00000\\[8pt]6.00001&6.99970&8.00727&8.91725&20.84691\\[8pt]10.09527\pm {}&11.79363\pm {}&13.99236\pm {}&16.73074\pm {}&19.50244\pm {}\\[-3pt]0.64350i&1.65233i&2.51883i&2.81262i&1.94033i\end{array}}$

Некоторые корни сильно смещены, хотя изменение коэффициента незначительно, а первоначальные корни кажутся широко расставленными. Уилкинсон с помощью анализа устойчивости, обсуждаемого в следующем разделе, показал, что такое поведение связано с тем фактом, что некоторые корни α (например, α = 15) имеют множество корней β , которые «близки» в том смысле, что | α − β | меньше, чем | α |.

Уилкинсон выбрал возмущение 2 ⁻²³ потому что его Pilot ACE компьютер с плавающей запятой имел 30-битные числа , поэтому для чисел около 210, 2 ⁻²³ произошла ошибка в позиции первого бита, не представленная в компьютере. Два действительных числа: −210 и −210 − 2. ⁻²³, представлены одним и тем же числом с плавающей запятой, что означает, что 2 ⁻²³ — это неизбежная ошибка при представлении реального коэффициента, близкого к -210, числом с плавающей запятой на этом компьютере. Анализ возмущений показывает, что 30-битная точность коэффициентов недостаточна для разделения корней полинома Уилкинсона.

Анализ стабильности

Предположим, что мы возмущаем полином $p (x) = Π (x - α j)$ с корнями $αj,$ добавив небольшое кратное $t \cdot c (x)$ к многочлену $c (x)$ как это влияет на корни $αj .$ , и спросите , В первом порядке изменение корней будет контролироваться производной ${d\alpha _{j} \over dt}=-{c(\alpha _{j}) \over p^{\prime }(\alpha _{j})}.$ Когда производная велика, корни будут более устойчивы при изменении $t$ , и наоборот, если эта производная мала, корни будут неустойчивы. В частности, если $α j$ — кратный корень, то знаменатель обращается в нуль. В этом случае α _j обычно не дифференцируема по $t$ (если только $c$ там не обращается в нуль), и корни будут крайне неустойчивы.

Для малых значений $t$ возмущенный корень определяется разложением в степенной ряд по $t$ $\alpha _{j}+{d\alpha _{j} \over dt}t+{d^{2}\alpha _{j} \over dt^{2}}{t^{2} \over 2!}+\cdots$ и можно ожидать проблем, когда | т | больше радиуса сходимости этого степенного ряда, который определяется наименьшим значением | т | что корень $αj такой ,$ становится кратным. Очень грубая оценка этого радиуса берет половину расстояния от $α j$ до ближайшего корня и делится на производную, указанную выше.

В примере полинома Уилкинсона степени 20 корни заданы как $α j = j$ для $j = 1, ..., 20$ , а $c (x)$ равно x ¹⁹. Таким образом, производная определяется выражением ${d\alpha _{j} \over dt}=-{\alpha _{j}^{19} \over \prod _{k\neq j}(\alpha _{j}-\alpha _{k})}=-\prod _{k\neq j}{\alpha _{j} \over \alpha _{j}-\alpha _{k}}.\,\!$ Это показывает, что корень $α j$ будет менее устойчивым, если корней много. $α k$ близок к $α j$ в том смысле, что расстояние |α _j − α _k | между ними меньше |α _j |.

Пример . Для корня α ₁ = 1 производная равна 1/19! что очень мало; этот корень устойчив даже при больших изменениях t . Это потому, что все остальные корни β находятся далеко от него, в том смысле, что | α ₁ − β | = 1, 2, 3, ..., 19 больше, чем | α ₁ | = 1. Например, даже если t достигает –10000000000, корень α ₁ изменяется только от 1 примерно до 0,99999991779380 (что очень близко к аппроксимации первого порядка 1 + t /19! ≈ 0,99999991779365). Точно так же другие малые корни полинома Уилкинсона нечувствительны к изменениям t .

Пример . С другой стороны, для корня α ₂₀ = 20 производная равна −20 ¹⁹/19! который огромен (около 43000000), поэтому этот корень очень чувствителен к небольшим изменениям t . Остальные корни β близки к α ₂₀ в том смысле, что | β − α ₂₀ | = 1, 2, 3, ..., 19 меньше | α ₂₀ | = 20. При t = −2 ^− 23 первое приближение 20 − t ·20 ¹⁹/19! = 25,137... к возмущенному корню 20,84... ужасно; это еще более очевидно для корня α ₁₉ , где возмущенный корень имеет большую мнимую часть, но приближение первого порядка (и в этом отношении все приближения более высокого порядка) вещественны. Причина этого несоответствия в том, что | т | ≈ 0,000000119 больше радиуса сходимости упомянутого выше степенного ряда (который составляет около 0,0000000029, что несколько меньше значения 0,00000001, данного грубой оценкой), поэтому линеаризованная теория неприменима. Для такого значения, как t = 0,000000001, которое значительно меньше этого радиуса сходимости, аппроксимация первого порядка 19,9569... достаточно близка к корню 19,9509...

На первый взгляд корни α ₁ = 1 и α ₂₀ = 20 многочлена Уилкинсона кажутся одинаковыми, так как они находятся на противоположных концах симметричной прямой корней и имеют одинаковый набор расстояний 1, 2, 3,... ., 19 от других корней. Однако приведенный выше анализ показывает, что это грубое заблуждение: корень α ₂₀ = 20 менее устойчив, чем α ₁ = 1 (к небольшим возмущениям коэффициента при x ¹⁹) в 20 раз ¹⁹ = 5242880000000000000000000.

Второй пример Уилкинсона

Второй пример, рассмотренный Уилкинсоном: $w_{2}(x)=\prod _{i=1}^{20}(x-2^{-i})=(x-2^{-1})(x-2^{-2})\cdots (x-2^{-20}).$ Двадцать нулей этого многочлена находятся в геометрической прогрессии с общим отношением 2, и, следовательно, частное $\alpha _{j} \over \alpha _{j}-\alpha _{k}$ не может быть большим. Действительно, нули $w 2$ вполне устойчивы к большим относительным изменениям коэффициентов.

Эффект от основы

Расширение $p(x)=\sum _{i=0}^{n}c_{i}x^{i}$ выражает полином в определенном базисе, а именно в базисе мономов. Если многочлен выразить в другом базисе, то задача нахождения его корней может перестать быть плохо обусловленной. Например, в форме Лагранжа небольшое изменение одного (или нескольких) коэффициентов не должно слишком сильно менять корни. Действительно, базисные полиномы для интерполяции в точках 0, 1, 2, ..., 20 равны $\ell _{k}(x)=\prod _{i=0,\ldots ,20 \atop i\neq k}{\frac {x-i}{k-i}},\qquad {\text{for}}\quad k=0,\ldots ,20.$

Любой полином (степени 20 или меньше) можно выразить в этом базисе: $p(x)=\sum _{i=0}^{20}d_{i}\ell _{i}(x).$

Для полинома Уилкинсона находим $w(x)=(20!)\ell _{0}(x)=\sum _{i=0}^{20}d_{i}\ell _{i}(x)\quad {\text{with}}\quad d_{0}=(20!),\,d_{1}=d_{2}=\cdots =d_{20}=0.$

Учитывая определение базисного полинома Лагранжа $ℓ 0 (x)$ , изменение коэффициента $d 0$ не приведет к изменению корней $w$ . Однако изменение остальных коэффициентов (все они равны нулю) несколько изменит корни. Следовательно, полином Уилкинсона хорошо обусловлен в этом базисе.

Примечания

^ Уилкинсон, Джеймс Х. (1984). «Коварный полином». В Джине Х. Голубе (ред.). Исследования в области численного анализа . Математическая ассоциация Америки. п. 3. ISBN 978-0-88385-126-5 .
^ Трефетен, Ллойд Н.; Бау, Дэвид (1997), Численная линейная алгебра , SIAM

Ссылки

Уилкинсон обсуждал «свой» полином в

Дж. Х. Уилкинсон (1959). Оценка нулей плохо обусловленных многочленов. Часть I. Numerische Mathematik 1 : 150–166.
Дж. Х. Уилкинсон (1963). Ошибки округления в алгебраических процессах . Энглвуд Клиффс, Нью-Джерси: Прентис Холл.

Он упоминается в стандартных учебниках по численному анализу, например

Ф.С. Актон, Работающие численные методы , ISBN 978-0-88385-450-1 , с. 201.

Другие ссылки:

Рональд Г. Мозье (июль 1986 г.). Корневые окрестности многочлена. Математика вычислений 47 (175): 265–273.
Дж. Х. Уилкинсон (1984). Коварный полином. Исследования по численному анализу , под ред. Голуба Г.Х., стр. 1–28. (Этюды по математике, т. 24). Вашингтон, округ Колумбия: Математическая ассоциация Америки.

Высокоточный численный расчет представлен в:

Рэй Бювель, Полиномы и рациональные функции , часть Руководства пользователя калькулятора RPN (для Python), получено 29 июля 2006 г.

[1] Уилкинсон, Джеймс Х. (1984). «Коварный полином». В Джине Х. Голубе (ред.). Исследования в области численного анализа . Математическая ассоциация Америки. п. 3. ISBN 978-0-88385-126-5 .

[TrefethenBau-2] Трефетен, Ллойд Н.; Бау, Дэвид (1997), Численная линейная алгебра , SIAM

[ 1 ]

[ 2 ]