Уравнение Стритера – Фелпса


Уравнение Стритера-Фелпса используется при изучении загрязнения воды в качестве инструмента моделирования качества воды . Модель описывает, как растворенный кислород (РК) уменьшается в реке или ручье на определенном расстоянии за счет снижения биохимической потребности в кислороде (БПК). Уравнение было выведено Х. У. Стритером, санитарным инженером, и Эрлом Б. Фелпсом , консультантом Службы общественного здравоохранения США , в 1925 году на основе полевых данных по реке Огайо . Уравнение также известно как уравнение провисания DO.
Уравнение Стритера – Фелпса
[ редактировать ]Уравнение Стритера-Фелпса определяет связь между концентрацией растворенного кислорода и биологической потребностью в кислороде с течением времени и является решением линейного дифференциального уравнения первого порядка. [ 1 ]
Это дифференциальное уравнение утверждает, что общее изменение дефицита кислорода (D) равно разнице между двумя скоростями дезоксигенации и реаэрации в любой момент времени.
Уравнение Стритера-Фелпса, предполагающее, что поток поршневого потока в установившемся состоянии будет тогда

где
- - дефицит насыщения, который можно получить из концентрации растворенного кислорода при насыщении минус фактическая концентрация растворенного кислорода ( ). имеет размеры .
- - скорость дезоксигенации , обычно в .
- - скорость реаэрации, обычно в .
- — это начальная потребность органических веществ в воде в кислороде, также называемая предельным БПК (БПК в момент времени t=бесконечность). Единица является .
- - потребность в кислороде, оставшаяся в момент времени t, .
- это начальный дефицит кислорода .
- это прошедшее время, обычно .
обычно лежит в пределах 0,05-0,5 и обычно лежит в пределах 0,4-1,5 . [ 2 ]
Уравнение Стритера-Фелпса также известно как уравнение прогиба DO. Это связано с формой графика изменения ДО во времени.

Критический дефицит кислорода
[ редактировать ]На кривой падения растворенного кислорода минимальная концентрация возникает в некоторой точке вдоль потока. Если уравнение Стритера-Фелпса дифференцировать по времени и приравнять к нулю, время, в которое происходит минимальный DO, выражается выражением
Чтобы найти величину критического дефицита кислорода, , уравнение Стритера – Фелпса объединяется с приведенным выше уравнением для критического времени . Тогда минимальная концентрация растворенного кислорода равна
Математически можно получить отрицательное значение , хотя на самом деле невозможно иметь отрицательное количество DO. [ 3 ]
Расстояние, пройденное по реке от данной точки, источника загрязнения или сброса отходов вниз по течению до реки. (что является минимальным DO) находится по формуле
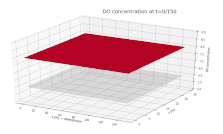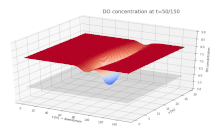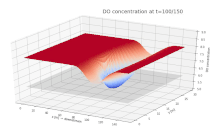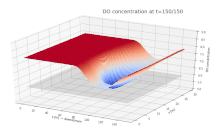
График поверхности, показывающий концентрацию растворенного кислорода (DO) в реке. DO показан на вертикальной оси, а направления вдоль и поперек потока - на осях x и y соответственно. Непрерывный ввод биологического материала добавляется в реку при x = 75 м, y = 15 м, начиная с t = 0.
где - скорость течения потока. Эта формула является хорошим приближением, если поток можно рассматривать как поршневой (турбулентный).
Оценка скорости реаэрации
[ редактировать ]Существует несколько оценок скорости реаэрации, которые обычно следуют уравнению
где
- является константой.
- — скорость потока [м/с].
- — глубина [м].
- является константой.
- является константой.
Константы зависят от системы, к которой применяется уравнение, т.е. скорости потока и размера ручья или реки. В литературе встречаются разные значения.
Программное обеспечение « Международная гидрологическая программа » применяет следующее уравнение, полученное на основе значений, используемых в опубликованной литературе. [ 4 ]
где
- .
- — средняя скорость потока [м/с].
- — средняя глубина течения реки [м].
Температурная коррекция
[ редактировать ]Как скорость дезоксигенации, так и и скорость реаэрации, можно скорректировать по температуре, следуя общей формуле. [ 2 ]
где
- это норма при 20 градусах Цельсия.
- θ — константа, которая различается для двух скоростей.
- — фактическая температура в потоке в градусах Цельсия.
Обычно θ имеет значение 1,048 для и 1,024 для . Повышение температуры оказывает наибольшее влияние на скорость деоксигенации и приводит к увеличению критического дефицита ( ), и уменьшается. Кроме того, снижение концентрация происходит с повышением температуры, что приводит к уменьшению концентрации DO. [ 2 ]
Смешение рек
[ редактировать ]Когда два ручья или реки сливаются или вода сбрасывается в ручей, можно определить БПК и РК после смешивания, предполагая установившиеся условия и мгновенное смешивание. Два потока считаются разбавлением друг друга, поэтому начальные значения БПК и растворенного кислорода будут равны. [ 4 ]
и
где
- — начальная концентрация БПК в реке после места смешивания, также называемая БПК(0). Единица является .
- – фоновый БПК концентрации в реке .
- – БПК содержимого сливающейся реки .
- — начальная концентрация растворенного кислорода в реке ниже места слияния. .
- – фоновая концентрация содержания растворенного кислорода в реке .
- – фоновая концентрация содержания растворенного кислорода в сливающейся реке .
- — расход реки вверх по течению от места смешения .
- — расход сливающейся реки вверх по течению от точки смешения .
Численный подход
[ редактировать ]В настоящее время классическое уравнение Стритера-Фелпса можно решить численно с помощью компьютеров. Дифференциальные уравнения решаются путем интегрирования.
История
[ редактировать ]опубликовали исследование явлений окисления и реаэрации в реке Огайо В 1925 году санинженер Гарольд Уорнер Стритер и консультант Эрл Бернард Фелпс (1876–1953) в США. Исследование было основано на данных, полученных с мая 1914 года по апрель 1915 года Службой общественного здравоохранения США под руководством Сурга. WH Мороз. [ 1 ]
Более сложные версии модели Стритера-Фелпса были представлены в 1960-х годах, когда компьютеры позволили учесть дальнейший вклад в выделение кислорода в потоках. Во главе этого развития стояли О'Коннор (1960) и Томанн (1963). [ 5 ] О'Коннор добавил вклад фотосинтеза, дыхания и потребности отложений в кислороде (СОД). [ 6 ] Томанн расширил модель Стритера-Фелпса, включив в нее многосегментные системы. [ 7 ]
Приложения и ограничения
[ редактировать ]Простая модель Стритера-Фелпса основана на предположении, что один входной поток БПК распределяется равномерно в поперечном сечении ручья или реки и что он движется как пробковый поток без смешивания в реке. [ 8 ] Более того, в классической модели Стритера-Фелпса рассматривается только один поглотитель РК (углеродистый БПК) и один источник РК (реаэрация). [ 9 ] Эти упрощения приведут к ошибкам в модели. Например, модель не включает удаление БПК путем седиментации, что взвешенный БПК преобразуется в растворенное состояние, что осадкам требуется кислород и что фотосинтез и дыхание будут влиять на кислородный баланс. [ 8 ]
Расширенная модель
[ редактировать ]Помимо окисления органического вещества и процесса реаэрации, в потоке происходит множество других процессов, влияющих на РК. [ 8 ] Чтобы создать более точную модель, можно включить эти факторы, используя расширенную модель.
Расширенная модель является модификацией традиционной модели и включает внутренние источники (реаэрацию и фотосинтез) и стоки (БПК, фоновый БПК, СОД и дыхание) РК. Не всегда необходимо включать все эти параметры. Вместо этого соответствующие источники и поглотители можно суммировать, чтобы получить общее решение для конкретной модели. [ 2 ] Параметры расширенной модели могут быть измерены в полевых условиях или оценены теоретически.
Фон БПК
[ редактировать ]Фоновый БПК или потребность бентоса в кислороде является диффузным источником БПК, представленным разложением органического вещества, которое уже осело на дно. Это приведет к постоянному диффузному притоку, поэтому изменение БПК с течением времени будет
где
- — скорость потребления кислорода БПК, обычно в .
- БПК органических веществ в воде .
- это фоновый вход BOD .
Седиментация БПК
[ редактировать ]Осажденный БПК не потребляет кислород напрямую, и поэтому это следует учитывать. Это делается путем введения скорости удаления БПК в сочетании со скоростью потребления кислорода БПК. Определение общей скорости удаления кислорода по БПК. [ 2 ]
где
- — скорость потребления кислорода БПК, обычно в .
- - скорость оседания БПК, обычно в .
Изменение БПК с течением времени описывается как
где БПК органических веществ в воде .
обычно находится в диапазоне 0,5-5 . [ 2 ]
Потребность осадков в кислороде
[ редактировать ]
Кислород может потребляться организмами, живущими в отложениях. Этот процесс называется потребностью осадков в кислороде (СОД). Измерение СОД можно провести путем измерения изменения содержания кислорода в контейнере с отложениями (бентический респирометр).
Изменение дефицита кислорода за счет его потребления осадками описывается как
где
- глубина реки [м]
- это СОД
- D - дефицит насыщения .
- — скорость реаэрации [ ].
Диапазон СОД обычно находится в пределах 0,1 – 1. для естественной реки с низким уровнем загрязнения и 5 – 10 для реки с умеренным и сильным загрязнением. [ 2 ]
Нитрификация
[ редактировать ]Аммоний окисляется до нитрата в аэробных условиях.
- НХ 4 + + 2O2 → NO3 − + Н 2 О + 2Н +
Окисление аммония можно рассматривать как часть БПК, так что БПК = CBOD + NBOD, где CBOD — это углеродсодержащая биохимическая потребность в кислороде , а NBOD — азотистый БПК. Обычно CBOD намного превышает концентрацию аммония, и поэтому NBOD часто не нужно учитывать. Изменение дефицита кислорода вследствие окисления аммония описывается как
где
- D – дефицит насыщения.
- это скорость нитрификации .
- – концентрация аммонийного азота.
Диапазон обычно составляет 0,05-0,5 . [ 2 ]
Фотосинтез и дыхание
[ редактировать ]Фотосинтез и дыхание осуществляют водоросли и макрофиты. Дыхание также осуществляется бактериями и животными. Предполагая устойчивое состояние (среднедневное чистое значение), изменение дефицита будет
где
- это дыхание .
- это фотосинтез .
Обратите внимание, что БПК включает дыхание только микроорганизмов, например, водорослей и бактерий, а не макрофитов и животных.
Из-за изменения освещения во времени изменение фотосинтетического кислорода можно описать периодической функцией во времени, где время находится после восхода солнца и перед заходом солнца. [ 2 ]
где
- фотосинтез в данный момент времени .
- это суточный максимум фотосинтеза .
- это часть дня с солнечным светом, обычно день.
- это время восхода солнца .
Диапазон среднесуточной стоимости первичной продукции обычно составляет 0,5-10 . [ 2 ]
См. также
[ редактировать ]- Загрязнение воды
- Моделирование качества воды
- Биохимическая потребность в кислороде
- Оксигенация (окружающая среда)
- Насыщение кислородом
- Истощение кислорода
- Гипоксия (экологическая)
- Деоксигенация
- Аэрация воды
- Фотосинтез
- Нитрификация
- Законы диффузии Фика
- Река Огайо
- Служба общественного здравоохранения США
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Стритер Х.В., Фелпс Э.Б., 1925 г., Исследование загрязнения и естественной очистки реки Огайо. III. Факторы, связанные с явлениями окисления и реаэрации, Бюллетень общественного здравоохранения №. 146, перепечатано Министерством здравоохранения, образования и социального обеспечения США, Службой общественного здравоохранения, 1958 г., ISBN B001BP4GZI, http://dspace.udel.edu:8080/dspace/bitstream/handle/19716/1590/C%26EE148.pdf? последовательность=2
- ^ Перейти обратно: а б с д и ж г час я дж Шнур Дж., 1996, Моделирование окружающей среды, судьба и перенос загрязнителей в воде, воздухе и почве, Wiley-Interscience, ISBN 978-0-471-12436-8
- ^ Готовцев А.В., 2010, Модификация системы Стритера-Фелпса с целью учета обратной связи между концентрацией растворенного кислорода и скоростью окисления органических веществ, ISSN 0097-8078, Водные ресурсы, Vol. 37, № 2, стр. 245–251. Плеяды Паблишинг, ООО
- ^ Перейти обратно: а б Йоланкай Г., 1997, Базовые модели качества речной воды, Программа компьютерного обучения (CAL) по моделированию качества воды (WQMCAL версия 1.1), Международная гидрологическая программа, Технические документы по гидрологии, № 13
- ^ Рассел К.С., Вон В.Дж., Кларк К.Д., Родригес Д.Д., Дарлинг А.Х., 2001, Инвестиции в качество воды: измерение выгод, затрат и рисков, Межамериканский банк развития, Вашингтон, округ Колумбия
- ^ Лунг WS, 2001, Моделирование качества воды для распределения отходов и TMDL, John Wiley & Sons, Inc.
- ^ Вурбс Р.А., 1994, Компьютерные модели для планирования и управления водными ресурсами, Техасский университет A&M.
- ^ Перейти обратно: а б с Лин С.Д., Ли CC (2001). Руководство по расчетам воды и сточных вод . МакГроу Хилл Профессионал. стр. 13–. ISBN 978-0-07-137195-7 .
- ^ Шнур Дж., 1986, Моделирование окружающей среды, судьба и перенос загрязнителей в воде, воздухе и почве, Wiley-Interscience
Внешние ссылки
[ редактировать ]- О'Коннор DJ, 1960, Кислородный баланс устья , Журнал отдела санитарной техники, ASCE, Vol. 86, № СА3, Учеб. Документ 2472, май 1960 г.
- Шнор Дж. (1996). Экологическое моделирование, судьба и перенос загрязнителей в воде, воздухе и почве . Уайли-Интерсайенс. ISBN 978-0-471-12436-8 .
- Томанн Р.В., 1963, Математическая модель растворенного кислорода , Журнал отдела санитарной техники, Американское общество инженеров-строителей, том 89, № SA5.












![{\displaystyle [{\tfrac {\mathrm {g} {\mathrm {m} ^{3}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a846316b184fac08cedc66c32bd4ceb071ddaae)

![{\displaystyle [d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4f4d84e860f2ffd5b55eec14cfbf735dd01689)
![{\displaystyle t_{crit}={\frac {1}{k_{2}-k_{1}}}\ln {\left[{\frac {k_{2}}{k_{1}}}\left ({1-{\frac {D_{a}(k_{2}-k_{1})}{L_{a}k_{1}}}}\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb0a3829bfc0a64c2d3916fd686ed3761aeb1114)













![{\displaystyle [d^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70f7a7f8b6420c8da2a11bd52e64c99a5c68aef1)













![{\displaystyle [{\tfrac {m^{3}}{s}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1c4d695d346d5825d718a419c5f822231758ed)









![{\displaystyle [{\tfrac {g}{m^{2}d}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7fa46a186240ccb9e63217dddcc2dc3b05404)






![{\displaystyle [{\tfrac {mg}{Ld}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24972a26ea02b83de31e0501a81e20741158ed9b)








