Последовательность Спекера

В теории вычислимости — последовательность Шпкера это вычислимая , монотонно возрастающая , ограниченная последовательность рациональных чисел которой , верхняя грань не является вычислимым действительным числом . Первый пример такой последовательности построил Эрнст Шпекер (1949).

Существование последовательностей Спекера имеет последствия для вычислимого анализа . Тот факт, что такие последовательности существуют, означает, что совокупность всех вычислимых действительных чисел не удовлетворяет принципу наименьшей верхней границы реального анализа, даже если рассматривать только вычислимые последовательности. Обычный способ решить эту трудность — рассматривать только последовательности, сопровождающиеся модулем сходимости ; ни одна последовательность Спеккера не имеет вычислимого модуля сходимости. В более общем смысле, последовательность Спекера называется рекурсивным контрпримером к принципу наименьшей верхней границы, т.е. конструкцией, которая показывает, что эта теорема неверна, когда она ограничена вычислимыми действительными числами.

Принцип наименьшей верхней границы также анализировался в программе обратной математики , где была определена точная сила этого принципа. В терминологии этой программы принцип наименьшей верхней границы эквивалентен ACA ₀ над RCA ₀ . Фактически, доказательство прямой импликации, т.е. того, что из принципа наименьшей верхней границы следует ACA ₀ , легко получить из учебника (см. Simpson, 1999) невычислимости супремума в принципе наименьшей верхней границы.

Строительство [ править ]

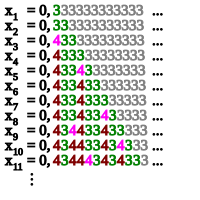
Следующая конструкция описана Кушнером (1984). Пусть A — любое рекурсивно перечислимое множество натуральных чисел , которое неразрешимо , и пусть ( a _i ) — вычислимое перечисление A без повторения. Определим последовательность ( q _n ) рациональных чисел по правилу

q_{n}=\sum _{i=0}^{n}2^{-a_{i}-1}.

Ясно, что каждое неотрицательно _qn и рационально и что последовательность строго _qn возрастает. Более того, поскольку a _i не имеет повторений, можно оценить каждое q _n по ряду

\sum _{i=0}^{\infty }2^{-i-1}=1.

Таким образом, последовательность ( qn _имеет ) ограничена сверху единицей. Классически это означает, что верхнюю _qn грань x .

Показано, что x не является вычислимым действительным числом. В доказательстве используется особый факт о вычислимых действительных числах. Если бы x было вычислимо, то существовала бы вычислимая функция r ( n ) такая, что | q _j - q _я | < 1/ n для всех i , j > r ( n ). Чтобы вычислить r , сравните двоичное разложение x с двоичным разложением q _i для все больших и больших значений i . Определение q _i приводит к тому, что одна двоичная цифра меняется от 0 до 1 каждый раз, когда i увеличивается на 1. Таким образом, будет некоторое n , где достаточно большой начальный сегмент x уже определен q _n, и в нем не будет никаких дополнительных двоичных цифр. этот сегмент когда-либо может быть включен, что приводит к оценке расстояния между q _i и q _j для i , j > n .

Если бы любая такая функция r была вычислимой, это привело бы к следующей процедуре решения для A . Учитывая входные данные k , вычислите r (2 ^{к +1}). Если бы k появился в последовательности ( a _i последовательности ( q _{i ) на 2} ), это привело бы к увеличению ^{− к -1}, но этого не может произойти, если все элементы ( q _i ) находятся в пределах 2 ^{− к -1} друг друга. Таким образом, если k будет перечислено в a _i , оно должно быть пронумеровано для значения i меньше r (2 ^{к +1}). Это оставляет конечное число возможных мест, где k можно пронумеровать . Чтобы завершить процедуру принятия решения, проверьте их эффективным образом, а затем верните 0 или 1 в зависимости от того, ли k найден .

См. также [ править ]

Вычисление в пределе

Ссылки [ править ]

Дуглас Бриджес и Фред Ричман. Разновидности конструктивной математики, Оксфорд, 1987.
Б. А. Кушнер (1984), Лекции по конструктивному математическому анализу , Американское математическое общество, Переводы математических монографий, т. 60.
Якоб Г. Симонсен (2005), «Возвращение к последовательностям Спеккера», Mathematical Logic Quarterly , т. 51, стр. 532–540. дои : 10.1002/malq.200410048
С. Симпсон (1999), Подсистемы арифметики второго порядка , Springer.
Э. Спекер (1949), «Неконструктивно доказуемые положения анализа» Журнал символической логики , т. 14, стр. 145–158.