Угловая трансферная матрица

В статистической механике угловая матрица переноса описывает эффект добавления квадранта к решетке. Представленный Родни Бакстером в 1968 году как расширение построчной матрицы Крамерса-Ваннье, он обеспечивает мощный метод изучения решетчатых моделей . Расчеты с использованием угловых трансфер-матриц привели Бакстера к точному решению модели твердого шестиугольника в 1980 году.

Определение

Рассмотрим модель IRF (взаимодействие вокруг грани), т. е. модель квадратной решетки со спином σ _i, присвоенным каждому узлу i, и взаимодействиями, ограниченными вращениями вокруг общей грани. Пусть полная энергия определяется выражением

$E=\sum _{all \atop faces}\epsilon \left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right),$

где для каждой грани окружающие точки i , j , k и l расположены следующим образом:

Для решетки с N узлами статистическая сумма равна

$Z_{N}=\sum _{all \atop spins}\prod _{all \atop faces}w\left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right),$

где сумма ведется по всем возможным конфигурациям спина, а w — вес Больцмана.

$w\left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right)=\exp \left(-\epsilon \left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right)/k_{B}T\right).$

Для упрощения обозначений мы используем ферромагнитную решетку типа Изинга , где каждый спин имеет значение +1 или -1, а основное состояние задается всеми спинами вверх (т.е. полная энергия минимизируется, когда все спины решетки имеют значение +1). Мы также предполагаем, что решетка обладает 4-кратной вращательной симметрией (с точностью до граничных условий) и инвариантна к отражению. Эти упрощающие предположения не имеют решающего значения, и распространение определения на общий случай относительно просто.

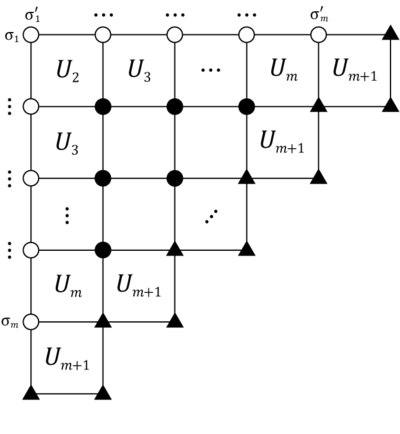
Теперь рассмотрим квадрант решетки, показанный ниже:

Внешним граничным узлам, отмеченным треугольниками, присваиваются спины основного состояния (в данном случае +1). Участки, отмеченные светлыми кружками, образуют внутренние границы квадранта; с ними наборы спинов обозначены {σ1 _, ...,σm _} и {σ'1 _, ...,σ'm _} , где σ1 ₌ σ'1 _{связанные} . Есть 2 ^м возможные конфигурации для каждой внутренней границы, поэтому мы определяем 2 ^м ×2 ^м матрица по входу на

$A_{\sigma |\sigma '}=\delta \left(\sigma _{1},\sigma _{1}'\right)\sum _{interior \atop spins}\prod _{all \atop faces}w\left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right).$

Таким образом, матрица A является угловой матрицей переноса для данного квадранта решетки. Поскольку внешние граничные спины фиксированы и сумма ведется по всем внутренним граничным спинам, каждая запись A является функцией внутренних граничных спинов. Дельта Кронекера в выражении гарантирует, что σ ₁ = σ' ₁ , поэтому, упорядочив конфигурации соответствующим образом, мы можем представить A как блочную диагональную матрицу:

${\begin{array}{cccc}&&{\begin{array}{ccccc}\sigma _{1}'=+1&&&&\sigma _{1}'=-1\end{array}}\\A&=&\left[{\begin{array}{ccccccc}&&&|\\&A_{+}&&|&&0\\&&&|\\-&-&-&|&-&-&-\\&&&|\\&0&&|&&A_{-}\\&&&|\end{array}}\right]&{\begin{array}{c}\sigma _{1}=+1\\\\\\\\\sigma _{1}=-1\end{array}}\end{array}}$

Угловые передаточные матрицы связаны со статистической суммой простым образом. В нашем упрощенном примере мы строим полную решетку из четырех повернутых копий квадранта решетки, где внутренние граничные наборы спинов σ, σ', σ" и σ'" могут различаться:

Статистическая сумма тогда записывается через угловую передаточную матрицу A как

$Z_{N}=\sum _{\sigma ,\sigma ',\sigma '',\sigma '''}A_{\sigma |\sigma '}A_{\sigma '|\sigma ''}A_{\sigma ''|\sigma '''}A_{\sigma '''|\sigma }={\textrm {tr}}A^{4}.$

Обсуждение

Отношение рекурсии

Угловая трансферная матрица A _{2 ^м} (определенная для квадранта m × m ) может быть выражена через меньшие угловые матрицы переноса A _{2 ^{м -1}} и А _{2 ^{м -2}} (определено для уменьшенных ( m -1)×( m -1) и ( m -2)×( m -2) квадрантов соответственно). Это рекурсивное соотношение позволяет, в принципе, итеративно вычислить угловую матрицу переноса для любого квадранта решетки конечного размера.

Как и их аналоги из строки в строку, матрицы переноса углов могут быть включены в матрицы переноса граней, которые соответствуют добавлению одной грани в решетку. Для квадранта решетки, приведенного ранее, матрицы переноса граней имеют размер 2 ^м ×2 ^м и определяется по входу

$\left(U_{i}\right)_{\sigma |\sigma '}=\delta \left(\sigma _{1},\sigma _{1}'\right)\cdots \delta \left(\sigma _{i-1},\sigma _{i-1}'\right)w\left(\sigma _{i},\sigma _{i+1},\sigma _{i}',\sigma _{i-1}\right)\delta \left(\sigma _{i+1},\sigma _{i+1}'\right)\cdots \delta \left(\sigma _{m},\sigma _{m}'\right),$

где 2 ≤ i ≤ m +1. В частности, вблизи внешней границы мы имеем

$\left(U_{m}\right)_{\sigma |\sigma '}=\delta \left(\sigma _{1},\sigma _{1}'\right)\cdots \delta \left(\sigma _{m-1},\sigma _{m-1}'\right)w\left(\sigma _{m},+1,\sigma _{m}',\sigma _{m-1}\right),$

$\left(U_{m+1}\right)_{\sigma |\sigma '}=\delta \left(\sigma _{1},\sigma _{1}'\right)\cdots \delta \left(\sigma _{m},\sigma _{m}'\right)w\left(+1,+1,+1,\sigma _{m}\right).$

Таким образом, матрица углового переноса A факторизуется как

$A=F_{2}\cdots F_{m+1},$

где

$F_{j}=U_{m+1}\cdots U_{j}.$

Графически это соответствует:

Нам также нужны 2 ^м ×2 ^м матрицы A * и A **, определяемые по элементам формулой

$\left(A^{*}\right)_{\sigma |\sigma '}=\delta \left(\sigma _{1},\sigma _{1}'\right)A_{\sigma _{2},\ldots ,\sigma _{m}|\sigma _{2}',\ldots ,\sigma _{m}'},$

$\left(A^{**}\right)_{\sigma |\sigma '}=\delta \left(\sigma _{1},\sigma _{1}'\right)\delta \left(\sigma _{2},\sigma _{2}'\right)A_{\sigma _{3},\ldots ,\sigma _{m}|\sigma _{3}',\ldots ,\sigma _{m}'},$

где матрицы A , записи которых появляются в правой части, имеют размер 2 ^{м -1} ×2 ^{м -1} и 2 ^{м -2} ×2 ^{м -2} соответственно. Это более четко написано как

$A^{*}=I_{2}\otimes A_{2^{m-1}}=\left[{\begin{array}{cc}A&0\\0&A\end{array}}\right],$

$A^{**}=I_{2}\otimes I_{2}\otimes A_{2^{m-2}}=\left[{\begin{array}{cccc}A&0&0&0\\0&A&0&0\\0&0&A&0\\0&0&0&A\end{array}}\right].$

Теперь из определений A , A *, A ** Ui _имеем и Fj _мы ,

$A^{*}=F_{3}\cdots F_{m+1},A^{**}=F_{4}\cdots F_{m+1}$

$\Rightarrow A=F_{2}A^{*},A^{*}=F_{3}A^{**}$

$\Rightarrow A=A^{*}\left(A^{**}\right)^{-1}U_{2}A^{*},$

что дает рекуррентное соотношение для A _{2 ^м} в плане А _{2 ^{м -1}} и А _{2 ^{м -2}} .

Диагональная форма

При использовании угловых матриц переноса для выполнения расчетов как аналитически, так и численно удобно работать с их диагональными формами. Чтобы облегчить это, отношение рекурсии можно переписать непосредственно в терминах диагональных форм и матриц собственных векторов A , A * и A **.

Вспоминая, что решетка в нашем примере инвариантна к отражению в том смысле, что

$w\left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right)=w\left(\sigma _{k},\sigma _{j},\sigma _{i},\sigma _{l}\right)=w\left(\sigma _{i},\sigma _{l},\sigma _{k},\sigma _{j}\right),$

мы видим, что A — симметричная матрица (т. е. она диагонализируема ортогональной матрицей ). Итак, мы пишем

$A=\alpha _{m}PA_{d}P^{T},$

где A _d — диагональная матрица (нормализованная так, что ее наибольший численный элемент равен 1), α _m — наибольшее собственное значение A и P ^Т П = Я. ​Аналогично для A * и A ** имеем

$A^{*}=\alpha _{m-1}P^{*}A_{d}^{*}\left(P^{*}\right)^{T},$

$A^{**}=\alpha _{m-2}P^{**}A_{d}^{**}\left(P^{**}\right)^{T},$

где A _d *, A _d **, P * и P ** определяются аналогично A * и A **, т.е. в терминах меньших (нормализованных) диагональных форм и (ортогональных) матриц собственных векторов A _{2 ^{м -1}} и А _{2 ^{м -2}} .

Подставляя эти диагонализации в рекурсивное соотношение, получаем

$A_{t}=\kappa RA_{d}R^{T},$

где

$\kappa ={\frac {\alpha _{m}\alpha _{m-2}}{\alpha _{m-1}^{2}}},$

$R=\left(P^{*}\right)^{T}P,$

$A_{t}=A_{d}^{*}\left(R^{*}\right)^{T}\left(A_{d}^{**}\right)^{-1}U_{2}R^{*}A_{d}^{*}.$

Теперь A _t также симметричен и может быть вычислен, если , _{известны Ad} Ad ** _* и R * ; Диагонализация A _t затем дает его нормализованную диагональную форму A _d , его наибольшее собственное значение κ и его ортогональную матрицу собственных векторов R .

Приложения

Ожидаемое значение вращения

Матрицы углового переноса (или их диагональные формы) могут использоваться для расчета таких величин, как среднее значение вращения в определенном месте глубоко внутри решетки. Для полной решетки, приведенной ранее, среднее значение спина в центральном узле определяется выражением

$\left\langle \sigma _{1}\right\rangle ={\frac {1}{Z_{N}}}\sum _{all \atop spins}\sigma _{1}\prod _{all \atop faces}w\left(\sigma _{i},\sigma _{j},\sigma _{k},\sigma _{l}\right).$

Имея конфигурации, упорядоченные так, что A , как и раньше, является диагональю блока, мы можем определить 2 ^м ×2 ^м диагональная матрица

$S=\left[{\begin{array}{cc}I&0\\0&-I\end{array}}\right],$

такой, что

$\left\langle \sigma _{1}\right\rangle ={\frac {{\textrm {tr}}SA^{4}}{{\textrm {tr}}A^{4}}}={\frac {{\textrm {tr}}\alpha _{m}^{4}PSA^{4}P^{T}}{{\textrm {tr}}\alpha _{m}^{4}PA^{4}P^{T}}}={\frac {{\textrm {tr}}SA_{d}^{4}}{{\textrm {tr}}A_{d}^{4}}}.$

Функция разделения для каждого сайта

Другой важной величиной для моделей решетки является статистическая сумма на узел, вычисляемая в термодинамическом пределе и записываемая как

$\kappa =\lim _{N\rightarrow \infty }\left(Z_{N}\right)^{1/N}.$

В нашем примере это сводится к

$\kappa =\lim _{N\rightarrow \infty }\left(\alpha _{m}^{4}{\textrm {tr}}A_{d}^{4}\right)^{1/N}\sim \alpha _{m}^{4/N},$

поскольку tr A _d ⁴ является сходящейся суммой при m и Ad _{→ ∞} становится бесконечномерным. Кроме того, число граней 2 m ( m +1) приближается к числу узлов N в термодинамическом пределе, поэтому мы имеем

$\alpha _{m}\sim \kappa ^{m\left(m+1\right)/2},$

что согласуется с предыдущим уравнением, в котором является наибольшим собственным значением для At _κ . Другими словами, статистическая сумма на узел определяется в точности соотношением диагонализированной рекурсии для угловых матриц переноса в термодинамическом пределе; это позволяет κ аппроксимировать Ad _{с помощью итерационного процесса вычисления} для большой решетки.

Однако размеры задействованных матриц растут экспоненциально, и в реальных численных расчетах их необходимо усекать на каждом шаге. Один из способов сделать это — сохранить n наибольших собственных значений на каждом шаге для некоторого фиксированного n . В большинстве случаев последовательность аппроксимаций, полученная при n = 1,2,3,..., быстро сходится к точному значению (для точно решаемой модели).

См. также

• Трансфер-матричный метод

Ссылки

• Бакстер, Р.Дж. (1981), «Угловые трансфер-матрицы», Physica A , 106 (1–2): 18–27, Bibcode : 1981PhyA..106...18B , doi : 10.1016/0378-4371(81)90203- Х
• Бакстер, Р.Дж. (1982), Точно решенные модели в статистической механике , Лондон, Великобритания: Academic Press, ISBN  0-12-083180-5 , заархивировано из оригинала 20 марта 2012 г. , получено 7 ноября 2008 г.