Раскраска заболеваемости

В теории графов раскраска обычно подразумевает присвоение вершинам , ребрам или граням графа . меток — Раскраска инцидентности это специальная разметка графа , при которой каждому инцидентности ребра с вершиной присваивается цвет при определенных ограничениях.

Определения

Ниже G обозначает простой граф с непустым множеством вершин (непустым) V ( G ), множеством ребер E ( G ) и максимальной степенью Δ( G ).

Определение. Инциденция где определяется как пара ( v , e ), $v\in V(G)$ является конечной точкой $e\in E(G).$ Проще говоря, говорят, что вершина v инцидентна ребру e . Два инцидентности ( v , e ) и ( u , f ) называются смежными или соседними , если выполняется одно из следующих условий:

v знак равно ты , е ≠ ж
знак е равно ж , v ≠ ты
е знак равно { v , ты }, ж знак равно { ты , ш } и v ≠ ш .

Определение. Пусть I ( G множество всех инцидентностей G. ) — Раскраска инцидентности G — это функция $c:I(G)\to \mathbb {N}$ который принимает разные значения в соседних инцидентностях (мы используем упрощенное обозначение c ( v , u ) используется вместо c (( v , e )).) Минимальное количество цветов, необходимое для раскраски инцидентности графа G, известно как хроматическое число падения или число окраски падения G , представленное как $\chi _{i}(G).$ Это обозначение было введено Дженнифер Дж. Куинн Мэсси и Ричардом А. Бруальди в 1993 году.

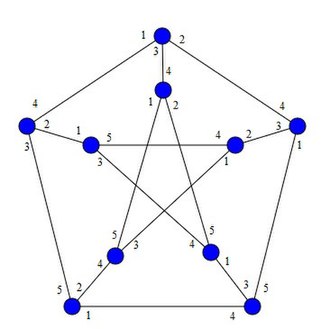
История

Концепция раскраски инцидентности была введена Бруальди и Мэсси в 1993 году, которые ограничили ее с помощью Δ( G ). Первоначально было выяснено хроматическое число инцидентности деревьев, полных двудольных графов и полных графов. Они также предположили, что все графы могут иметь раскраску инцидентности с использованием Δ( G ) + 2 цветов (гипотеза раскраски инцидентности — ICC). Эта гипотеза была опровергнута Гуйдули, который показал, что концепция раскраски падения представляет собой случай направленной звездной древесности, ^[1] представлены Алоном и Алгором. Его встречный пример показал, что хроматическое число падения не превышает Δ( G ) + O(log Δ( G )). ^[2]

Чен и др. нашел хроматическое число инцидентностей путей , вееров, циклов , колес, полного трехдольного графа и добавления реберных колес. Несколько лет спустя Шиу и др. показал, что эта гипотеза верна для некоторых кубических графов, таких как кубические гамильтоновы графы. Он показал, что в случае внешнепланарного графа максимальной степени 4 хроматическое число инцидентности не равно 5. В настоящее время установлены границы хроматического числа инцидентности различных классов графов.

Основные результаты

Предложение.

\chi _{i}(G)\geq \Delta (G)+1.

Доказательство. Пусть v — вершина максимальной степени Δ в G . Позволять $e_{1},e_{2},\ldots ,e_{\Delta }$ — ребра, инцидентные вершине v . Учитывать $e_{1}=\{v,w\}.$ Мы видим, что каждая пара инцидентов ∆ + 1, т. е. $(v,e_{1}),(v,e_{2}),\ldots ,(v,e_{\Delta }),(w,e_{1})$ является добрососедским. Поэтому эти случаи необходимо раскрасить разными цветами.

Оценка достигается деревьями и полными графами:

Если G — полный граф хотя бы с двумя вершинами, то $\chi _{i}(G)=\Delta (G)+1.$
Если G — дерево хотя бы с двумя вершинами, то $\chi _{i}(G)=\Delta (G)+1.$

Основные результаты были доказаны Бруальди и Мэсси (1993). Шиу, Сунь и Ву предложили некоторые необходимые условия для графа, удовлетворяющего $\chi _{i}(G)=\Delta (G)+1.$

$\chi _{i}(G)\leq 2\Delta (G).$
Хроматическое число инцидентности полного двудольного графа $K_{m,n}$ при m ≥ n ≥ 2 равно m + 2.
$\chi _{i}(C_{n})\leq 4$ и $\chi _{i}(C_{3n})=3.$

Раскраска инцидентности некоторых классов графов

Сетки

Введено несколько алгоритмов для обеспечения раскраски сеток. ^[3] такие как квадратные сетки , сотовые сетки и шестиугольные сетки. Эти алгоритмы являются оптимальными. Для каждой сетки цвета падения могут быть созданы за линейное время с наименьшим количеством цветов. Установлено, что ∆( G для раскраски падений квадратных, сотовых и шестиугольных сеток требуется ) + 1 цветов.

Хроматическое число падения квадратной сетки равно 5.
Хроматическое число падения шестиугольной сетки равно 7.
Хроматическое число падения сотовой сетки равно 4.

Графики Халина

Чен, Ван и Панг доказали, что если G — граф Халина с ∆( G ) > 4, то $\chi _{i}(G)=\Delta (G)+1.$ Для графов Халина с ∆( G ) = 3 или 4 Цзин-Чжэ Цюй показал $\chi _{i}(G)$ будет 5 или 6 соответственно. Является ли число раскраски инцидентности графов Халина низкой степени Δ( G ) + 1, до сих пор остается нерешенной проблемой.

Шиу и Сунь доказали каждый кубический граф Халина, кроме $K_{4}$ имеет раскраску инцидентности с Δ( G ) + 2 цвета. Су, Мэн и Го распространили этот результат на все псевдо-халинские графы.

Если граф Халина G содержит дерево T , то $\chi _{i}(G^{2})\leq \Delta (T^{2})+\Delta (T)+8.$ ^[4]

k-вырожденные графы

Д. Л. Чен, PCB Лам и В. К. Шиу выдвинули гипотезу, что хроматическое число инцидентности кубического графа G не превосходит ∆( G ) + 2. Они доказали это для некоторых кубических графов, таких как гамильтоновы кубические графы. На основе этих результатов М. Х. Долама, Э. Сопена и X. Чжу (2004) изучили классы графов, для которых $\chi _{i}(G)$ ограничен ∆( G ) + c , где c — некоторая фиксированная константа. ^[5] Граф называется k -порожденным, если для каждого подграфа H группы G минимальная степень H не превосходит k .

Хроматическое число инцидентности k -вырожденных графов G не превосходит ∆( G ) + 2 k − 1.
Хроматическое число инцидентности K ₄ минорных свободных графов G не превосходит ∆( G ) + 2 и образует жесткую границу.
Хроматическое число инцидентности планарного графа G не превосходит ∆( G ) + 7.

Внепланарные графы

Рассмотрим внешнепланарный граф G с разрезанной вершиной v такой, G – v является объединением что $H_{1}$ и $H_{2}$ . Позволять $G_{1}$ (соответственно $G_{2}$ ) — индуцированный подграф вершины v и вершин $H_{1}$ (соответственно $H_{2}$ ). Затем $\chi _{i}(G)$ это максимум из $\chi _{i}(G_{1}),\chi _{i}(G_{2})$ и $1+d_{G}(v)$ где $d_{G}(v)$ степень вершины v в G. —

Хроматическое число инцидентности внешнепланарного графа G не превышает ∆( G ) + 2. В случае внешнепланарных графов с ∆( G ) > 3 хроматическое число инцидентности равно ∆( G ) + 1.

Поскольку внешнепланарные графы являются K ₄ -минорными графами, они допускают (Δ + 2, 2)-раскраску инцидентности. ^[5]^[6] Решение для хроматического числа инцидентности внешнепланарного графа G, имеющего Δ( G ) = 3 и 2-связного внешнепланарного графа, остается открытым вопросом.

Хордальные кольца

Хордальные кольца представляют собой разновидности кольцевых сетей. Использование хордальных колец в коммуникации очень широко распространено из-за их преимуществ перед сетями взаимосвязей с кольцевой топологией и другими анализируемыми структурами, такими как сетки, гиперкубы, графы Кэли и т. д. Арден и Ли. ^[7] первым предложил хордальное кольцо степени 3, то есть сеть с кольцевой структурой, в которой каждый узел имеет дополнительную связь, известную как хорда, с каким-либо другим узлом в сети. Распределенные петлевые сети представляют собой хордальные кольца степени 4, которые строятся путем добавления двух дополнительных хорд в каждую вершину кольцевой сети.

Хордальное кольцо на N узлах и длине хорды d , обозначаемое CR ( N , d ), представляет собой граф, определяемый как:

{\begin{aligned}V(G)&=\{v_{0},v_{1},\ldots ,v_{N-1}\}\\E(G)&=\{v_{i}v_{j}:i-j\equiv 1,d{\bmod {N}}\}\end{aligned}}

Эти графы изучаются в связи с их применением в общении. Кунг-Фу Дин, Кунг-Джуй Пай и Ро-Ю Ву изучали раскраску хордальных колец. ^[8] Сформулировано несколько алгоритмов для определения хроматического числа инцидентности хордальных колец. Основные выводы:

{\begin{aligned}\chi _{i}(CR(N,2))&={\begin{cases}5&5|N\\6&{\text{otherwise}}\end{cases}}\\\chi _{i}(CR(N,3))&={\begin{cases}5&5|N\\6&N\equiv 2{\bmod {5}}\end{cases}}\end{aligned}}

Силы циклов

Кеайтсуда Накпрасит и Киттикорн Накпрасит изучали раскраску падения степеней циклов. $C_{n}^{k}.$ Если 2 k + 1 ≥ n, то $C_{n}^{k}=K_{n}$ поэтому предположим, что n > 2 k + 1, и напишем:

n=(2k+1)t+r,\quad 1\leq t,\quad 0\leq r\leq 2k.

Их результаты можно резюмировать следующим образом: ^[9]

{\begin{aligned}\chi _{i}(C_{n}^{k})&={\begin{cases}2k+1&r=0\\2k+2&1\leq r\leq t{\text{ or }}r=2k\end{cases}}&&k\geq 3\\\chi _{i}(C_{n}^{2})&={\begin{cases}5&5|n\\6&{\text{otherwise}}\end{cases}}\end{aligned}}

Связь с гипотезой о раскраске инцидентности определяется наблюдением, что $\Delta (C_{n}^{k})=2k.$

Связь между хроматическим числом инцидентности и числом доминирования графа

Предложение. ^[10] Пусть G — простой связный граф порядка n , размера m и числа доминирования.

\gamma .

Затем

\chi _{i}(G)\geq {\tfrac {2m}{n-\gamma }}.

Доказательство. Сформируйте орграф D ( G ) из графа G , разделив каждое ребро G на 2 дуги в противоположных направлениях. Мы видим, что общее количество дуг в D ( G ) равно 2 м . По словам Гуйдули, ^[2] раскраска инцидентности G эквивалентна правильной раскраске орграфа D ( G ), где 2 различные дуги ${\overrightarrow {uv}}$ и ${\overrightarrow {xy}}$ смежны, если выполнено одно из следующих условий: (i) u = x ; (ii) v = x или y = u . По определению смежности дуг независимый набор дуг в D ( G ) представляет собой звездный лес. Следовательно, максимальный независимый набор дуг представляет собой максимальный звездный лес . Это означает, что по крайней мере ${\tfrac {2m}{n-\gamma }}$ необходимы классы цвета. ^[10]

Это соотношение широко использовалось при описании -регулярных графов ( r + 1)-инцидентности раскрашиваемых r . Основной результат по раскраске инцидентности r -регулярных графов таков: если граф G является r-регулярным графом , то $\chi _{i}(G)=\chi _{i}(G^{2})=r+1$ тогда и только тогда, когда V ( G ) — дизъюнктное объединение r +1 доминирующих множеств . ^[10]

Раскраска интервальной заболеваемости

Определение. Конечное подмножество $A\subset \mathbb {N}$ является интервалом тогда и только тогда, когда он содержит все числа между минимумом и максимумом.

Определение. Пусть c — раскраска инцидентности G и определим

A_{c}(v)=\{c(v,e):(v,e)\in I(G)\}.

Интервальная раскраска инцидентности графа G — это раскраска инцидентности c такая, что для каждой вершины v графа G множество $A_{c}(v)$ является интервалом. ^[11]^[12] Число окраски интервальной инцидентности G инцидентности — это минимальное количество цветов, используемых для окраски интервальной G . Это обозначается $\chi _{ii}.$ Ясно, что $\chi _{i}(G)\leq \chi _{ii}(G).$ Если бы только $\chi _{ii}$ цвета используются для раскраски интервала падения, тогда он называется минимальным.

Понятие интервальной окраски инцидентности было введено А. Малафиейской, Р. Янчевским и М. Малафейским. Они доказали $\chi _{ii}(G)\leq \Delta (G)$ для двудольных графов. ^[13] В случае регулярных двудольных графов равенство имеет место. Субкубические двудольные графы допускают интервальную раскраску с использованием четырех, пяти или шести цветов. Они также доказали, что 5-раскраска инцидентности может быть решена за линейное время для двудольных графов с ∆( G ) = 4.

Раскраска дробного падения

Дробная версия инцидентной раскраски была впервые представлена Янгом в 2007 году. r -кортежная k -раскраска инцидентности графа G — это присвоение r цветов каждой инцидентности графа G из набора k цветов, так что соседние инцидентности даны непересекающиеся множества цветов. ^[14] По определению очевидно, что 1-кратная инцидентность k -раскраски также является инцидентностью k -раскраски.

Хроматическое число дробного падения графа G — это нижняя грань дробей. ${\tfrac {k}{r}}$ таким образом, что G допускает r -кратную инцидентность k -раскраски. Раскраска дробного падения имеет большое применение в нескольких областях информатики. На основе результатов окраски падения по Гуйдули, ^[2] Ян доказал, что дробное хроматическое число инцидентности любого графа не превышает Δ( G ) + 20 log Δ( G ) + 84. Он также доказал существование графов с дробным хроматическим числом инцидентности не менее Δ( G ) + Ω. (логарифм Δ( G )).

Неравенство Нордхауса – Гаддума.

Пусть G — граф с n вершинами такой, что $G\neq K_{n},{\overline {K_{n}}}$ где ${\overline {G}}$ обозначает дополнение G . Затем $n+2\leq \chi _{i}(G)+\chi _{i}({\overline {G}})\leq 2n-1.$ ^[10] Эти границы точны для всех значений n .

Игра-раскраска заболеваемости

Игра-раскраска инцидентов была впервые представлена SD Andres. ^[15] Это инцидентная версия игры с раскраской вершин, в которой вместо вершин раскрашиваются инцидентности графа. Хроматическое число игры инцидентности — это новый параметр, определяемый как теоретико-игровой аналог хроматического числа инцидентности.

Игра заключается в том, что два игрока, Алиса и Боб, создают правильную раскраску инцидентности. Правила изложены ниже:

Алиса и Боб раскрашивают инцидентности графа G набором k цветов.
Они по очереди придают правильную окраску неокрашенному падению. В общем, начинается Алиса.
В случае инцидента, который невозможно правильно раскрасить, побеждает Боб.
Если все вхождения графа раскрашены правильно, Алиса выигрывает.

Хроматическое число игры инцидентности графа G , обозначаемое $i_{g}(G)$ , — это наименьшее количество цветов, необходимое Алисе для победы в игре-раскраске по падению. Он объединяет идеи хроматического числа инцидентности графа и игрового хроматического числа в случае неориентированного графа. Андрес обнаружил, что верхняя граница для $i_{g}(G)$ в случае k -вырожденных графов равно 2Δ + 4 k − 2. Эта оценка была улучшена до 2Δ + 3 k − 1 в случае графов, в которых Δ не менее 5 k . Также определяется падение игрового хроматического числа звезд, циклов и достаточно больших колес. ^[15] Джон Ю. Ким (2011) нашел точное хроматическое число больших путей в игре инцидентности и дал правильное доказательство результата, заявленного Андресом, относительно точного хроматического числа больших колес в игре инцидентности. ^[16]

Ссылки

^ Алгор И., Алон Н. (1989); « Звездная древовидность графов », Дискретная математика 75, стр. 11-22.
^ Jump up to: ^а ^б ^с Гуйдули Б. (1997); « О раскраске инцидентности и звездной древовидности графов », Дискретная математика 163, стр. 275-278.
^ Хуанг, CI; Ван, ЮЛ; Чунг, С.С. (2004), « Числа раскраски сеток », Компьютеры и математика с приложениями 48, стр. 1643–1649.
^ Ван, С.Д.; Ченг, Д.Л.; Панг, SC (2002), « Число раскраски инцидентности графов Халина и внешнепланарных графов », Discrete Mathematics 256, стр. 397–405.
^ Jump up to: ^а ^б Хоссейни Долама, М.; Сопена, Э.; Чжу, X. (2004), « Раскраска инцидентности k-сгенерированных графов », Discrete Mathematics 283, стр. 121–128.
^ Ван, С.; Сюй, Дж.; Ма, Ф.; Сюй, К. (2008), « Раскраска (Δ + 2, 2)-инцидентности внешнепланарных графов », Progress in Natural Science 18, стр. 575–578.
^ Арден Б.В., Ли Х. (1981); « Анализ хордальной кольцевой сети », Транзакции IEEE на компьютерах 30, стр. 291–295.
^ Дин К.Ф., Пай К.Дж., Ю Р. (1981); « Некоторые результаты по числу раскрасок инцидентности хордальных колец * », 32-й семинар по комбинаторной математике и теории вычислений, стр. 89-93.
^ Накпрасит, Кейтсуда и Накпрасит, Киттикорн (2012), « Раскраски инцидентности степеней циклов », Международный журнал чистой и прикладной математики 76 (1), стр. 143–148
^ Jump up to: ^а ^б ^с ^д Сан, ПК (2012), « Раскраска инцидентности регулярных графов и дополнительных графов », Тайваньский математический журнал 16, № 6, стр. 2289–2295.
^ Янчевский, Р.; Малафейская, А.; Малафейский, М., «Назначение интервальных длин волн в полностью оптических звездных сетях», Параллельная обработка и прикладная математика, 8-я Международная конференция, PPAM 2009, Втроцлав, Польша, 13–16 сентября 2009 г. Пересмотренные избранные статьи, часть I (Springer), стр. 11–20, doi:10.1007/978-3-642-14390-8_2, ISBN 978-3-642-14389-2
^ Янчевский, Р.; Малафейская, А.; Малафейский, М. (2015), « Раскраска интервального графа инцидентности », Дискретная прикладная математика 182, стр. 73–83.
^ Янчевский, Р.; Малафейская, А.; Малафиейский, М. (2014), « Интервальная раскраска двудольных графов », Дискретная прикладная математика 166, стр. 131–145.
^ Ян, Д. (2012), « Дробная раскраска инцидентности и звездная древовидность графов », Ars Combinatoria - Ватерлоо, затем Виннипег 105, стр. 213–224
^ Jump up to: ^а ^б Андрес, С.Д. (2009), « Хроматическое число игры инцидентности », Discrete Applied Mathematics 157, стр. 1980–1987.
^ Ким, JY (2011), « Хроматическое число путей и подграфов колес в игре инцидентности », Discrete Applied Mathematics 159, стр. 683–694

Дополнительные ссылки

Майданский, М. (2005), "Гипотеза о раскраске инцидентности для графов максимальной степени 3" , Дискретная математика , т. 1, с. 292, стр. 131–141 .
Хартке, С.Г.; Helleloid, GT (2012), «Реконструкция графа по графу инцидентности дуг», Graphs and Combinatorics , vol. 28, стр. 637–652, номер документа : 10.1007/s00373-011-1073-7 , S2CID 14656326 .
Солнце, ПК; Шиу, WC (2012), «Неверные доказательства раскраски инцидентности» (PDF) , Discrete Mathematics , vol. 54, стр. 107–114 .
Ли, Д; Лю, М. (2008), «Раскраска инцидентности квадратов некоторых графов» , Дискретная математика , том. 308, стр. 6575–6580 .
Бонами, М.; Хоккард, Х.; Керджудж, С.; Распауд, А. (2015), Раскраска заболеваемости графиков с высокой максимальной средней степенью , arXiv : 1412.6803 , Bibcode : 2014arXiv1412.6803B .
Хоссейни Долама, М.; Сопена, Э. (2005), «О максимальной средней степени и частоте хроматического числа графа» (PDF) , Discrete Mathematics and Theoretical Computer Science , vol. 7, стр. 203–216 .
Шиу, туалет; Лам, PCP; Чен, Д.Л. (2002), «О раскраске инцидентности некоторых кубических графов» , Discrete Mathematics , vol. 252, стр. 259–266, doi : 10.1016/S0012-365X(01)00457-5 .
Накпрасит, К. (2014), «Сильный хроматический индекс графов и подразделений» , Дискретная математика , том. 317, стр. 75–78 .
Дин, К.Ф.; Пай, К.Дж.; Чанг, Дж. М.; Цаур, Р. (2015), «Некоторые результаты раскраски инцидентности обобщенных графов Петерсена», Интеллектуальные системы и приложения: материалы Международного компьютерного симпозиума (ICS), состоявшегося в Тайчжуне, Тайвань, 12–14 декабря 2014 г. , том. 274, IOS Press, стр. 85–91, doi : 10.3233/978-1-61499-484-8-85 .
Лян, Л.; Гао, В. (2010), «О хроматическом числе дробного падения обобщенного тета-графа» , Журнал Чунцинского педагогического университета , том. 27, стр. 36–39 .
Шиу, туалет; Лам, печатная плата; Чен, Д.Л. (2002), «Примечание о раскраске инцидентности для некоторых кубических графов» , Discrete Mathematics , vol. 252, стр. 259–266 .
Солнце, ПК; Шиу, WC (2012), «Некоторые результаты по окраске падения, древесности звезд и числу доминирования» (PDF) , Австралазийский журнал комбиниторики , том. 54, стр. 107–114 .
Ву, Дж. (2009), «Некоторые результаты о числе раскраски графа» , Discrete Mathematics , vol. 309, стр. 3866–3870 .
Ли, Х.; Ту, Дж. (2008), «NP-полнота раскрашиваемости полукубических графов с 4 инцидентностями» , Discrete Mathematics , vol. 308, стр. 1334–1340 .
Пай, К.Дж.; Чанг, Дж. М.; Ву, Р.Ю. (2014), «Раскраска инцидентности гиперкубов» , Theoretical Computer Science , vol. 557, стр. 59–65 .
Пай, К.Дж.; Чанг, Дж. М.; Ву, Р.Ю. (2014), «О числе раскраски свернутых гиперкубов» , Материалы 18-й Международной конференции по компьютерным наукам и инженерии (ICSEC 2014), 30 июля — 1 августа, Кхон Каен, Таиланд , стр. 7–11 .
Сопена, Э.; Ву, Дж (2013), «Хроматическое число инцидентности тороидальных сеток», Дискуссии Mathematicae Graph Theory , 33 (2): 315–327, arXiv : 0907.3801 , doi : 10.7151/dmgt.1663 , S2CID 1313615 .
Андрес, С.Д. (2009). «Ошибка: Хроматическое число игры с инцидентностью» . Дискретная прикладная математика . 158 (6): 728. doi : 10.1016/j.dam.2009.11.017 .
Шарпантье, К.; Сопена, Э. (2015), «Хроматическое число игры инцидентности (a,d)-разложимых графов» , Journal of Discrete Algorithms , vol. 31, стр. 14–25 .
Ву, Дж.; Чжу, X. (2008), «6-расслабленное игровое хроматическое число внешнепланарных графов», Discrete Mathematics , 308 (24): 5974–5980, doi : 10.1016/j.disc.2007.11.015 .
Мэн, X.; Го, Дж.; Су, Б. (2012), «Раскраска инцидентности псевдографов Халина» , Discrete Mathematics , 312 (22): 3276–3282, doi : 10.1016/j.disc.2012.07.024 .
Андрес, С.Д. (2009), «Легкость орграфов на поверхностях и хроматическое число направленной игры» , Дискретная математика , том. 309, стр. 3564–3579 .
Ли, Х.; Ту, Дж. (2008), «NP-полнота раскрашиваемости полукубических графов с 4 инцидентностями» , Discrete Mathematics , 308 (7): 1334–1340, arXiv : math/0607071 , doi : 10.1016/j.disc. 2007.03.076 , S2CID 59464 .
Чжу, X. (1999), «Количество раскраски плоских графов в игре», Журнал комбинаторной теории, серия B , 75 (2): 245–258, doi : 10.1006/jctb.1998.1878 .
Лю, X.; Ли, Ю. (2005), «Хроматическое число инцидентности некоторого графа», Международный журнал математики и математических наук , 1 (5): 803–813, doi : 10.1155/IJMMS.2005.803 .
Донг, GX; Лю, XF (2014), «Количество раскраски инцидентности некоторых графов соединений» , Applied Mechanics and Materials , 602–605: 3185–3188, doi : 10.4028/www.scientific.net/AMM.602-605.3185 , S2CID 122567953 .

См. также

[1] Алгор И., Алон Н. (1989); « Звездная древовидность графов », Дискретная математика 75, стр. 11-22.

[gb-2] Jump up to: ^а ^б ^с Гуйдули Б. (1997); « О раскраске инцидентности и звездной древовидности графов », Дискретная математика 163, стр. 275-278.

[3] Хуанг, CI; Ван, ЮЛ; Чунг, С.С. (2004), « Числа раскраски сеток », Компьютеры и математика с приложениями 48, стр. 1643–1649.

[4] Ван, С.Д.; Ченг, Д.Л.; Панг, SC (2002), « Число раскраски инцидентности графов Халина и внешнепланарных графов », Discrete Mathematics 256, стр. 397–405.

[dsz-5] Jump up to: ^а ^б Хоссейни Долама, М.; Сопена, Э.; Чжу, X. (2004), « Раскраска инцидентности k-сгенерированных графов », Discrete Mathematics 283, стр. 121–128.

[6] Ван, С.; Сюй, Дж.; Ма, Ф.; Сюй, К. (2008), « Раскраска (Δ + 2, 2)-инцидентности внешнепланарных графов », Progress in Natural Science 18, стр. 575–578.

[7] Арден Б.В., Ли Х. (1981); « Анализ хордальной кольцевой сети », Транзакции IEEE на компьютерах 30, стр. 291–295.

[8] Дин К.Ф., Пай К.Дж., Ю Р. (1981); « Некоторые результаты по числу раскрасок инцидентности хордальных колец * », 32-й семинар по комбинаторной математике и теории вычислений, стр. 89-93.

[nk-9] Накпрасит, Кейтсуда и Накпрасит, Киттикорн (2012), « Раскраски инцидентности степеней циклов », Международный журнал чистой и прикладной математики 76 (1), стр. 143–148

[sk-10] Jump up to: ^а ^б ^с ^д Сан, ПК (2012), « Раскраска инцидентности регулярных графов и дополнительных графов », Тайваньский математический журнал 16, № 6, стр. 2289–2295.

[11] Янчевский, Р.; Малафейская, А.; Малафейский, М., «Назначение интервальных длин волн в полностью оптических звездных сетях», Параллельная обработка и прикладная математика, 8-я Международная конференция, PPAM 2009, Втроцлав, Польша, 13–16 сентября 2009 г. Пересмотренные избранные статьи, часть I (Springer), стр. 11–20, doi:10.1007/978-3-642-14390-8_2, ISBN 978-3-642-14389-2

[12] Янчевский, Р.; Малафейская, А.; Малафейский, М. (2015), « Раскраска интервального графа инцидентности », Дискретная прикладная математика 182, стр. 73–83.

[13] Янчевский, Р.; Малафейская, А.; Малафиейский, М. (2014), « Интервальная раскраска двудольных графов », Дискретная прикладная математика 166, стр. 131–145.

[14] Ян, Д. (2012), « Дробная раскраска инцидентности и звездная древовидность графов », Ars Combinatoria - Ватерлоо, затем Виннипег 105, стр. 213–224

[an-15] Jump up to: ^а ^б Андрес, С.Д. (2009), « Хроматическое число игры инцидентности », Discrete Applied Mathematics 157, стр. 1980–1987.

[16] Ким, JY (2011), « Хроматическое число путей и подграфов колес в игре инцидентности », Discrete Applied Mathematics 159, стр. 683–694

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]