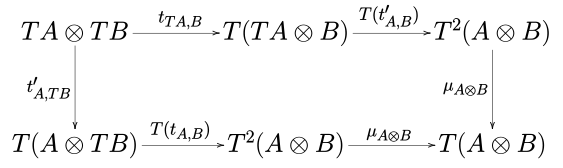Сильная монада

Сильная монада — это математический объект, определенный с помощью теории категорий , которая используется в теоретической информатике . Говоря техническим языком, сильная монада над моноидальной категорией ( C , ⊗, I) — это монада ( T , η, µ) вместе с естественным преобразованием t _A,B : A ⊗ TB → T ( A ⊗ B ), называемым ( тензорная ) сила , такая, что диаграммы

, ,

, и

коммутируют для каждого объекта A , B и C (см. определение 3.2 в ).

Если моноидальная категория ( C , ⊗, I) замкнута , то сильная монада — это то же самое, что C -обогащенная монада.

Коммутативные сильные монады

Для каждой сильной монады T в симметричной моноидальной категории естественное преобразование стоимости может быть определено формулой

$$t'_{A,B}=T(\gamma _{B,A})\circ t_{B,A}\circ \gamma _{TA,B}:TA\otimes B\to T(A\otimes B).$$

Сильная монада T называется коммутативной, если диаграмма

ездит на все объекты $A$ и $B$.

Один интересный факт о коммутативных сильных монадах заключается в том, что они «такие же, как» симметричные моноидальные монады . Более явно,

• коммутативная сильная монада $(T,\eta ,\mu ,t)$ определяет симметричную моноидальную монаду $(T,\eta ,\mu ,m)$ к $$m_{A,B}=\mu _{A\otimes B}\circ Tt'_{A,B}\circ t_{TA,B}:TA\otimes TB\to T(A\otimes B)$$
• и наоборот симметричная моноидальная монада $(T,\eta ,\mu ,m)$ определяет коммутативную сильную монаду $(T,\eta ,\mu ,t)$ к $$t_{A,B}=m_{A,B}\circ (\eta _{A}\otimes 1_{TB}):A\otimes TB\to T(A\otimes B)$$

и преобразование между одним и другим представлением является биективным.

Ссылки

• Андерс Кок (1972). «Сильные функторы и моноидальные монады» (PDF) . Архив математики . 23 : 113–120. дои : 10.1007/BF01304852 . S2CID   13246783 .
• Жан Губо-Ларрек, Славомир Ласота и Дэвид Новак (2005). «Логические отношения для монадических типов». Математические структуры в информатике . 18 (6): 1169. arXiv : cs/0511006 . дои : 10.1017/S0960129508007172 . S2CID   741758 .

Внешние ссылки

• Сильная монада в nLab