Ядро более гладкое

Сглаживатель ядра - это статистический метод оценки действительной функции. $f:\mathbb {R} ^{p}\to \mathbb {R}$ как средневзвешенное значение соседних наблюдаемых данных. Вес определяется ядром , так что более близким точкам присваиваются более высокие веса. Оцениваемая функция является гладкой, а уровень гладкости задается одним параметром.Ядерное сглаживание — это разновидность взвешенной скользящей средней .

Определения

Позволять $K_{h_{\lambda }}(X_{0},X)$ быть ядром, определяемым

$K_{h_{\lambda }}(X_{0},X)=D\left({\frac {\left\|X-X_{0}\right\|}{h_{\lambda }(X_{0})}}\right)$

где:

• $X,X_{0}\in \mathbb {R} ^{p}$
• $\left\|\cdot \right\|$ это евклидова норма
• $h_{\lambda }(X_{0})$ это параметр (радиус ядра)
• D ( t ) обычно является положительной вещественной функцией, значение которой уменьшается (или не увеличивается) с увеличением расстояния X и X0 _между .

Популярные ядра, используемые для сглаживания, включают параболическое ядро ​​(Епанечникова), трехкубическое и гауссовское .

Позволять $Y(X):\mathbb {R} ^{p}\to \mathbb {R}$ быть непрерывной функцией X . Для каждого $X_{0}\in \mathbb {R} ^{p}$средневзвешенное по ядру Надарая-Ватсона (гладкая оценка Y ( X )) определяется выражением

${\hat {Y}}(X_{0})={\frac {\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})Y(X_{i})}}{\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})}}}$

где:

• N — количество наблюдаемых точек
• Y ( X _i ) — наблюдения в точках X _i .

В следующих разделах мы опишем некоторые частные случаи сглаживателей ядра.

Гауссово ядро ​​более гладкое

Ядро Гаусса является одним из наиболее широко используемых ядер и выражается уравнением, приведенным ниже.

$K(x^{*},x_{i})=\exp \left(-{\frac {(x^{*}-x_{i})^{2}}{2b^{2}}}\right)$

Здесь b — масштаб длины входного пространства.

Ближайший сосед более плавный

Идея сглаживания ближайшего соседа заключается в следующем. Для каждой точки X ₀ возьмите m ближайших соседей и оцените значение Y ( X ₀ ) путем усреднения значений этих соседей.

Формально, $h_{m}(X_{0})=\left\|X_{0}-X_{[m]}\right\|$, где $X_{[m]}$ является m- м ближайшим к X ₀ соседом, и

$D(t)={\begin{cases}1/m&{\text{if }}|t|\leq 1\\0&{\text{otherwise}}\end{cases}}$

Пример:

В этом примере X является одномерным. Для каждого ₀ X ${\hat {Y}}(X_{0})$ представляет собой среднее значение из 16 ближайших к X ₀ баллов (обозначено красным).

Ядро в среднем более плавное

Идея сглаживания среднего ядра заключается в следующем. Для каждой точки данных X ₀ выберите постоянный размер расстояния λ (радиус ядра или ширину окна для измерения p = 1) и вычислите средневзвешенное значение для всех точек данных, которые находятся ближе, чем $\lambda$ до X ₀ (точки, расположенные ближе к X _0, получают больший вес).

Формально, $h_{\lambda }(X_{0})=\lambda ={\text{constant}},$ и D ( t ) — одно из популярных ядер.

Пример:

Для каждого X ₀ ширина окна постоянна, а вес каждой точки окна схематически обозначен желтой цифрой на графике. Видно, что оценка гладкая, но граничные точки смещены. Причиной тому является неодинаковое количество точек (справа и слева от X ₀ ) в окне, когда X ₀ находится достаточно близко к границе.

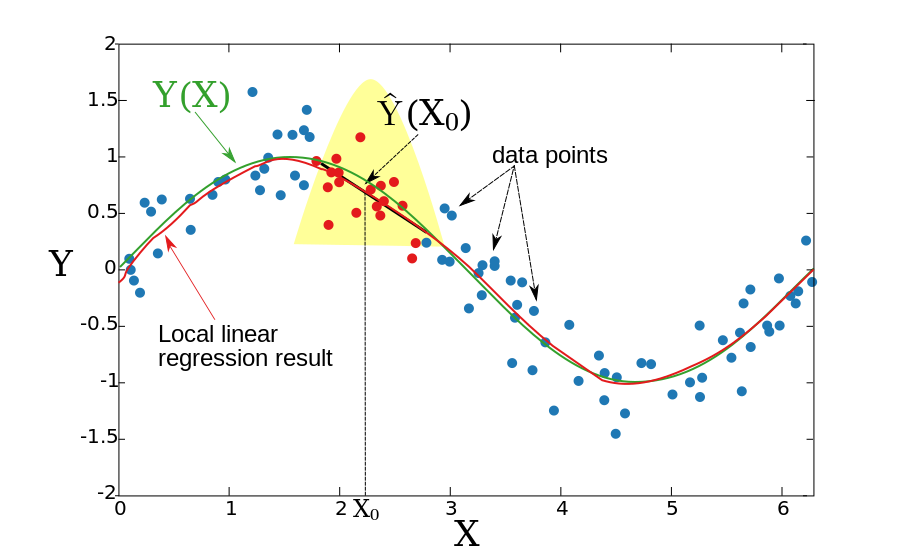
Локальная линейная регрессия

Основная статья: Локальная регрессия

В двух предыдущих разделах мы предполагали, что базовая функция Y(X) является локально постоянной, поэтому мы смогли использовать для оценки средневзвешенное значение. Идея локальной линейной регрессии состоит в том, чтобы локально соответствовать прямой линии (или гиперплоскости для более высоких измерений), а не константе (горизонтальной линии). После подгонки линии оценка ${\hat {Y}}(X_{0})$ обеспечивается значением этой линии в точке X ₀ . Повторяя эту процедуру для каждого X ₀ , можно получить оценочную функцию ${\hat {Y}}(X)$.Как и в предыдущем разделе, ширина окна постоянна. $h_{\lambda }(X_{0})=\lambda ={\text{constant}}.$Формально локальная линейная регрессия вычисляется путем решения взвешенной задачи наименьших квадратов.

Для одного измерения ( p = 1):

${\begin{aligned}&\min _{\alpha (X_{0}),\beta (X_{0})}\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-\alpha (X_{0})-\beta (X_{0})X_{i}\right)^{2}}\\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Downarrow \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\hat {Y}}(X_{0})=\alpha (X_{0})+\beta (X_{0})X_{0}\\\end{aligned}}$

Решение в закрытой форме определяется следующим образом:

${\hat {Y}}(X_{0})=\left(1,X_{0}\right)\left(B^{T}W(X_{0})B\right)^{-1}B^{T}W(X_{0})y$

где:

• $y=\left(Y(X_{1}),\dots ,Y(X_{N})\right)^{T}$
• $W(X_{0})=\operatorname {diag} \left(K_{h_{\lambda }}(X_{0},X_{i})\right)_{N\times N}$
• $B^{T}=\left({\begin{matrix}1&1&\dots &1\\X_{1}&X_{2}&\dots &X_{N}\\\end{matrix}}\right)$

Пример:

Полученная функция является гладкой, и проблема со смещенными граничными точками уменьшается.

Локальную линейную регрессию можно применять к любому размерному пространству, хотя вопрос о том, что такое локальная окрестность, становится более сложным. Обычно используется k ближайших точек обучения к контрольной точке, чтобы соответствовать локальной линейной регрессии. Это может привести к высокой дисперсии подобранной функции. Чтобы ограничить дисперсию, набор обучающих точек должен содержать тестовую точку в своей выпуклой оболочке (см. ссылку Гупта и др.).

Локальная полиномиальная регрессия

Вместо подгонки локально линейных функций можно подогнать полиномиальные функции.

При p=1 следует минимизировать:

${\underset {\alpha (X_{0}),\beta _{j}(X_{0}),j=1,...,d}{\mathop {\min } }}\,\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-\alpha (X_{0})-\sum \limits _{j=1}^{d}{\beta _{j}(X_{0})X_{i}^{j}}\right)^{2}}$

с ${\hat {Y}}(X_{0})=\alpha (X_{0})+\sum \limits _{j=1}^{d}{\beta _{j}(X_{0})X_{0}^{j}}$

В общем случае (p>1) следует минимизировать:

${\begin{aligned}&{\hat {\beta }}(X_{0})={\underset {\beta (X_{0})}{\mathop {\arg \min } }}\,\sum \limits _{i=1}^{N}{K_{h_{\lambda }}(X_{0},X_{i})\left(Y(X_{i})-b(X_{i})^{T}\beta (X_{0})\right)}^{2}\\&b(X)=\left({\begin{matrix}1,&X_{1},&X_{2},...&X_{1}^{2},&X_{2}^{2},...&X_{1}X_{2}\,\,\,...\\\end{matrix}}\right)\\&{\hat {Y}}(X_{0})=b(X_{0})^{T}{\hat {\beta }}(X_{0})\\\end{aligned}}$

См. также

• Фильтр Савицкого – Голея
• Методы ядра
• Оценка плотности ядра
• Локальная регрессия
• Регрессия ядра

Ссылки

• Ли, К. и Дж. С. Расин. Непараметрическая эконометрика: теория и практика . Издательство Принстонского университета, 2007 г., ISBN   0-691-12161-3 .
• Т. Хасти, Р. Тибширани и Дж. Фридман, Элементы статистического обучения , глава 6, Springer, 2001. ISBN   0-387-95284-5 ( сайт сопутствующей книги ).
• М. Гупта, Э. Гарсия и Э. Чин, «Адаптивная локальная линейная регрессия с применением к управлению цветом принтера», IEEE Trans. Обработка изображений 2008.