Регрессия ядра

Не путать с анализом главных компонентов ядра или регрессией гребня ядра .

В статистике — ядерная регрессия это непараметрический метод оценки условного ожидания случайной величины . чтобы найти нелинейную связь между парой случайных величин X и Y. Цель состоит в том ,

В любой непараметрической регрессии условное ожидание переменной $Y$ относительно переменной $X$ можно написать:

$\operatorname {E} (Y\mid X)=m(X)$

где $m$ это неизвестная функция.

-

Надарая и Уотсон в 1964 году предложили оценить $m$ как локально взвешенное среднее с использованием ядра в качестве весовой функции. Оценщик Надарая-Ватсона:

${\widehat {m}}_{h}(x)={\frac {\sum _{i=1}^{n}K_{h}(x-x_{i})y_{i}}{\sum _{i=1}^{n}K_{h}(x-x_{i})}}$

где $K_{h}(t)={\frac {1}{h}}K\left({\frac {t}{h}}\right)$ это ядро ​​с пропускной способностью $h$ такой, что $K(\cdot )$ имеет порядок не менее 1, то есть $\int _{-\infty }^{\infty }uK(u)\,du=0$.

Вывод

Начнем с определения условного ожидания .

$\operatorname {E} (Y\mid X=x)=\int yf(y\mid x)\,dy=\int y{\frac {f(x,y)}{f(x)}}\,dy$

мы оцениваем совместные распределения f ( x , y ) и f ( x ), используя оценку плотности ядра с ядром K :

${\hat {f}}(x,y)={\frac {1}{n}}\sum _{i=1}^{n}K_{h}(x-x_{i})K_{h}(y-y_{i}),$

${\hat {f}}(x)={\frac {1}{n}}\sum _{i=1}^{n}K_{h}(x-x_{i}),$

Мы получаем:

${\begin{aligned}\operatorname {\hat {E}} (Y\mid X=x)&=\int y{\frac {{\hat {f}}(x,y)}{{\hat {f}}(x)}}\,dy,\\[6pt]&=\int y{\frac {\sum _{i=1}^{n}K_{h}(x-x_{i})K_{h}(y-y_{i})}{\sum _{j=1}^{n}K_{h}(x-x_{j})}}\,dy,\\[6pt]&={\frac {\sum _{i=1}^{n}K_{h}(x-x_{i})\int y\,K_{h}(y-y_{i})\,dy}{\sum _{j=1}^{n}K_{h}(x-x_{j})}},\\[6pt]&={\frac {\sum _{i=1}^{n}K_{h}(x-x_{i})y_{i}}{\sum _{j=1}^{n}K_{h}(x-x_{j})}},\end{aligned}}$

что является оценщиком Надарайи – Ватсона.

Оценщик ядра Пристли – Чао

${\widehat {m}}_{PC}(x)=h^{-1}\sum _{i=2}^{n}(x_{i}-x_{i-1})K\left({\frac {x-x_{i}}{h}}\right)y_{i}$

где $h$ — это полоса пропускания (или параметр сглаживания).

Оценка ядра Гассера-Мюллера

${\widehat {m}}_{GM}(x)=h^{-1}\sum _{i=1}^{n}\left[\int _{s_{i-1}}^{s_{i}}K\left({\frac {x-u}{h}}\right)\,du\right]y_{i}$

где $s_{i}={\frac {x_{i-1}+x_{i}}{2}}.$

Пример

Предполагаемая функция регрессии.

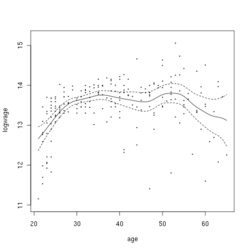
Этот пример основан на перекрестных данных о заработной плате в Канаде, состоящих из случайной выборки, взятой из записей публичного использования Канадской переписи населения 1971 года для лиц мужского пола, имеющих общее образование (13 класс). Всего 205 наблюдений.

На рисунке справа показана оцененная функция регрессии с использованием ядра Гаусса второго порядка вместе с асимптотическими границами изменчивости.

Пример сценария

Следующие команды языка программирования R используют npreg() функция для обеспечения оптимального сглаживания и создания фигуры, приведенной выше. Эти команды можно вводить в командной строке с помощью вырезания и вставки.

install.packages("np")
library(np) # non parametric library
data(cps71)
attach(cps71)

m <- npreg(logwage~age)

plot(m, plot.errors.method="asymptotic",
     plot.errors.style="band",
     ylim=c(11, 15.2))

points(age, logwage, cex=.25)
detach(cps71)

Похожие

По словам Дэвида Сальсбурга , алгоритмы, используемые в ядерной регрессии, были независимо разработаны и использовались в нечетких системах : «Поскольку придуманы почти одинаковые компьютерные алгоритмы, нечеткие системы и регрессии на основе плотности ядра, по-видимому, были разработаны совершенно независимо друг от друга. "

реализация

• GNU Octave Пакет математических программ
• Юлия : KernelEstimator.jl
• MATLAB доступен бесплатный набор инструментов MATLAB с реализацией регрессии ядра, оценкой плотности ядра, оценкой функции риска и многими другими : на этих страницах (этот набор инструментов является частью книги). ).
• Питон : KernelReg класс для смешанных типов данных в statsmodels.nonparametric подпакет (включает другие классы, связанные с плотностью ядра), пакет kernel_reгрессия как расширение scikit-learn (неэффективно с точки зрения памяти, полезно только для небольших наборов данных)
• Р : функция npreg пакета np может выполнять регрессию ядра.
• Стата : npregress , kernreg2.

См. также

• Ядро более гладкое
• Локальная регрессия

Дальнейшее чтение

• Хендерсон, Дэниел Дж.; Парметр, Кристофер Ф. (2015). Прикладная непараметрическая эконометрика . Издательство Кембриджского университета. ISBN  978-1-107-01025-3 .
• Ли, Ци; Расин, Джеффри С. (2007). Непараметрическая эконометрика: теория и практика . Издательство Принстонского университета. ISBN  978-0-691-12161-1 .
• Пэган, А.; Улла, А. (1999). Непараметрическая эконометрика . Издательство Кембриджского университета. ISBN  0-521-35564-8 .
• Расин, Джеффри С. (2019). Введение в продвинутую теорию и практику непараметрической эконометрики: воспроизводимый подход с использованием R . Издательство Кембриджского университета. ISBN  9781108483407 .
• Симонов, Джеффри С. (1996). Методы сглаживания в статистике . Спрингер. ISBN  0-387-94716-7 .

Внешние ссылки

• Масштабно-адаптивная регрессия ядра (с программным обеспечением Matlab).
• Учебное пособие по регрессии ядра с использованием электронной таблицы (с Microsoft Excel ).
• Онлайн-демонстрация регрессии ядра . Требуется .NET 3.0 или более поздняя версия.
• Регрессия ядра с автоматическим выбором полосы пропускания (с Python)