Каталонская поверхность

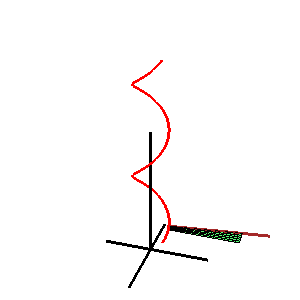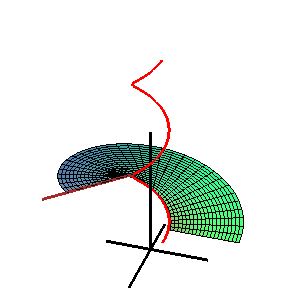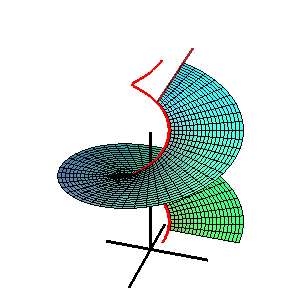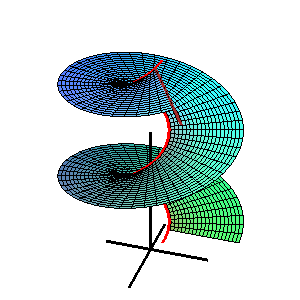
В геометрии , каталонская поверхность названная в честь бельгийского математика Эжена Шарля Каталана , представляет собой линейчатую поверхность, все образующие которой параллельны фиксированной плоскости .

Уравнения

Векторное уравнение каталонской поверхности имеет вид

р знак равно s ( ты ) + v L ( ты ),

где r = s ( u ) — пространственная кривая, а L ( u ) — единичный вектор правила в точке u = u . Все векторы L ( u ) параллельны одной плоскости, называемой направляющей плоскостью поверхности. Это можно охарактеризовать условием: смешанный продукт [ L ( u ), L' ( u ), L" ( u )] = 0. [1]

Параметрические уравнения каталонской поверхности имеют вид [2]

$x=f(u)+vi(u),\quad y=g(u)+vj(u),\quad z=h(u)+vk(u)\,$

Особые случаи

Если все образующие каталонской поверхности пересекают фиксированную прямую , то поверхность называется коноидом .

Каталан доказал, что геликоид и плоскость являются единственными линейчатыми минимальными поверхностями .

См. также

Обобщенный геликоид

Ссылки

А. Грей, Э. Аббена, С. Саламон, Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica , 3-е изд. Бока-Ратон, Флорида: CRC Press, 2006. [3] ( ISBN 978-1-58488-448-4 )
«Каталонская поверхность» , Математическая энциклопедия , EMS Press , 2001 [1994]
В.Я. Ровенский, Геометрия кривых и поверхностей с помощью MAPLE [4] ( ISBN 978-0-8176-4074-3 )