Обобщенный геликоид
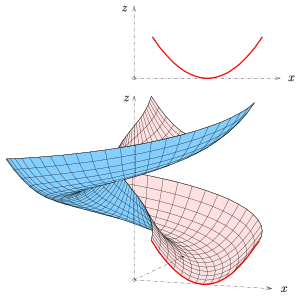
В геометрии обобщенный геликоид — это поверхность в евклидовом пространстве, образованная вращением и одновременным смещением кривой — профильной кривой — вдоль прямой, ее оси . Любая точка данной кривой является началом круговой спирали . Если кривая профиля содержится в плоскости, проходящей через ось, ее называют меридианом обобщенного геликоида. Простыми примерами обобщенных геликоидов являются геликоиды . Меридиан геликоида — это линия, пересекающая ось ортогонально.
Основными типами обобщенных геликоидов являются
- правили обобщенными геликоидами . Их кривые профиля представляют собой линии, а поверхности — линейчатые поверхности .
- круговые обобщенные геликоиды . Их кривые профиля представляют собой круги.
В математике геликоиды играют существенную роль как минимальные поверхности .В технической области обобщенные геликоиды используются для лестниц, направляющих, винтов и труб.
Аналитическое представление
[ редактировать ]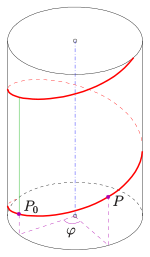
зеленый: смола,
синий: винтовая ось
Винтовое движение точки
[ редактировать ]Перемещение точки на винтовой кривой означает, что точка вращается и смещается вдоль линии (оси) так, что смещение пропорционально углу поворота. В результате получается круглая спираль .
Если осью является ось z , движение точки можно описать параметрически как
называется наклоном , угол , измеряемый в радианах, называется углом винта , а поле ( зеленое). След точки представляет собой круглую спираль (красный). Он содержится в поверхности прямого кругового цилиндра . Его радиус - это расстояние до точки к оси z .
В случае спираль называется правой ; в противном случае его называют левым .(В случае движение представляет собой вращение вокруг оси z .)
Винтовое движение кривой
[ редактировать ]Винтовое движение кривой
дает обобщенный геликоид с параметрическим представлением
Кривые представляют собой круговые спирали.
Кривые являются копиями заданной профильной кривой.
Пример: на первом рисунке выше меридиан представляет собой параболу .
Правильные обобщенные геликоиды
[ редактировать ]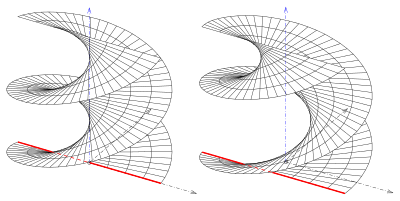
Типы
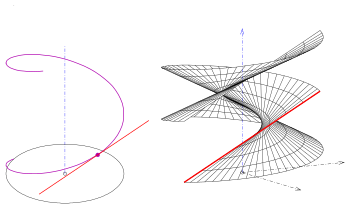
[ редактировать ]Если кривая профиля представляет собой прямую, получается линейчатый обобщенный геликоид . Существует четыре типа:
- (1) Линия пересекает ось ортогонально. Получается геликоид ( замкнутый обобщенный геликоид с правыми линейками).
- (2) Линия пересекает ось, но не ортогонально. Получается косой закрытый тип.
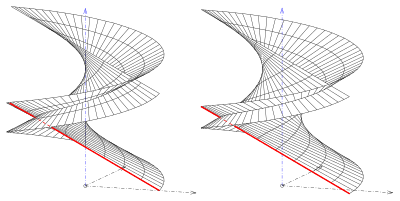
Если данная линия и ось являются косыми линиями, то получается открытый тип и ось не является частью поверхности (см. рисунок).
- (3) Если данная линия и ось являются косыми линиями и линия содержится в плоскости, ортогональной оси, то получается праворазомкнутый геликоид или короткозамкнутый геликоид .
- (4) Если линия и ось перекошены и линия не содержится в ... (п. 3), то получается косой открытый тип.
Наклонные типы пересекаются друг с другом (см. рисунок), а правильные типы (геликоиды) — нет.
Интересный случай получается, если линия наклонена к оси и произведению ее расстояния относительно оси и его наклон равен точно . В этом случае поверхность является касательной развертывающейся поверхностью и порождается директрисой .
Примечание:
- Геликоиды (открытые и закрытые) представляют собой каталонские поверхности . Закрытый тип (общий геликоид) представляет собой даже коноид.
- Линейчатые обобщенные геликоиды не являются алгебраическими поверхностями.
О замкнутых линейчатых обобщенных геликоидах
[ редактировать ]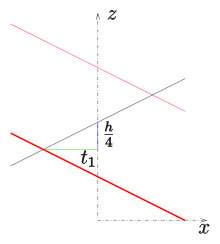
Замкнутый линейчатый обобщенный геликоид имеет линию профиля, пересекающую ось. Если линия профиля описывается получается следующее параметрическое представление
Если (общий геликоид) поверхность не пересекает сама себя.
Если (наклонный тип) поверхность пересекает саму себя и кривые (на поверхности)
- с
состоят из двойных точек . Существуют бесконечные двойные кривые. Чем меньше тем больше расстояния между двойными кривыми.
По касательному развертывающемуся типу
[ редактировать ]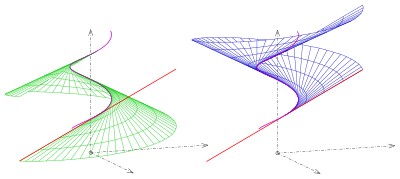
Для директрисы (спирали)
получаем следующее параметрическое представление касательной развертывающейся поверхности:
Вектор нормали к поверхности равен
Для нормальный вектор - это нулевой вектор. Следовательно, директриса состоит из особых точек. Директриса разделяет две регулярные части поверхности (см. рисунок).
Круговые обобщенные геликоиды
[ редактировать ]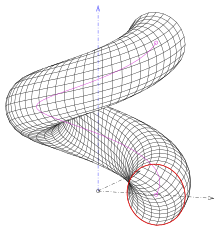
Существует 3 интересных типа круговых обобщенных геликоидов:
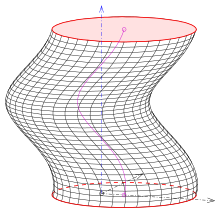
- (1) Если окружность является меридианом и не пересекает ось (см. рисунок).
- (2) Плоскость, содержащая окружность, ортогональна спирали центров окружностей. Получаем поверхность трубы
- (3) Плоскость окружности ортогональна оси и содержит в себе точку оси (см. рисунок). Этот тип использовался для колонн в стиле барокко.
- лестница, Университет Мангейма, Германия
- горка для труб Salinarium
- алтарь (1688 г.), Св. Панкратий, Нойенфельде, Германия
См. также
[ редактировать ]- геликоид
- Минимальная поверхность
- спираль
- Линейчатая поверхность
- Каталонская поверхность
- Коноид
- Поверхность революции
Внешние ссылки
[ редактировать ]- Гфреррер: Кривые и поверхности , стр. 47.
- mathcurve.com: круговой обобщенный геликоид
- mathcurve.com: развивающийся обобщенный геликоид
- mathcurve.com: линейчатый обобщенный геликоид
- K3Dsurf: генератор 3D-поверхностей
Ссылки
[ редактировать ]- Эльза Аббена, Саймон Саламон, Альфред Грей: Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica , 3-е издание, Исследования по высшей математике, Chapman & Hall, 2006, ISBN 1584884487 , с. 470
- Э. Крейциг: Дифференциальная геометрия . Нью-Йорк: Дувр, с. 88, 1991.
- У. Граф, М. Барнер: Начертательная геометрия. Квелле и Мейер, Гейдельберг, 1961 г., ISBN 3-494-00488-9 , стр.218.
- К. Штрубекер: Лекции по начертательной геометрии , Ванденхук и Рупрехт, Геттинген, 1967, с. 286




























