Исправление изображения

Исправление изображения — это процесс преобразования, используемый для проецирования изображений на общую плоскость изображения. Этот процесс имеет несколько степеней свободы и существует множество стратегий преобразования изображений в общую плоскость. Исправление изображений используется в компьютерном стереозрении для упрощения задачи поиска точек совпадения между изображениями (т. е. проблемы соответствия ), а также в географических информационных системах (ГИС) для объединения изображений, снятых с нескольких точек зрения, в общую систему координат карты.

В компьютерном зрении

Компьютерное стереозрение позволяет получить два или более изображений с известными относительными положениями камеры, на которых объект показан с разных точек зрения. Затем для каждого пикселя он определяет глубину соответствующей точки сцены (т. е. расстояние от камеры), сначала находя совпадающие пиксели (т. е. пиксели, показывающие одну и ту же точку сцены) на другом изображении(ях), а затем применяя триангуляцию к найденным совпадениям, чтобы определить их глубина.Поиск совпадений в стереозрении ограничен эпиполярной геометрией : совпадение каждого пикселя на другом изображении можно найти только на линии, называемой эпиполярной линией.Если два изображения копланарны, то есть они были сняты так, что правая камера смещена только по горизонтали по сравнению с левой камерой (не перемещается к объекту и не вращается), то эпиполярная линия каждого пикселя горизонтальна и находится в том же вертикальном положении, что и эта. пиксель. Однако в общих настройках (камера движется к объекту или вращается) эпиполярные линии наклонены. Исправление изображения искажает оба изображения так, что они выглядят так, как будто они были сняты только с горизонтальным смещением, и, как следствие, все эпиполярные линии становятся горизонтальными, что немного упрощает процесс сопоставления стерео. Однако обратите внимание, что исправление не меняет фундаментально процесс сопоставления стерео: поиск выполняется по линиям, наклонным до и горизонтальным после исправления.

Исправление изображения также является эквивалентом (и чаще используется ^[1]) альтернатива идеальной компланарности камеры. Даже при использовании высокоточного оборудования обычно выполняется исправление изображения, поскольку поддерживать идеальную копланарность между камерами может быть непрактично.

Исправление изображения может выполняться только с двумя изображениями одновременно, а одновременное исправление более двух изображений обычно невозможно. ^[2]

Трансформация

Если изображения, подлежащие исправлению, взяты с пар камер без геометрических искажений , этот расчет можно легко выполнить с помощью линейного преобразования . Вращение по X и Y помещает изображения в одну плоскость, масштабирование делает кадры изображения одинакового размера, а вращение и наклон по оси Z выравнивают ряды пикселей изображения. ^{[ нужна ссылка ]}. Необходимо знать жесткое выравнивание камер (путем калибровки), а коэффициенты калибровки используются при преобразовании. ^[3]

При выполнении преобразования, если сами камеры калибруются по внутренним параметрам, необходимая матрица обеспечивает взаимосвязь между камерами. Более общий случай (без калибровки камеры) представлен фундаментальной матрицей . Если фундаментальная матрица неизвестна, необходимо найти предварительные точечные соответствия между стереоизображениями для облегчения ее извлечения. ^[3]

Алгоритмы

Существует три основные категории алгоритмов исправления изображения: планарное исправление, ^[4] цилиндрический выпрямитель ^[1] и полярное выпрямление. ^[5]^[6]^[7]

Детали реализации

Все исправленные изображения удовлетворяют следующим двум свойствам: ^[8]

Все эпиполярные линии параллельны горизонтальной оси.
Соответствующие точки имеют одинаковые вертикальные координаты.

Чтобы преобразовать исходную пару изображений в выпрямленную пару изображений, необходимо найти проективное преобразование H . накладываются ограничения На H для удовлетворения двух вышеуказанных свойств. Например, ограничение параллельности эпиполярных линий горизонтальной оси означает, что эпиполи должны быть сопоставлены с бесконечной точкой [1,0,0] ^Т в однородных координатах . Даже с учетом этих ограничений H по-прежнему имеет четыре степени свободы. ^[9] Также необходимо найти соответствующий H', чтобы исправить второе изображение пары изображений. Неправильный выбор H и H' может привести к тому, что исправленные изображения будут резко изменены в масштабе или сильно искажены.

Существует множество различных стратегий выбора проективного преобразования H для каждого изображения из всех возможных решений. Одним из продвинутых методов является минимизация несоответствия или разницы по методу наименьших квадратов соответствующих точек на горизонтальной оси пары выпрямленных изображений. ^[9] Другой метод — разделение H на специализированное проективное преобразование, преобразование подобия и преобразование сдвига, чтобы минимизировать искажение изображения. ^[8] Один простой метод — повернуть оба изображения так, чтобы они выглядели перпендикулярно линии, соединяющей их общие оптические центры, повернуть оптические оси так, чтобы горизонтальная ось каждого изображения указывала в направлении оптического центра другого изображения, и, наконец, масштабировать меньшее изображение, чтобы оно соответствовало для прямой переписки. ^[2] Этот процесс продемонстрирован в следующем примере.

Пример

Набор 2D изображений из примера. Исходные изображения сделаны с разных ракурсов (ряд 1). Используя систематические преобразования из примера (строки 2 и 3), мы можем преобразовать оба изображения так, чтобы соответствующие точки находились на одних и тех же линиях горизонтального сканирования (строка 4).

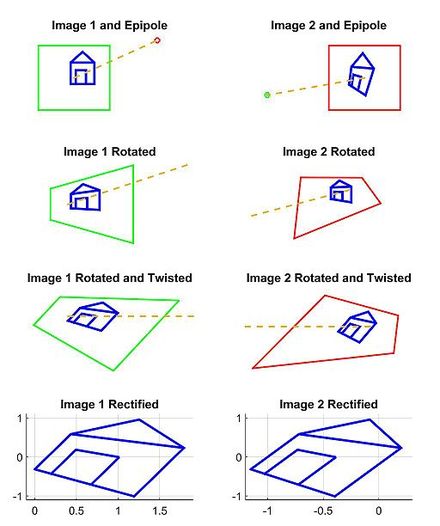
Наша модель для этого примера основана на паре изображений, на которых наблюдается трехмерная точка P , которая соответствует p и p' в координатах пикселей каждого изображения. O и O' представляют собой оптические центры каждой камеры с известными матрицами камер. $M=K[I~0]$ и $M'=K'[R~T]$ (мы предполагаем, что начало координат находится в первой камере). Мы кратко опишем и изобразим результаты простого подхода к поиску проективного преобразования H и H ', которое исправляет пару изображений из примера сцены.

Сначала мы вычисляем эпиполи e и e' на каждом изображении:

e=M{\begin{bmatrix}O'\\1\end{bmatrix}}=M{\begin{bmatrix}-R^{T}T\\1\end{bmatrix}}=K[I~0]{\begin{bmatrix}-R^{T}T\\1\end{bmatrix}}=-KR^{T}T

e'=M'{\begin{bmatrix}O\\1\end{bmatrix}}=M'{\begin{bmatrix}0\\1\end{bmatrix}}=K'[R~T]{\begin{bmatrix}0\\1\end{bmatrix}}=K'T

Во-вторых, мы находим проективное преобразование H ₁ , которое поворачивает наше первое изображение так, чтобы оно было параллельно базовой линии, соединяющей O и O' (строка 2, столбец 1 набора двумерных изображений). Это вращение можно найти, используя векторное произведение исходной и желаемой оптических осей. ^[2] Далее мы находим проективное преобразование H ₂ , которое берет повернутое изображение и поворачивает его так, чтобы горизонтальная ось совпадала с базовой линией. Если рассчитано правильно, это второе преобразование должно сопоставить e с бесконечностью по оси x (строка 3, столбец 1 набора 2D-изображений). Наконец, определите $H=H_{2}H_{1}$ как проективное преобразование для исправления первого образа.

В-третьих, с помощью эквивалентной операции мы можем найти H' , чтобы исправить второе изображение (столбец 2 набора 2D-изображений). Обратите внимание, что H' ₁ должен повернуть оптическую ось второго изображения так, чтобы она была параллельна преобразованной оптической оси первого изображения. Одна из стратегий — выбрать плоскость, параллельную линии пересечения двух исходных оптических осей, чтобы минимизировать искажения, возникающие в процессе перепроецирования. ^[10] В этом примере мы просто определяем H', используя матрицу вращения R и начальное проективное преобразование H как $H'=HR^{T}$ .

Наконец, мы масштабируем оба изображения до одинакового приблизительного разрешения и выравниваем теперь горизонтальные эпиполи для облегчения горизонтального сканирования на предмет соответствий (строка 4 набора 2D-изображений).

Обратите внимание, что этот и подобные алгоритмы можно выполнить, не имея матриц параметров камеры M и M' . Все, что требуется, — это набор из семи или более соответствий изображений для вычисления фундаментальных матриц и эпиполей. ^[9]

В геоинформационной системе

Исправление изображений в ГИС преобразует изображения в стандартную систему координат карты. Это делается путем сопоставления наземных опорных точек (GCP) в картографической системе с точками на изображении. Эти GCP рассчитывают необходимые преобразования изображения. ^[11]

Основные трудности в процессе возникают

когда точность точек карты неизвестна
когда на изображениях отсутствуют четко идентифицируемые точки, соответствующие картам.

Карты, используемые с исправленными изображениями, не являются топографическими. Однако используемые изображения могут содержать искажения местности. Ортотрансформация изображения дополнительно устраняет эти эффекты. ^[11]

Исправление изображений — стандартная функция, доступная в пакетах программного обеспечения ГИС.

См. также

Ссылки

^ Jump up to: ^а ^б Орам, Дэниел (2001). Ректификация для любой эпиполярной геометрии .
^ Jump up to: ^а ^б ^с Селиски, Ричард (2010). Компьютерное зрение: Алгоритмы и приложения . Спрингер. ISBN 9781848829350 .
^ Jump up to: ^а ^б Фузиелло, Андреа (17 марта 2000 г.). «Эпиполярная ректификация» . Архивировано из оригинала 13 ноября 2015 г. Проверено 9 июня 2008 г.
^ Фузиелло, Андреа; Трукко, Эмануэле; Верри, Алессандро (2 марта 2000 г.). «Компактный алгоритм исправления стереопар» (PDF) . Машинное зрение и его приложения . 12 :16–22. дои : 10.1007/s001380050120 . S2CID 13250851 . Архивировано из оригинала (PDF) 23 сентября 2015 г. Проверено 8 июня 2010 г.
^ Поллефейс, Марк; Кох, Рейнхард; Ван Гул, Люк (1999). «Простой и эффективный метод исправления общего движения» (PDF) . Учеб. Международная конференция по компьютерному зрению : 496–501 . Проверено 19 января 2011 г.
^ Лим, Сер-Нам; Миттал, Анураг; Дэвис, Ларри; Парагиос, Никос. «Некалиброванное стереоисправление для автоматического 3D-наблюдения» (PDF) . Международная конференция по обработке изображений . 2 : 1357. Архивировано из оригинала (PDF) 21 августа 2010 г. Проверено 8 июня 2010 г.
^ Роберто, Рафаэль; Тейхриб, Вероника; Келнер, Джудит (2009). «Цилиндрическое выпрямление: эффективный метод исправления пары изображений» (PDF) . Мастер-классы Сибграпи 2009 – Бакалаврские работы (на португальском языке). Архивировано из оригинала (PDF) 6 июля 2011 г. Проверено 5 марта 2011 г.
^ Jump up to: ^а ^б Луп, Чарльз; Чжан, Чжэнъю (1999). «Вычисление исправления гомографий для стереозрения» (PDF) . Слушания. 1999 г. Конференция IEEE Computer Society по компьютерному зрению и распознаванию образов (кат. № PR00149) . стр. 125–131. CiteSeerX 10.1.1.34.6182 . дои : 10.1109/CVPR.1999.786928 . ISBN 978-0-7695-0149-9 . S2CID 157172 . Проверено 9 ноября 2014 г.
^ Jump up to: ^а ^б ^с Хартли, Ричард; Зиссерман, Эндрю (2003). Многовидовая геометрия в компьютерном зрении . Издательство Кембриджского университета. ISBN 9780521540513 .
^ Форсайт, Дэвид А.; Понсе, Жан (2002). Компьютерное зрение: современный подход . Профессиональный технический справочник Прентис Холл.
^ Jump up to: ^а ^б Фогель, Дэвид. «Исправление изображения с помощью радиальных базисных функций» . Архивировано из оригинала 24 мая 2008 г. Проверено 9 июня 2008 г.

Хартли, Род-Айленд (1999). «Теория и практика проективной ректификации». Международный журнал компьютерного зрения . 35 (2): 115–127. дои : 10.1023/А:1008115206617 . S2CID 406463 .
Поллефейс, Марк. «Полярное выпрямление» . Проверено 9 июня 2007 г.
Шапиро, Линда Г .; Стокман, Джордж К. (2001). Компьютерное зрение . Прентис Холл. стр. 580 . ISBN 978-0-13-030796-5 .

Дальнейшее чтение

Вычисление выпрямляющих гомографий для стереозрения Чарльза Лупа и Чжэнъю Чжана (8 апреля 1999 г.) Microsoft Research
Компьютерное зрение: алгоритмы и приложения, раздел 11.1.1 «Исправление», Ричард Селиски (3 сентября 2010 г.) Springer

[ORAM2001-1] Jump up to: ^а ^б Орам, Дэниел (2001). Ректификация для любой эпиполярной геометрии .

[SZELISKI2010-2] Jump up to: ^а ^б ^с Селиски, Ричард (2010). Компьютерное зрение: Алгоритмы и приложения . Спрингер. ISBN 9781848829350 .

[FUSIELLO2000-3] Jump up to: ^а ^б Фузиелло, Андреа (17 марта 2000 г.). «Эпиполярная ректификация» . Архивировано из оригинала 13 ноября 2015 г. Проверено 9 июня 2008 г.

[FUSIELLO2000_2-4] Фузиелло, Андреа; Трукко, Эмануэле; Верри, Алессандро (2 марта 2000 г.). «Компактный алгоритм исправления стереопар» (PDF) . Машинное зрение и его приложения . 12 :16–22. дои : 10.1007/s001380050120 . S2CID 13250851 . Архивировано из оригинала (PDF) 23 сентября 2015 г. Проверено 8 июня 2010 г.

[POLLEFEYS1999-5] Поллефейс, Марк; Кох, Рейнхард; Ван Гул, Люк (1999). «Простой и эффективный метод исправления общего движения» (PDF) . Учеб. Международная конференция по компьютерному зрению : 496–501 . Проверено 19 января 2011 г.

[LIM2004-6] Лим, Сер-Нам; Миттал, Анураг; Дэвис, Ларри; Парагиос, Никос. «Некалиброванное стереоисправление для автоматического 3D-наблюдения» (PDF) . Международная конференция по обработке изображений . 2 : 1357. Архивировано из оригинала (PDF) 21 августа 2010 г. Проверено 8 июня 2010 г.

[ROBERTO2009-7] Роберто, Рафаэль; Тейхриб, Вероника; Келнер, Джудит (2009). «Цилиндрическое выпрямление: эффективный метод исправления пары изображений» (PDF) . Мастер-классы Сибграпи 2009 – Бакалаврские работы (на португальском языке). Архивировано из оригинала (PDF) 6 июля 2011 г. Проверено 5 марта 2011 г.

[ZHANG2009-8] Jump up to: ^а ^б Луп, Чарльз; Чжан, Чжэнъю (1999). «Вычисление исправления гомографий для стереозрения» (PDF) . Слушания. 1999 г. Конференция IEEE Computer Society по компьютерному зрению и распознаванию образов (кат. № PR00149) . стр. 125–131. CiteSeerX 10.1.1.34.6182 . дои : 10.1109/CVPR.1999.786928 . ISBN 978-0-7695-0149-9 . S2CID 157172 . Проверено 9 ноября 2014 г.

[HARTLEY2003-9] Jump up to: ^а ^б ^с Хартли, Ричард; Зиссерман, Эндрю (2003). Многовидовая геометрия в компьютерном зрении . Издательство Кембриджского университета. ISBN 9780521540513 .

[FORSYTH2002-10] Форсайт, Дэвид А.; Понсе, Жан (2002). Компьютерное зрение: современный подход . Профессиональный технический справочник Прентис Холл.

[FOGEL2008-11] Jump up to: ^а ^б Фогель, Дэвид. «Исправление изображения с помощью радиальных базисных функций» . Архивировано из оригинала 24 мая 2008 г. Проверено 9 июня 2008 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]