Кактус граф

В теории графов кактус , (иногда называемый кактусовым деревом ) — это связный граф в котором любые два простых цикла имеют не более одной вершины общей . Эквивалентно, это связный граф, в котором каждое ребро принадлежит не более чем одному простому циклу или (для нетривиальных кактусов) в котором каждый блок (максимальный подграф без разрезной вершины ) является ребром или циклом.

Характеристики

Кактусы — это внешнепланарные графы . Каждое псевдодерево — это кактус. Нетривиальный граф является кактусом тогда и только тогда, когда каждый блок представляет собой либо простой цикл , либо одно ребро.

Семейство графов, в котором каждый компонент является кактусом, замкнуто сверху вниз относительно второстепенных операций над графом. Это семейство графов можно охарактеризовать одним запрещенным минором с четырьмя вершинами, — ромбовидным графом образованным удалением ребра из полного графа K ₄ . ^[1]

Треугольный кактус

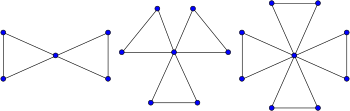
Треугольный кактус — это особый тип графа кактуса, в котором каждый цикл имеет длину три и каждое ребро принадлежит циклу. Например, графы дружбы , графы, образованные из набора треугольников, соединенных вместе в одной общей вершине, представляют собой треугольные кактусы. Помимо того, что треугольные кактусы являются графами-кактусами, они также являются блочными графами и локально линейными графами .

Треугольные кактусы обладают тем свойством, что они остаются соединенными, если какое-либо соответствие из них удалить ; для заданного числа вершин они имеют наименьшее количество ребер с этим свойством. Любое дерево с нечетным числом вершин можно дополнить до треугольного кактуса, добавив к нему ребра. дающее минимальное дополнение со свойством оставаться связным после удаления паросочетания. ^[2]

Самый большой треугольный кактус в любом графе можно найти за полиномиальное время, используя алгоритм задачи четности матроидов . Поскольку треугольные графы кактусов являются плоскими графами , самый большой треугольный кактус можно использовать как приближение к самому большому планарному подграфу, что является важной подзадачой планаризации . В качестве алгоритма аппроксимации этот метод имеет коэффициент аппроксимации 4/9, наиболее известный для задачи о максимальном плоском подграфе. ^[3]

Алгоритм поиска самого большого треугольного кактуса связан с теоремой Ловаса и Пламмера, характеризующей количество треугольников в этом самом большом кактусе. ^[4]Ловас и Пламмер рассматривают пары разбиений вершин и ребер данного графа на подмножества со свойством, что каждый треугольник графа либо имеет две вершины в одном классе разбиения вершин, либо все три ребра в одном классе разбиения вершин. краевая перегородка; они называют пару разделов с этим свойством валидной .Тогда количество треугольников в самом большом треугольном кактусе равно максимальному по парам допустимых разбиений. ${\mathcal {P}}=\{V_{1},V_{2},\dots ,V_{k}\}$ и ${\mathcal {Q}}=\{E_{1},E_{2},\dots ,E_{m}\}$ , из

\sum _{i=1}^{m}{\frac {(u_{i}-1)}{2}}+n-k,

,

где $n$ - количество вершин в данном графе и $u_{i}$ количество классов вершин, которым соответствует класс ребра $E_{i}$ .

Каждый плоский граф $G$ содержит подграф кактуса $C\subseteq G$ который включает в себя как минимум $1/6$ часть треугольных граней $G$ . Этот результат подразумевает прямой анализ алгоритма 4/9-аппроксимации для задачи о максимально плоском подграфе без использования приведенной выше формулы min-max. ^[5]

Гипотеза Розы

Важной гипотезой, связанной с треугольным кактусом, является гипотеза Розы , названная в честь Александра Розы , которая гласит, что все треугольные кактусы изящны или почти изящны. ^[6] Точнее

Все треугольные кактусы с блоками t ≡ 0, 1 mod 4 изящны, а с t ≡ 2, 3 mod 4 почти изящны.

Алгоритмы и приложения

Некоторые задачи размещения объектов, которые являются NP-сложными для общих графов, а также некоторые другие проблемы графов, могут быть решены за полиномиальное время для кактусов. ^[7]^[8]

Поскольку кактусы являются частным случаем внешнепланарных графов , ряд задач комбинаторной оптимизации графов может быть решен для них за полиномиальное время . ^[9]

Кактусы представляют собой электрические цепи , обладающие полезными свойствами. Раннее применение кактусов было связано с представлением операционных усилителей. ^[10]^[11]^[12]

Кактусы также использовались в сравнительной геномике как способ представления взаимосвязей между различными геномами или частями геномов. ^[13]

Если кактус связный, и каждая его вершина принадлежит не более чем двум блокам, то он называется рождественским кактусом . Каждый многогранный граф имеет подграф рождественского кактуса, который включает в себя все его вершины, и этот факт играет важную роль в доказательстве Лейтона и Мойтры (2010) , что каждый многогранный граф имеет жадное вложение в евклидову плоскость , присвоение координат вершины, для которых жадная пересылка успешно перенаправляет сообщения между всеми парами вершин. ^[14]

В топологической теории графов графы, клеточные вложения все которых плоские, представляют собой в точности подсемейство графов-кактусов с дополнительным свойством, согласно которому каждая вершина принадлежит не более чем одному циклу. Эти графы имеют два запрещенных минора: ромбовидный граф и пятивершинный граф дружбы . ^[15]

История

Кактусы впервые были изучены под названием « деревья Хусими» , дарованные им Фрэнком Харари и Джорджем Юджином Уленбеком в честь предыдущей работы над этими графиками Коди Хусими . ^[16]^[17] В той же статье Харари-Уленбека за графами этого типа, в которых каждый цикл представляет собой треугольник, зарезервировано название «кактус», но теперь стандартом является разрешение циклов любой длины.

Между тем, название « дерево Хусими» обычно относилось к графам, в которых каждый блок представляет собой полный граф (что эквивалентно графам пересечения блоков в каком-либо другом графе). Такое использование не имело ничего общего с работой Хусими, и более подходящий термин «график блоков» теперь для этого семейства используется ; однако из-за этой двусмысленности эта фраза стала реже использоваться для обозначения графов кактусов. ^[18]

Ссылки

^ Эль-Маллах, Эхаб; Колборн, Чарльз Дж. (1988), «Сложность некоторых проблем с удалением ребер», IEEE Transactions on Circuits and Systems , 35 (3): 354–362, doi : 10.1109/31.1748
^ Фарли, Артур М.; Проскуровски, Анджей (1982), «Сети, невосприимчивые к отказам изолированных линий», Networks , 12 (4): 393–403, doi : 10.1002/net.3230120404 , MR 0686540
^ Кэлинеску, Груя; Фернандес, Кристина Дж; Финклер, Ульрих; Карлофф, Ховард (2002), «Алгоритм лучшего приближения для поиска плоских подграфов», Journal of Algorithms , 2, 27 (2): 269–302, CiteSeerX 10.1.1.47.4731 , doi : 10.1006/jagm.1997.0920 , S2CID 8329680
^ Ловас, Л. ; Пламмер, доктор медицины (2009), Теория соответствия , издательская серия AMS Chelsea, ISBN 9780821847596
^ Чалермсук, Паринья; Шмид, Андреас; Униял, Сумедха (2019), «Точная экстремальная граница числа кактусов Ловаса в плоских графах», у Нидермайера, Рольфа; Пол, Кристоф (ред.), 36-й Международный симпозиум по теоретическим аспектам информатики, STACS 2019, 13–16 марта 2019 г., Берлин, Германия , LIPics, vol. 126, Schloss Dagstuhl - Центр компьютерных наук Лейбница, стр. 19: 1–19: 14, arXiv : 1804.03485 , doi : 10.4230/LIPIcs.STACS.2019.19 , ISBN 9783959771009 , S2CID 4751972
^ Роза, А. (1988), «Циклические тройные системы Штейнера и маркировка треугольных кактусов», Scientia , 1 : 87–95 .
^ Бен-Моше, Воаз; Бхаттачарья, Бинай; Ши, Цяошэн (2005), «Эффективные алгоритмы для решения взвешенной задачи двух центров в графе кактуса», Алгоритмы и вычисления, 16-й международный форум. Symp., ISAAC 2005 , Конспекты лекций по информатике , том. 3827, Springer-Verlag, стр. 693–703, номер документа : 10.1007/11602613_70 , ISBN. 978-3-540-30935-2
^ Змазек, Блаз; Зеровник, Янез (2005), «Оценка трафика во взвешенных сетях кактусов в линейном времени», Девятая Международная конференция по визуализации информации (IV'05) , стр. 536–541, doi : 10.1109/IV.2005.48 , ISBN 978-0-7695-2397-2 , S2CID 15963409
^ Корнеенко, Н. М. (1994), «Комбинаторные алгоритмы на одном классе графов», Дискретная прикладная математика , 54 (2–3): 215–217, doi : 10.1016/0166-218X(94)90022-1 . Перевод из «Извещений АН БССР», сер. Физ.-матем. наук. , (1984) нет. 3, стр. 109-111 (на русском языке)
^ Ниси, Тецуо; Чуа, Леон О. (1986), «Топологическое доказательство теоремы Нильсена-Уилсона», IEEE Transactions on Circuits and Systems , 33 (4): 398–405, doi : 10.1109/TCS.1986.1085935
^ Ниси, Тецуо; Чуа, Леон О. (1986), «Единственность решения для нелинейных резистивных цепей, содержащих CCCS или VCVS, управляющие коэффициенты которых конечны», IEEE Transactions on Circuits and Systems , 33 (4): 381–397, doi : 10.1109/TCS. 1986.1085934
^ Ниши, Тецуо (1991), «О количестве решений класса нелинейных резистивных цепей», Труды Международного симпозиума IEEE по схемам и системам, Сингапур , стр. 766–769.
^ Патен, Бенедикт; Диканс, Марк; Эрл, Дент; Сент-Джон, Джон; Ма, Цзянь; Ох, Бернард; Хаусслер, Дэвид (2010), «Кактусовые графики для сравнения геномов» , Исследования в области вычислительной молекулярной биологии , Конспекты лекций по информатике, том. 6044, стр. 410–425 , doi : 10.1007/978-3-642-12683-3_27 , ISBN. 978-3-642-12682-6
^ Лейтон, Том ; Мойтра, Анкур (2010), «Некоторые результаты по жадным вложениям в метрические пространства» (PDF) , Discrete & Computational Geometry , 44 (3): 686–705, doi : 10.1007/s00454-009-9227-6 , S2CID 11186402 .
^ Нордхаус, Э.А.; Рингейзен, РД; Стюарт, Б.М.; Уайт, А.Т. (1972), «Теорема типа Куратовского для максимального рода графа», Журнал комбинаторной теории , серия B, 12 (3): 260–267, doi : 10.1016/0095-8956(72)90040 -8 , МР 0299523
^ Харари, Фрэнк ; Уленбек, Джордж Э. (1953), «О количестве деревьев Хусими, I», Proceedings of the National Academy of Sciences , 39 (4): 315–322, Бибкод : 1953PNAS...39..315H , doi : 10.1073/pnas.39.4.315 , MR 0053893 , PMC 1063779 , PMID 16589268
^ Хусими, Коди (1950), «Заметки о теории кластерных интегралов Майерса», Journal of Chemical Physics , 18 (5): 682–684, Bibcode : 1950JChPh..18..682H , doi : 10.1063/1.1747725 , MR 0038903
^ См., например, MR. 0659742 , обзор Роберта Э. Джеймисона 1983 года на статью, использующую другое определение, которое приписывает двусмысленность ошибке в книге Мехди Бехзада и Гэри Чартранда .

Внешние ссылки

Применение кактусовых графов при анализе и проектировании электронных схем

[1] Эль-Маллах, Эхаб; Колборн, Чарльз Дж. (1988), «Сложность некоторых проблем с удалением ребер», IEEE Transactions on Circuits and Systems , 35 (3): 354–362, doi : 10.1109/31.1748

[2] Фарли, Артур М.; Проскуровски, Анджей (1982), «Сети, невосприимчивые к отказам изолированных линий», Networks , 12 (4): 393–403, doi : 10.1002/net.3230120404 , MR 0686540

[3] Кэлинеску, Груя; Фернандес, Кристина Дж; Финклер, Ульрих; Карлофф, Ховард (2002), «Алгоритм лучшего приближения для поиска плоских подграфов», Journal of Algorithms , 2, 27 (2): 269–302, CiteSeerX 10.1.1.47.4731 , doi : 10.1006/jagm.1997.0920 , S2CID 8329680

[4] Ловас, Л. ; Пламмер, доктор медицины (2009), Теория соответствия , издательская серия AMS Chelsea, ISBN 9780821847596

[5] Чалермсук, Паринья; Шмид, Андреас; Униял, Сумедха (2019), «Точная экстремальная граница числа кактусов Ловаса в плоских графах», у Нидермайера, Рольфа; Пол, Кристоф (ред.), 36-й Международный симпозиум по теоретическим аспектам информатики, STACS 2019, 13–16 марта 2019 г., Берлин, Германия , LIPics, vol. 126, Schloss Dagstuhl - Центр компьютерных наук Лейбница, стр. 19: 1–19: 14, arXiv : 1804.03485 , doi : 10.4230/LIPIcs.STACS.2019.19 , ISBN 9783959771009 , S2CID 4751972

[Rosa1988-6] Роза, А. (1988), «Циклические тройные системы Штейнера и маркировка треугольных кактусов», Scientia , 1 : 87–95 .

[7] Бен-Моше, Воаз; Бхаттачарья, Бинай; Ши, Цяошэн (2005), «Эффективные алгоритмы для решения взвешенной задачи двух центров в графе кактуса», Алгоритмы и вычисления, 16-й международный форум. Symp., ISAAC 2005 , Конспекты лекций по информатике , том. 3827, Springer-Verlag, стр. 693–703, номер документа : 10.1007/11602613_70 , ISBN. 978-3-540-30935-2

[8] Змазек, Блаз; Зеровник, Янез (2005), «Оценка трафика во взвешенных сетях кактусов в линейном времени», Девятая Международная конференция по визуализации информации (IV'05) , стр. 536–541, doi : 10.1109/IV.2005.48 , ISBN 978-0-7695-2397-2 , S2CID 15963409

[9] Корнеенко, Н. М. (1994), «Комбинаторные алгоритмы на одном классе графов», Дискретная прикладная математика , 54 (2–3): 215–217, doi : 10.1016/0166-218X(94)90022-1 . Перевод из «Извещений АН БССР», сер. Физ.-матем. наук. , (1984) нет. 3, стр. 109-111 (на русском языке)

[10] Ниси, Тецуо; Чуа, Леон О. (1986), «Топологическое доказательство теоремы Нильсена-Уилсона», IEEE Transactions on Circuits and Systems , 33 (4): 398–405, doi : 10.1109/TCS.1986.1085935

[11] Ниси, Тецуо; Чуа, Леон О. (1986), «Единственность решения для нелинейных резистивных цепей, содержащих CCCS или VCVS, управляющие коэффициенты которых конечны», IEEE Transactions on Circuits and Systems , 33 (4): 381–397, doi : 10.1109/TCS. 1986.1085934

[12] Ниши, Тецуо (1991), «О количестве решений класса нелинейных резистивных цепей», Труды Международного симпозиума IEEE по схемам и системам, Сингапур , стр. 766–769.

[13] Патен, Бенедикт; Диканс, Марк; Эрл, Дент; Сент-Джон, Джон; Ма, Цзянь; Ох, Бернард; Хаусслер, Дэвид (2010), «Кактусовые графики для сравнения геномов» , Исследования в области вычислительной молекулярной биологии , Конспекты лекций по информатике, том. 6044, стр. 410–425 , doi : 10.1007/978-3-642-12683-3_27 , ISBN. 978-3-642-12682-6

[14] Лейтон, Том ; Мойтра, Анкур (2010), «Некоторые результаты по жадным вложениям в метрические пространства» (PDF) , Discrete & Computational Geometry , 44 (3): 686–705, doi : 10.1007/s00454-009-9227-6 , S2CID 11186402 .

[15] Нордхаус, Э.А.; Рингейзен, РД; Стюарт, Б.М.; Уайт, А.Т. (1972), «Теорема типа Куратовского для максимального рода графа», Журнал комбинаторной теории , серия B, 12 (3): 260–267, doi : 10.1016/0095-8956(72)90040 -8 , МР 0299523

[16] Харари, Фрэнк ; Уленбек, Джордж Э. (1953), «О количестве деревьев Хусими, I», Proceedings of the National Academy of Sciences , 39 (4): 315–322, Бибкод : 1953PNAS...39..315H , doi : 10.1073/pnas.39.4.315 , MR 0053893 , PMC 1063779 , PMID 16589268

[17] Хусими, Коди (1950), «Заметки о теории кластерных интегралов Майерса», Journal of Chemical Physics , 18 (5): 682–684, Bibcode : 1950JChPh..18..682H , doi : 10.1063/1.1747725 , MR 0038903

[18] См., например, MR. 0659742 , обзор Роберта Э. Джеймисона 1983 года на статью, использующую другое определение, которое приписывает двусмысленность ошибке в книге Мехди Бехзада и Гэри Чартранда .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]