Однородность и неоднородность (статистика)
В статистике однородность неоднородность ее противоположность, и , возникают при описании свойств набора данных или нескольких наборов данных. Они связаны с обоснованностью зачастую удобного предположения о том, что статистические свойства любой части общего набора данных такие же, как и любой другой части. В метаанализе , который объединяет данные нескольких исследований, однородность измеряет различия или сходства между несколькими исследованиями (см. также «Разнородность исследования »).
Однородность можно изучать на нескольких степенях сложности. Например, соображения гомоскедастичности исследуют, насколько изменчивость значений данных меняется в наборе данных. Однако вопросы однородности применимы ко всем аспектам статистического распределения , включая параметр местоположения . Таким образом, более детальное исследование позволит изучить изменения во всем предельном распределении . Исследование промежуточного уровня может перейти от рассмотрения изменчивости к изучению изменений асимметрии . Помимо этого, вопросы однородности применимы и к совместному распределению .
Понятие однородности может применяться по-разному, и для определенных типов статистического анализа оно используется для поиска дополнительных свойств, которые, возможно, потребуется рассматривать как изменяющиеся в наборе данных после того, как будут рассмотрены некоторые начальные типы неоднородности. с.
дисперсии
[ редактировать ]
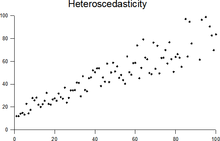
В статистике последовательность , является случайных величин гомоскедастической ( / ˌ h oʊ m oʊ s k ə ˈ d æ s t ɪ k / ) если все ее случайные величины имеют одинаковую конечную дисперсию ; это также известно как однородность дисперсии. Дополнительное понятие называется гетероскедастичностью, также известной как гетерогенность дисперсии. варианты написания гомоскедастичность и гетероскедастичность Также часто используются . Скедастичность происходит от древнегреческого слова skedánnymi, что означает «рассеивать». [1] [2] [3] Предположение, что переменная гомоскедастична, тогда как на самом деле она гетероскедастична ( / ˌ h ɛ t ər oʊ s k ə ˈ d æ s t ɪ k / ) приводит к несмещенным, но неэффективным точечным оценкам и к смещенным оценкам стандартных ошибок , и может привести к переоценка степени соответствия , измеряемой коэффициентом Пирсона .
Существование гетероскедастичности является серьезной проблемой в регрессионном анализе и дисперсионном анализе , поскольку оно делает недействительными статистические тесты значимости , которые предполагают, что все ошибки моделирования имеют одинаковую дисперсию. Хотя обычная оценка методом наименьших квадратов все еще является несмещенной при наличии гетероскедастичности, она неэффективна, а вывод, основанный на предположении о гомоскедастичности, вводит в заблуждение. В этом случае метод обобщенных наименьших квадратов (GLS). в прошлом часто использовался [4] [5] В настоящее время стандартной практикой в эконометрике является включение стандартных ошибок, согласованных с гетероскедастичностью , вместо использования GLS, поскольку GLS может демонстрировать сильную предвзятость в небольших выборках, если фактическая скедастическая функция неизвестна. [6]
Поскольку гетероскедастичность касается ожиданий второго момента ошибки, ее наличие называется некорректной спецификацией второго порядка. [7]
Эконометрист при наличии гетероскедастичности, которые привели к Роберт Энгл был удостоен Нобелевской премии по экономике 2003 года за исследования регрессионного анализа формулировке метода моделирования авторегрессионной условной гетероскедастичности (ARCH). [8]Примеры
[ редактировать ]Регрессия
[ редактировать ]Различия в типичных значениях в наборе данных первоначально можно устранить путем построения регрессионной модели с использованием определенных независимых переменных, чтобы связать изменения типичного значения с известными величинами. Затем должен быть проведен более поздний этап анализа, чтобы проверить, ведут ли ошибки в прогнозах регрессии одинаково во всем наборе данных. Таким образом, возникает вопрос об однородности распределения остатков по мере изменения объясняющих переменных. См. регрессионный анализ .
Временной ряд
[ редактировать ]Начальные этапы анализа временного ряда могут включать построение графика зависимости значений от времени для проверки однородности ряда различными способами: стабильность во времени в отличие от тенденции; устойчивость локальных колебаний во времени.
Объединение информации на разных сайтах
[ редактировать ]В гидрологии анализируются ряды данных по ряду участков, состоящие из годовых значений внутригодового максимального годового стока рек. Общая модель заключается в том, что распределения этих значений одинаковы для всех объектов, за исключением простого коэффициента масштабирования, так что местоположение и масштаб связаны простым способом. Тогда могут возникнуть вопросы изучения однородности по местам распределения масштабированных значений.
Объединение источников информации
[ редактировать ]В метеорологии наборы погодных данных собираются на протяжении многих лет, и в рамках этого измерения на определенных станциях могут время от времени прекращаться, в то время как примерно в то же время измерения могут начинаться в близлежащих местах. Тогда возникают вопросы о том, можно ли считать эти записи однородными с течением времени, если записи объединяются в один более длинный набор записей. Пример проверки однородности данных о скорости и направлении ветра можно найти в Romanić et al ., 2015. [9]
Гомогенность внутри популяций
[ редактировать ]Простые опросы населения могут начинаться с идеи, что ответы будут однородными для всего населения. Оценка однородности населения предполагает изучение того, отличаются ли реакции определенных идентифицируемых субпопуляций от реакций других. Например, владельцы автомобилей могут отличаться от тех, кто не владеет автомобилем, или могут существовать различия между разными возрастными группами.
Тесты
[ редактировать ]Проверка однородности в смысле точной эквивалентности статистических распределений может быть основана на E-статистике . Тест местоположения проверяет более простую гипотезу о том, что распределения имеют одинаковый параметр местоположения .
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Греческую этимологию этого термина см. Маккалок, Дж. Хьюстон (1985). «О гетероэластичности». Эконометрика . 53 (2): 483. JSTOR 1911250 .
- ^ Уайт, Халберт (1980). «Согласованная с гетероскедастичностью ковариационная матрица оценки и прямой тест на гетероскедастичность». Эконометрика . 48 (4): 817–838. CiteSeerX 10.1.1.11.7646 . дои : 10.2307/1912934 . JSTOR 1912934 .
- ^ Гуджарати, DN; Портер, округ Колумбия (2009). Основная эконометрика (Пятое изд.). Бостон: МакГроу-Хилл Ирвин. п. 400. ИСБН 9780073375779 .
- ^ Гольдбергер, Артур С. (1964). Эконометрическая теория . Нью-Йорк: Джон Уайли и сыновья. стр. 238–243 . ISBN 9780471311010 .
- ^ Джонстон, Дж. (1972). Эконометрические методы . Нью-Йорк: МакГроу-Хилл. стр. 214–221.
- ^ Ангрист, Джошуа Д.; Пишке, Йорн-Штеффен (31 декабря 2009 г.). В основном безобидная эконометрика: спутник эмпирика . Издательство Принстонского университета. дои : 10.1515/9781400829828 . ISBN 978-1-4008-2982-8 .
- ^ Лонг, Дж. Скотт ; Триведи, Правин К. (1993). «Некоторые тесты спецификации модели линейной регрессии». В Боллене, Кеннет А.; Лонг, Дж. Скотт (ред.). Тестирование моделей структурных уравнений . Лондон: Сейдж. стр. 66–110. ISBN 978-0-8039-4506-7 .
- ^ Энгл, Роберт Ф. (июль 1982 г.). «Авторегрессионная условная гетероскедастичность с оценками дисперсии инфляции Соединенного Королевства». Эконометрика . 50 (4): 987–1007. дои : 10.2307/1912773 . ISSN 0012-9682 . JSTOR 1912773 .
- ^ Романич Д. Чурич М. Йовичич И. Ломпар М. 2015. Долгосрочные тенденции ветра Кошава в период 1949–2010 гг. Международный журнал климатологии 35(2):288-302. DOI: 10.1002/joc.3981.
Дальнейшее чтение
[ редактировать ]- Холл, М.Дж. (2003) Интерпретация неоднородных гидрометеорологических временных рядов на примере тематического исследования. Метеорологические приложения , 10, 61–67. дои : 10.1017/S1350482703005061
- Крус, DJ, и Блэкман, HS (1988). Надежность и однородность тестов с точки зрения теории порядковых тестов. Прикладные измерения в образовании, 1, 79–88 (перепечатка по запросу).
- Левинджер, Дж. (1948). Техника однородных тестов по сравнению с некоторыми аспектами масштабного анализа и факторного анализа. Психологический бюллетень, 45, 507–529.