Силовая велосиметрия Лоренца

Силовая велосиметрия Лоренца ^[1] (LFV) — это бесконтактный электромагнитный метод измерения расхода. LFV особенно подходит для измерения скорости жидких металлов, таких как сталь или алюминий , и в настоящее время разрабатывается для применения в металлургии . Измерение скорости потока в горячих и агрессивных жидкостях, таких как жидкий алюминий и расплавленное стекло, представляет собой одну из важнейших задач промышленной механики жидкостей. Помимо жидкостей, LFV также может использоваться для измерения скорости твердых материалов, а также для обнаружения микродефектов в их структурах.

Система силы Лоренца для измерения скорости называется силовым расходомером Лоренца (LFF). LFF измеряет интегральную или объемную силу Лоренца , возникающую в результате взаимодействия движущегося жидкого металла и приложенного магнитного поля. В этом случае характерная длина магнитного поля того же порядка, что и размеры канала. Следует отметить, что в случае использования локализованных магнитных полей можно выполнять измерения локальной скорости, и поэтому термин силовой велосиметр используется Лоренца.

Введение

Использование магнитных полей для измерения расхода началось в 19 веке, когда в 1832 году Майкл Фарадей попытался определить скорость реки Темзы . Фарадей применил метод, в котором поток (поток реки) подвергается воздействию магнитного поля (магнитного поля Земли), а индуцированное напряжение измеряется с помощью двух электродов, пересекающих один и тот же поток. Этот метод лежит в основе одного из наиболее успешных коммерческих применений в области измерения расхода, известного как индуктивный расходомер. Теория таких устройств была разработана и всесторонне обобщена профессором Дж. А. Шерклиффом. ^[2] в начале 1950-х годов. Хотя индуктивные расходомеры широко используются для измерения расхода жидкостей при комнатной температуре, таких как напитки, химикаты и сточные воды, они не подходят для измерения расхода таких сред, как горячие, агрессивные, а также для локальных измерений, когда окружающие препятствия ограничивают доступ к каналу или трубка. Поскольку они требуют введения электродов в жидкость, их использование ограничивается применениями при температурах, намного ниже точек плавления практически важных металлов.

Силовая скорость Лоренца была изобретена А. Шерклиффом. Однако в те первые годы он не нашел практического применения вплоть до недавних технических достижений; в производстве сильных постоянных магнитов из редкоземельных и нередкоземельных металлов, точных методов измерения силы, программного обеспечения для моделирования мультифизических процессов для решения магнитогидродинамических (МГД) задач этот принцип можно превратить в осуществимый метод измерения рабочего потока. LFV в настоящее время разрабатывается для применения в металлургии. ^[3] а также в других областях. ^[4]

На основе теории Шерклиффа было предпринято несколько попыток разработать методы измерения расхода, не требующие механического контакта с жидкостью. ^[5]^[6] Среди них — вихретоковый расходомер, который измеряет вызванные потоком изменения электрического сопротивления катушек, взаимодействующих с потоком. Совсем недавно был предложен бесконтактный метод, в котором к потоку прикладывается магнитное поле, а скорость определяется на основе измерений вызванных потоком деформаций приложенного магнитного поля. ^[7]^[8]

Принцип и физическая интерпретация

Принцип силовой велосиметрии Лоренца основан на измерении силы Лоренца , возникающей вследствие течения проводящей жидкости под действием переменного магнитного поля . Согласно закону Фарадея , когда металл или проводящая жидкость движется через магнитное поле, вихревые токи генерируются там за счет электродвижущей силы в зонах максимального градиента магнитного поля (в данном случае во входной и выходной зонах) . Вихревой ток , в свою очередь, создает индуцированное магнитное поле по закону Ампера . Взаимодействие вихревых токов с полным магнитным полем приводит к возникновению силы Лоренца, разрывающей поток. В силу третьего закона Ньютона «действие=реакция» на свой источник — постоянный магнит — действует сила той же величины, но противоположного направления. Прямое измерение силы реакции магнита позволяет определить скорость жидкости, поскольку эта сила пропорциональна скорости потока. Сила Лоренца, используемая в LFV, не имеет ничего общего с магнитным притяжением или отталкиванием. Это происходит только из-за вихревых токов, сила которых зависит от электропроводности, относительной скорости между жидкостью и постоянным магнитом, а также от величины магнитного поля.

Так, при движении жидкого металла поперек силовых линий магнитного поля взаимодействие магнитного поля (которое создается либо токоведущей катушкой, либо постоянным магнитом) с индуцированными вихревыми токами приводит к возникновению силы Лоренца (с плотностью ${\vec {f}}={\vec {j}}\times {\vec {B}}$ ), что тормозит поток. Плотность силы Лоренца примерно равна

f\sim \sigma vB^{2}

где $\sigma$ – электропроводность жидкости, $v$ его скорость и $B$ величина магнитного поля. Этот факт хорошо известен и нашел множество применений. Эта сила пропорциональна скорости и проводимости жидкости, и ее измерение является ключевой идеей LFV. С недавним появлением мощных редкоземельных постоянных магнитов (таких как NdFeB , SmCo и других видов магнитов) и инструментов для проектирования сложных систем с использованием постоянных магнитов, практическая реализация этого принципа стала возможной.

Первичное магнитное поле ${\vec {B}}\left({\vec {r}}\right)$ может быть создан постоянным магнитом или первичным током ${\vec {J}}\left({\vec {r}}\right)$ (см. рис. 1). Движение жидкости под действием первичного поля вызывает вихревые токи, которые схематически изображены на рис. 3. Их обозначим через ${\vec {j}}\left({\vec {r}}\right)$ и называются вторичными токами. Взаимодействие вторичного тока с первичным магнитным полем отвечает за силу Лоренца внутри жидкости.

{\vec {F}}_{f}=\int _{f}{\vec {j}}\times {\vec {B}}d^{3}{\vec {r}}

что нарушает поток.

Вторичные токи создают магнитное поле. ${\vec {b}}\left({\vec {r}}\right)$ , вторичное магнитное поле. Взаимодействие первичного электрического тока с вторичным магнитным полем приводит к возникновению силы Лоренца, действующей на магнитную систему.

{\vec {F}}_{m}=\int _{m}{\vec {J}}\times {\vec {b}}d^{3}{\vec {r}}

Принцип взаимности для силовой велосиметрии Лоренца гласит, что электромагнитные силы, действующие на жидкость и на магнитную систему, имеют одинаковую величину и действуют в противоположном направлении, а именно

{\vec {F}}_{m}=-{\vec {F}}_{f}

Общий закон масштабирования, который связывает измеренную силу с неизвестной скоростью, можно вывести, исходя из упрощенной ситуации, показанной на рис. 2. Здесь небольшой постоянный магнит с дипольным моментом $m$ находится на расстоянии $L$ над полубесконечной жидкостью, движущейся с равномерной скоростью $v$ параллельно его свободной поверхности.

Рис. 2: Пространственное распределение магнитных полей в силовой велосиметрии Лоренца: (а) первичное магнитное поле ${\vec {B}}$ и вихревые токи ${\vec {J}}$ создаваемый магнитным диполем, взаимодействующим с равномерно движущейся электропроводящей жидкостью; (б) вторичное магнитное поле ${\vec {b}}$ из-за горизонтальных вихревых токов ${\vec {J}}$ . Адаптировано из. ^[1]

Анализ, который приводит к масштабному соотношению, можно сделать количественным, если предположить, что магнит представляет собой точечный диполь с дипольным моментом. ${\vec {m}}=m{\hat {e}}_{z}$ магнитное поле которого определяется выражением

{\vec {B}}\left({\vec {R}}\right)={\frac {\mu _{0}}{4\pi }}\left\lbrace 3{\frac {\left({\vec {m}}\cdot {\vec {R}}\right){\vec {R}}}{R^{5}}}-{\frac {\vec {m}}{R^{3}}}\right\rbrace

где ${\vec {R}}={\vec {r}}-L{\hat {e}}_{z}$ и $R=\mid {\vec {R}}\mid$ . Предполагая поле скоростей ${\vec {v}}=v{\hat {e}}_{x}$ для $z<0$ , вихревые токи можно рассчитать по закону Ома для движущейся электропроводящей жидкости.

{\vec {J}}=\sigma \left(-\nabla \phi +{\vec {v}}\times {\vec {B}}\right)

с учетом граничных условий $J_{z}=0$ в $z=0$ и $J_{z}\to 0$ как $z\to 1$ . Во-первых, скалярный электрический потенциал получается как

\phi \left({\vec {r}}\right)=-{\frac {\mu _{0}vm}{4\pi }}{\frac {x}{R^{3}}}

из которого легко вычисляется плотность электрического тока. Они действительно горизонтальные. Как только они станут известны, закон Био-Савара можно будет использовать для расчета вторичного магнитного поля. ${\vec {b}}\left({\vec {r}}\right)$ . Наконец, сила определяется выражением

{\vec {F}}=\left({\vec {m}}\cdot \nabla \right){\vec {b}}

где градиент ${\vec {b}}$ необходимо оценивать в месте расположения диполя. Для рассматриваемой задачи все эти шаги можно выполнить аналитически без каких-либо приближений, приводящих к результату.

F={\frac {\mu _{0}^{2}\sigma vm^{2}}{128\pi L^{3}}}{\hat {e}}_{z}

Это дает нам оценку

F\sim \mu _{0}^{2}\sigma vm^{2}L^{-3}

Концептуальные установки

Силовые расходомеры Лоренца обычно подразделяют на несколько основных концептуальных конфигураций. Некоторые из них спроектированы как статические расходомеры, в которых магнитная система находится в покое и измеряется действующая на нее сила. В качестве альтернативы они могут быть сконструированы как ротационные расходомеры, в которых магниты расположены на вращающемся колесе, а скорость вращения является мерой скорости потока. Очевидно, что сила, действующая на силовой расходомер Лоренца, зависит как от распределения скорости, так и от формы магнитной системы. Эта классификация зависит от относительного направления магнитного поля, которое применяется по отношению к направлению потока. На рисунке 3 можно выделить схемы продольных и поперечных силовых расходомеров Лоренца.

Важно отметить, что даже если на рисунках изображены только катушка или магнит, принцип справедлив для обоих.

Поворотный LFF состоит из свободно вращающегося постоянного магнита. ^[9] (или набор магнитов, установленных на маховике, как показано на рисунке 4), который намагничен перпендикулярно оси, на которой он установлен. Когда такая система расположена рядом с каналом, по которому течет электропроводящий поток жидкости, она вращается так, что приводной момент, обусловленный вихревыми токами, индуцируемыми потоком, уравновешивается тормозным моментом, индуцируемым самим вращением. Равновесная скорость вращения изменяется прямо пропорционально скорости потока и обратно пропорционально расстоянию между магнитом и воздуховодом. В этом случае можно измерить либо крутящий момент магнитной системы, либо угловую скорость вращения колеса.

Рис. 4. Упрощенный эскиз роторного LFV. Адаптировано из. ^[1]

Практическое применение

Предполагается, что LFV будет распространен на все жидкие и твердые материалы при условии, что они являются электрическими проводниками. Как было показано ранее, сила Лоренца, создаваемая потоком, линейно зависит от проводимости жидкости. Обычно электропроводность расплавленных металлов составляет порядка $10^{6}~S/m$ поэтому сила Лоренца находится в пределах нескольких мН . Однако столь же важные жидкости, как расплавы стекла и электролитические растворы, имеют проводимость $\sim ~1~S/m$ порождая силу Лоренца порядка микроньютонов или даже меньше.

Высокопроводящие среды: жидкие или твердые металлы.

Среди различных возможностей измерения воздействия на магнитную систему успешно применяются те, которые основаны на измерении отклонения параллельной пружины под действием приложенной силы. ^[10] Сначала используют тензодатчик, а затем регистрируют прогиб кварцевой пружины с помощью интерферометра, при этом деформация детектируется с точностью до 0,1 нм.

Среда с низкой проводимостью: электролитический раствор или расплав стекла.

Недавний прогресс в области LFV сделал возможным измерение скорости потока сред с очень низкой электропроводностью, в частности, путем изменения параметров, а также использование некоторых современных устройств измерения силы, позволяющих измерять скорость потока растворов электролитов с проводимостью , равной 10. ⁶ раз меньше, чем для жидких металлов. Существует множество промышленных и научных применений, в которых желательно бесконтактное измерение расхода через непрозрачные стенки или непрозрачные жидкости. К таким применениям относятся измерения расхода химикатов, продуктов питания, напитков, крови, водных растворов в фармацевтической промышленности, расплавленных солей на солнечных теплоэлектростанциях, ^[11] и высокотемпературные реакторы ^[12] а также расплавы стекол для высокоточной оптики. ^[13]

Бесконтактный расходомер – это устройство, не находящееся в механическом контакте ни с жидкостью, ни со стенкой трубы, по которой течет жидкость. Бесконтактные расходомеры одинаково полезны при загрязнении стен, например, при обработке радиоактивных материалов, когда трубы сильно вибрируют или в случаях, когда необходимо разработать портативные расходомеры. Если жидкость и стенки трубы прозрачны и жидкость содержит индикаторные частицы, методы оптических измерений ^[14]^[15] являются достаточно эффективным инструментом для проведения бесконтактных измерений. Однако если стенка или жидкость непрозрачны, как это часто бывает в производстве продуктов питания, химической технологии, производстве стекла и металлургии, существует очень мало возможностей для бесконтактного измерения расхода.

Система измерения силы является важной частью силовой скорости Лоренца. Благодаря системе измерения силы с высоким разрешением возможно измерение даже более низкой проводимости. На сегодняшний день система измерения силы постоянно совершенствуется. Сначала использовались маятниковые установки (рис. 5). Одна из экспериментальных установок состоит из двух мощных (410 мТл) магнитов из NdFeB, подвешенных на тонких проволоках по обе стороны канала, тем самым создавая магнитное поле, перпендикулярное потоку жидкости, здесь отклонение измеряется системой интерферометра. ^[16]^[17] Вторая установка состоит из современной системы весового баланса (рис. 6), к которой подвешиваются оптимизированные магниты на базе матричной системы Хальбаха. Хотя общая масса обеих магнитных систем одинакова (1 кг), эта система вызывает в 3 раза больший отклик системы за счет расположения отдельных элементов в массиве и их взаимодействия с заданным профилем жидкости. Здесь желательно использовать очень чувствительные устройства для измерения силы, поскольку скорость потока преобразуется из очень маленькой обнаруженной силы Лоренца. Эта сила в сочетании с неизбежным собственным весом $F_{G}$ магнита ( $F_{G}=m\cdot g$ ) вокруг $F/F_{G}=10^{-7}$ . После этого был разработан метод измерения дифференциальных сил. В этом методе использовались два баланса: один с магнитом, другой с манекеном того же веса. Таким образом, влияние окружающей среды будет уменьшено. Недавно сообщалось, что измерения расхода этим методом возможны для потоков соленой воды, электропроводность которой составляет всего 0,06 См/м (диапазон электропроводности обычной водопроводной воды). ^[18]

Силовая сигмометрия Лоренца

Лоренц-силовая сигмометрия (LOFOS) ^[19] — бесконтактный метод измерения теплофизических свойств материалов, независимо от того, жидкость это или твердое тело. Точные измерения электрической ценности, плотности, вязкости, теплопроводности и поверхностного натяжения расплавленных металлов имеют большое значение в промышленности. Одной из основных проблем экспериментальных измерений теплофизических свойств при высоких температурах (>1000 К) в жидком состоянии является проблема химической реакции между горячей жидкостью и электрическими зондами.Основное уравнение для расчета электропроводности выводится из уравнения, связывающего массовый расход ${\dot {m}}$ и сила Лоренца $F$ создаваемое магнитным полем в потоке:

{\dot {m}}\left(t\right)={\frac {K}{\Sigma }}F\left(t\right)\quad

где $\Sigma ={\frac {\sigma }{\rho }}$ - удельная электропроводность равна отношению электропроводности $\sigma$ и массовая плотность жидкости $\rho$ . $K$ — это калибровочный коэффициент, который зависит от геометрии системы LOFOS.

Из уравнения выше совокупная масса во время работы определяется как

M=\int _{t1}^{t2}{\dot {m}}\left(t\right)dt={\frac {K}{\Sigma }}\int _{t1}^{t2}F\left(t\right)dt={\frac {K}{\Sigma }}{\tilde {F}}\quad ,

где ${\tilde {F}}$ – интеграл силы Лоренца во временном процессе. Из этого уравнения и учитывая конкретную формулу электропроводности можно вывести окончательное уравнение для расчета электропроводности жидкости в форме

\sigma =\rho K{\frac {\tilde {F}}{M}}\quad .

Времяпролетная силовая велосиметрия Лоренца

Рис. 9: Принцип работы времяпролетного режима. Взято из ^[20]

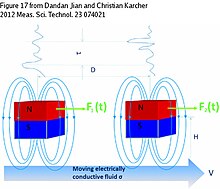
Времяпролетная силовая велосиметрия Лоренца, ^[20]^[21] предназначен для бесконтактного определения скорости потока в проводящих жидкостях. Его можно успешно использовать даже в том случае, когда такие свойства материала, как электропроводность или плотность, точно не известны в конкретных внешних условиях. Последняя причина делает времяпролетные LFV особенно важными для промышленного применения. По времяпролетному ЛФВ (рис. 9) на канале поочередно монтируются две когерентные измерительные системы. Измерение основано на получении кросс-корреляционной функции сигналов, регистрируемых двумя магнитными измерительными системами. Каждая система состоит из постоянного магнита и датчика силы, поэтому наведение силы Лоренца и измерение силы реакции производятся одновременно. Любая функция взаимной корреляции полезна только в случае качественного различия между сигналами и для создания различия в этом случае используются турбулентные колебания. Перед достижением зоны измерения канала жидкость проходит искусственный вихревой генератор, вызывающий в нем сильные возмущения. И когда такой пульсационный вихрь достигает магнитного поля измерительной системы, мы можем наблюдать пик на его силово-временной характеристике, в то время как вторая система все еще измеряет стабильный поток. Тогда по времени между пиками и расстоянию между измерительными системами наблюдатель может оценить среднюю скорость и, следовательно, расход жидкости по уравнению:

Q_{flow}=k{\frac {D}{\tau }}

где $D$ расстояние между магнитной системой, $\tau$ временная задержка между зарегистрированными пиками и $k$ получается экспериментально для каждой конкретной жидкости, как показано на рисунке 9.

Вихретоковые испытания силой Лоренца

Рис. 10: Принцип работы LET. Адаптировано из ^[22]

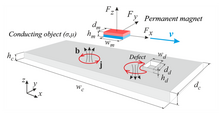
Другой, хотя и физически тесно связанной, задачей является обнаружение глубоко залегающих дефектов и неоднородностей в электропроводящих твердых материалах.

В традиционной версии вихретокового контроля переменное (переменное) магнитное поле используется для индуцирования вихревых токов внутри исследуемого материала. Если в материале имеется трещина или дефект, которые делают пространственное распределение электропроводности неоднородным, путь вихревых токов нарушается и импеданс катушки, генерирующей переменное магнитное поле, изменяется. Таким образом, измеряя импеданс этой катушки, можно обнаружить трещину. Поскольку вихревые токи генерируются переменным магнитным полем, их проникновение в приповерхностную область материала ограничивается скин-эффектом . Поэтому применимость традиционной версии вихретокового контроля ограничивается анализом непосредственной близости от поверхности материала, обычно порядка одного миллиметра. Попытки преодолеть это фундаментальное ограничение с помощью низкочастотных катушек и сверхпроводящих датчиков магнитного поля не привели к широкому применению.

Недавний метод, называемый вихретоковым испытанием силой Лоренца (LET), ^[22]^[23] использует преимущества применения магнитных полей постоянного тока и относительного движения, обеспечивая глубокие и относительно быстрые испытания электропроводящих материалов. В принципе, LET представляет собой модификацию традиционного вихретокового контроля, от которого он отличается в двух аспектах, а именно (i) как индуцируются вихревые токи и (ii) как обнаруживается их возмущение. В ЛЭТ вихревые токи генерируются путем обеспечения относительного движения между испытуемым проводником и постоянным магнитом (см. рисунок 10). Если магнит проходит мимо дефекта, действующая на него сила Лоренца вызывает искажение, обнаружение которого является ключом к принципу работы ЛПЭ. Если объект не имеет дефектов, результирующая сила Лоренца остается постоянной.

Преимущества и ограничения

Преимущества LFV:

LFV – это бесконтактный метод измерения расхода.
LFV может успешно применяться для агрессивных и высокотемпературных жидкостей, таких как жидкие металлы.
Средний расход или среднюю скорость жидкости можно получить независимо от неоднородностей потока и зон турбулентности.

Ограничения LFV:

Необходимость температурного контроля измерительной системы из-за сильной зависимости магнитного поля магнита от температуры. Высокая температура может привести к безвозвратной потере магнитных свойств постоянного магнита (температура Кюри).
Ограничение зоны измерения размерами постоянного магнита.
Необходимость контроля уровня жидкости при работе с открытым каналом.
Быстрое затухание магнитных полей приводит к возникновению крошечных сил, действующих на магнитную систему.

См. также

Внешние ссылки

Официальная веб-страница группы Лоренц-силовой скорости и группы испытаний вихретоковых токов Лоренца.

Ссылки

^ Jump up to: ^а ^б ^с Тесс, А.; Вотяков Е.В.; Колесников Ю. (25 апреля 2006 г.). «Лоренц-силовая скорость» . Письма о физических отзывах . 96 (16). Американское физическое общество (APS): 164601. doi : 10.1103/physrevlett.96.164501 . ISSN 0031-9007 . ПМИД 16712237 .
^ Артур Дж. Шерклифф: Теория измерения электромагнитного потока . Издательство Кембриджского университета, ISBN 978-0-521-33554-6 .
^ Колесников Юрий; Керхер, Кристиан; Тесс, Андре (24 февраля 2011 г.). «Силовой расходомер Лоренца для жидкого алюминия: лабораторные эксперименты и заводские испытания» . Металлургические операции и операции с материалами B . 42 (3). Springer Science and Business Media LLC: 441–450. дои : 10.1007/s11663-011-9477-6 . ISSN 1073-5615 .
^ Jump up to: ^а ^б «Научно-учебная группа ЛОРЕНТЦ ФОРС» . Архивировано из оригинала 17 ноября 2013 г. Проверено 9 апреля 2012 г.
^ Приеде, Янис; Бушенау, Доминик; Гербет, Гюнтер (8 апреля 2011 г.). «Бесконтактный электромагнитный фазовращательный расходомер для жидких металлов». Измерительная наука и технология . 22 (5): 055402. arXiv : 1010.0404 . дои : 10.1088/0957-0233/22/5/055402 . ISSN 0957-0233 . S2CID 118416619 .
^ Jump up to: ^а ^б Тесс, Андре; Вотяков, Евгений; Кнепен, Бернард; Зиканов, Олег (31 августа 2007 г.). «Теория силового расходомера Лоренца» . Новый журнал физики . 9 (8). Издательство IOP: 299. doi : 10.1088/1367-2630/9/8/299 . hdl : 2027.42/58171 . ISSN 1367-2630 .
^ Баумгартль, Дж.; Юбер, А.; Мюллер, Г. (1993). «Использование магнитогидродинамических эффектов для исследования течения жидкости в электропроводящих расплавах». Физика жидкостей A: Гидродинамика . 5 (12). Издательство AIP: 3280–3289. дои : 10.1063/1.858685 . ISSN 0899-8213 .
^ Стефани, Фрэнк; Гандрам, Томас; Гербет, Гюнтер (16 ноября 2004 г.). «Бесконтактная индуктивная проточная томография». Физический обзор E . 70 (5): 056306. arXiv : физика/0409036 . дои : 10.1103/physreve.70.056306 . ISSN 1539-3755 . ПМИД 15600752 . S2CID 16047774 .
^ Приеде, Янис; Бушенау, Доминик; Гербет, Гюнтер (2011). «Одномагнитный ротационный расходомер для жидких металлов». Журнал прикладной физики . 110 (3): 034512. arXiv : 1012.3965 . дои : 10.1063/1.3610440 . ISSN 0021-8979 . S2CID 119270549 .
^ Хейнике, Кристиана; Тымпель, Саския; Пулугундла, Гаутама; Ранеберг, Илько; Бек, Томас; Тесс, Андре (15 декабря 2012 г.). «Взаимодействие небольшого постоянного магнита с потоком жидкого металла в канале» . Журнал прикладной физики . 112 (12). Издательство AIP: 124914. doi : 10.1063/1.4770155 . ISSN 0021-8979 .
^ Херрманн, Ульф; Келли, Брюс; Прайс, Генри (2004). «Двухрезервуарное хранилище расплавленной соли для солнечных электростанций с параболическим желобом». Энергия . 29 (5–6). Эльзевир Б.В.: 883–893. дои : 10.1016/s0360-5442(03)00193-2 . ISSN 0360-5442 .
^ Форсберг, Чарльз В.; Петерсон, Пер Ф.; Пикард, Пол С. (2003). «Усовершенствованный высокотемпературный реактор с расплавленным солевым охлаждением для производства водорода и электроэнергии» . Ядерные технологии . 144 (3). Информа UK Limited: 289–302. дои : 10.13182/nt03-1 . ISSN 0029-5450 .
^ У. Ланге и Х. Лох, «Нестабильность и стабилизация потока в стеклянных трубах» в «Математическом моделировании в технологии стекла» , серия Шотта по стеклу и стеклокерамике, под редакцией Д. Краузе и Х. Лоха (Springer Verlag, 2002).
^ К. Тропеа, А. Л. Ярин и Дж. Фосс, Справочник по экспериментальной механике жидкости, Springer-Verlag, GmbH, 2007 г.
^ Ф. Дерст, А. Меллинг и Дж. Х. Уайтлоу, Принципы и практика лазерной допплеровской анемометрии , 2-е изд. Академический, Лондон, 1981 г.
^ Вегфрасс, Андре; Дитхольд, Кристиан; Вернер, Майкл; Резак, Кристиан; Фрелих, Томас; Хальбедель, Бернд; Тесс, Андре (24 августа 2012 г.). «Измерение расхода слабопроводящих жидкостей с использованием силовой скорости Лоренца». Измерительная наука и технология . 23 (10). Издание IOP: 105307. doi : 10.1088/0957-0233/23/10/105307 . ISSN 0957-0233 . S2CID 62792251 .
^ Jump up to: ^а ^б Дитхольд, Кристиан; Хилбруннер, Фалько (11 июня 2012 г.). «Измерение малых сил в сочетании с высокими собственными нагрузками с использованием компенсации электромагнитной силы». Измерительная наука и технология . 23 (7). Издание IOP: 074017. doi : 10.1088/0957-0233/23/7/074017 . ISSN 0957-0233 . S2CID 120932577 .
^ Васильян, Сурен (2015). «К измерению водопроводной воды с помощью силы Лоренца» . Измерительная наука и технология . 26 (11): 115302. Бибкод : 2015MeScT..26k5302V . дои : 10.1088/0957-0233/26/11/115302 . S2CID 124006180 .
^ Улиг, Роберт П.; Зец, Младен; Циолковский, Марек; Брауэр, Хартмут; Тесс, Андре (2012). «Лоренц-силовая сигмометрия: бесконтактный метод измерения электропроводности» . Журнал прикладной физики . 111 (9). Издательство AIP: 094914. doi : 10.1063/1.4716005 . ISSN 0021-8979 .
^ Jump up to: ^а ^б Цзян, Дандан; Керхер, Кристиан (11 июня 2012 г.). «Измерения электромагнитного потока в жидких металлах с использованием времяпролетной силовой скорости Лоренца». Измерительная наука и технология . 23 (7). Издание IOP: 074021. doi : 10.1088/0957-0233/23/7/074021 . ISSN 0957-0233 . S2CID 59032287 .
^ Вире, Аксель; Кнепен, Бернард; Тесс, Андре (2010). «Силовая скорость Лоренца на основе измерений времени пролета». Физика жидкостей . 22 (12). Издательство AIP: 125101. doi : 10.1063/1.3517294 . ISSN 1070-6631 .
^ Jump up to: ^а ^б М. Зец и др., Быстрая методика расчета силы Лоренца в приложениях неразрушающего контроля, COMPUMAG 2013, Будапешт, Венгрия
^ Улиг, Роберт П.; Зец, Младен; Брауэр, Хартмут; Тесс, Андре (24 июля 2012 г.). «Испытание вихревых токов силой Лоренца: модель прототипа». Журнал неразрушающего контроля . 31 (4). ООО «Спрингер Сайенс энд Бизнес Медиа»: 357–372. дои : 10.1007/s10921-012-0147-7 . ISSN 0195-9298 . S2CID 73628551 .

[ThessPRL-1] Jump up to: ^а ^б ^с Тесс, А.; Вотяков Е.В.; Колесников Ю. (25 апреля 2006 г.). «Лоренц-силовая скорость» . Письма о физических отзывах . 96 (16). Американское физическое общество (APS): 164601. doi : 10.1103/physrevlett.96.164501 . ISSN 0031-9007 . ПМИД 16712237 .

[Shercliff-2] Артур Дж. Шерклифф: Теория измерения электромагнитного потока . Издательство Кембриджского университета, ISBN 978-0-521-33554-6 .

[Kolesnikov2011-3] Колесников Юрий; Керхер, Кристиан; Тесс, Андре (24 февраля 2011 г.). «Силовой расходомер Лоренца для жидкого алюминия: лабораторные эксперименты и заводские испытания» . Металлургические операции и операции с материалами B . 42 (3). Springer Science and Business Media LLC: 441–450. дои : 10.1007/s11663-011-9477-6 . ISSN 1073-5615 .

[TUI-4] Jump up to: ^а ^б «Научно-учебная группа ЛОРЕНТЦ ФОРС» . Архивировано из оригинала 17 ноября 2013 г. Проверено 9 апреля 2012 г.

[Priede2011-5] Приеде, Янис; Бушенау, Доминик; Гербет, Гюнтер (8 апреля 2011 г.). «Бесконтактный электромагнитный фазовращательный расходомер для жидких металлов». Измерительная наука и технология . 22 (5): 055402. arXiv : 1010.0404 . дои : 10.1088/0957-0233/22/5/055402 . ISSN 0957-0233 . S2CID 118416619 .

[Thess2007-6] Jump up to: ^а ^б Тесс, Андре; Вотяков, Евгений; Кнепен, Бернард; Зиканов, Олег (31 августа 2007 г.). «Теория силового расходомера Лоренца» . Новый журнал физики . 9 (8). Издательство IOP: 299. doi : 10.1088/1367-2630/9/8/299 . hdl : 2027.42/58171 . ISSN 1367-2630 .

[Baumgartl1993-7] Баумгартль, Дж.; Юбер, А.; Мюллер, Г. (1993). «Использование магнитогидродинамических эффектов для исследования течения жидкости в электропроводящих расплавах». Физика жидкостей A: Гидродинамика . 5 (12). Издательство AIP: 3280–3289. дои : 10.1063/1.858685 . ISSN 0899-8213 .

[Stefani2004-8] Стефани, Фрэнк; Гандрам, Томас; Гербет, Гюнтер (16 ноября 2004 г.). «Бесконтактная индуктивная проточная томография». Физический обзор E . 70 (5): 056306. arXiv : физика/0409036 . дои : 10.1103/physreve.70.056306 . ISSN 1539-3755 . ПМИД 15600752 . S2CID 16047774 .

[Priede2010-9] Приеде, Янис; Бушенау, Доминик; Гербет, Гюнтер (2011). «Одномагнитный ротационный расходомер для жидких металлов». Журнал прикладной физики . 110 (3): 034512. arXiv : 1012.3965 . дои : 10.1063/1.3610440 . ISSN 0021-8979 . S2CID 119270549 .

[Heinecke2012-10] Хейнике, Кристиана; Тымпель, Саския; Пулугундла, Гаутама; Ранеберг, Илько; Бек, Томас; Тесс, Андре (15 декабря 2012 г.). «Взаимодействие небольшого постоянного магнита с потоком жидкого металла в канале» . Журнал прикладной физики . 112 (12). Издательство AIP: 124914. doi : 10.1063/1.4770155 . ISSN 0021-8979 .

[Herrmann-11] Херрманн, Ульф; Келли, Брюс; Прайс, Генри (2004). «Двухрезервуарное хранилище расплавленной соли для солнечных электростанций с параболическим желобом». Энергия . 29 (5–6). Эльзевир Б.В.: 883–893. дои : 10.1016/s0360-5442(03)00193-2 . ISSN 0360-5442 .

[Forsberg-12] Форсберг, Чарльз В.; Петерсон, Пер Ф.; Пикард, Пол С. (2003). «Усовершенствованный высокотемпературный реактор с расплавленным солевым охлаждением для производства водорода и электроэнергии» . Ядерные технологии . 144 (3). Информа UK Limited: 289–302. дои : 10.13182/nt03-1 . ISSN 0029-5450 .

[LangeandLoch-13] У. Ланге и Х. Лох, «Нестабильность и стабилизация потока в стеклянных трубах» в «Математическом моделировании в технологии стекла» , серия Шотта по стеклу и стеклокерамике, под редакцией Д. Краузе и Х. Лоха (Springer Verlag, 2002).

[Tropea-14] К. Тропеа, А. Л. Ярин и Дж. Фосс, Справочник по экспериментальной механике жидкости, Springer-Verlag, GmbH, 2007 г.

[Durst-15] Ф. Дерст, А. Меллинг и Дж. Х. Уайтлоу, Принципы и практика лазерной допплеровской анемометрии , 2-е изд. Академический, Лондон, 1981 г.

[Wegfrass2-16] Вегфрасс, Андре; Дитхольд, Кристиан; Вернер, Майкл; Резак, Кристиан; Фрелих, Томас; Хальбедель, Бернд; Тесс, Андре (24 августа 2012 г.). «Измерение расхода слабопроводящих жидкостей с использованием силовой скорости Лоренца». Измерительная наука и технология . 23 (10). Издание IOP: 105307. doi : 10.1088/0957-0233/23/10/105307 . ISSN 0957-0233 . S2CID 62792251 .

[Diethold_2012-17] Jump up to: ^а ^б Дитхольд, Кристиан; Хилбруннер, Фалько (11 июня 2012 г.). «Измерение малых сил в сочетании с высокими собственными нагрузками с использованием компенсации электромагнитной силы». Измерительная наука и технология . 23 (7). Издание IOP: 074017. doi : 10.1088/0957-0233/23/7/074017 . ISSN 0957-0233 . S2CID 120932577 .

[Vasilyan1-18] Васильян, Сурен (2015). «К измерению водопроводной воды с помощью силы Лоренца» . Измерительная наука и технология . 26 (11): 115302. Бибкод : 2015MeScT..26k5302V . дои : 10.1088/0957-0233/26/11/115302 . S2CID 124006180 .

[Uhlig2012-19] Улиг, Роберт П.; Зец, Младен; Циолковский, Марек; Брауэр, Хартмут; Тесс, Андре (2012). «Лоренц-силовая сигмометрия: бесконтактный метод измерения электропроводности» . Журнал прикладной физики . 111 (9). Издательство AIP: 094914. doi : 10.1063/1.4716005 . ISSN 0021-8979 .

[Jian2012-20] Jump up to: ^а ^б Цзян, Дандан; Керхер, Кристиан (11 июня 2012 г.). «Измерения электромагнитного потока в жидких металлах с использованием времяпролетной силовой скорости Лоренца». Измерительная наука и технология . 23 (7). Издание IOP: 074021. doi : 10.1088/0957-0233/23/7/074021 . ISSN 0957-0233 . S2CID 59032287 .

[Vire2010-21] Вире, Аксель; Кнепен, Бернард; Тесс, Андре (2010). «Силовая скорость Лоренца на основе измерений времени пролета». Физика жидкостей . 22 (12). Издательство AIP: 125101. doi : 10.1063/1.3517294 . ISSN 1070-6631 .

[Zec2013-22] Jump up to: ^а ^б М. Зец и др., Быстрая методика расчета силы Лоренца в приложениях неразрушающего контроля, COMPUMAG 2013, Будапешт, Венгрия

[Uhlig2013-23] Улиг, Роберт П.; Зец, Младен; Брауэр, Хартмут; Тесс, Андре (24 июля 2012 г.). «Испытание вихревых токов силой Лоренца: модель прототипа». Журнал неразрушающего контроля . 31 (4). ООО «Спрингер Сайенс энд Бизнес Медиа»: 357–372. дои : 10.1007/s10921-012-0147-7 . ISSN 0195-9298 . S2CID 73628551 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]