Универсальная вершина

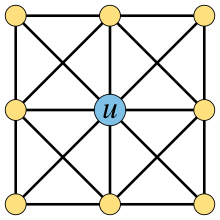
В теории графов универсальная вершина — это вершина , неориентированного графа смежная со всеми остальными вершинами графа. Ее также можно назвать доминирующей вершиной , поскольку она образует одноэлементное доминирующее множество в графе. Граф, содержащий универсальную вершину, можно назвать конусом , а его универсальную вершину — вершиной конуса. ^[1] Эту терминологию следует отличать от несвязанного использования этих слов для кванторов универсальности в логике графов и для вершинных графов .

Графы, содержащие универсальную вершину, включают звезды , тривиально совершенные графы и графы дружбы . Для колесных графов (графов пирамид ) и графов пирамидальных многогранников более высокой размерности вершина вершины пирамиды является универсальной. Когда граф содержит универсальную вершину, это граф «коп-выигрыш» , и почти все графы «коп-выигрыш» содержат универсальную вершину.

Количество помеченных графов, содержащих универсальную вершину, можно подсчитать методом включения-исключения , показывая, что на любом четном количестве вершин существует нечетное количество таких графов. Это, в свою очередь, можно использовать, чтобы показать, что свойство наличия универсального графа является уклончивым : проверка этого свойства может потребовать проверки смежности всех пар вершин. Однако универсальную вершину можно узнать сразу по ее степени : в $n$ -вершинный граф, он имеет степень $n-1$ . Универсальные вершины можно описать короткой логической формулой, которая использовалась в алгоритмах графов для определения связанных свойств.

В специальных семействах графов

Звезды — это именно те деревья , которые имеют универсальную вершину и могут быть построены путем добавления универсальной вершины к независимому множеству . Колесообразные графы аналогичным образом могут быть сформированы путем добавления универсальной вершины к циклическому графу . ^[2] ( Тривиально совершенные графы графы сравнимости теоретико -порядковых деревьев ) всегда содержат универсальную вершину, корень дерева, и, более строго, их можно охарактеризовать как графы, в которых каждый связный индуцированный подграф содержит универсальную вершину. ^[3]Связные пороговые графы образуют подкласс тривиально совершенных графов, поэтому они также содержат универсальную вершину; их можно определить как графы, которые можно сформировать путем многократного добавления либо универсальной вершины, либо изолированной вершины (без инцидентных ребер). ^[4]

В геометрии трехмерные пирамиды имеют в качестве скелетов колесные графы . ^[5] и, в более общем смысле, пирамида более высокой размерности - это многогранник, грани которого всех измерений соединяют вершину со всеми гранями основания более низкой размерности, включая все вершины основания. Говорят, что многогранник имеет пирамидальную форму в вершине и может иметь более одной вершины. Однако существование соседних многогранников означает, что граф многогранника может иметь универсальную вершину или все вершины универсальны, при этом сам многогранник не является пирамидой. ^[6]

Теорема дружбы Пола Эрдеша , Альфреда Реньи и Веры Т. Сос ( 1966 ) утверждает, что если каждые две вершины в конечном графе имеют ровно одного общего соседа, то граф содержит универсальную вершину. Графы, описываемые этой теоремой, представляют собой графы дружбы , образованные системами треугольников, соединенных вместе в общей общей вершине, универсальной вершине. ^[7] Предположение о конечности графа важно; существуют бесконечные графы, в которых каждые две вершины имеют одного общего соседа, но не имеют универсальной вершины. ^[8]

Каждый граф с универсальной вершиной является разборным графом , то есть его можно свести к одной вершине путем многократного удаления вершин, чьи замкнутые окрестности являются подмножествами замкнутых окрестностей других вершин. Любая последовательность удаления, которая оставляет универсальную вершину на месте и удаляет все остальные вершины, соответствует этому определению. Почти все разборные графы имеют универсальную вершину в том смысле, что доля $n$ -вершинные разбираемые графы, у которых универсальная вершина в пределе стремится к единице как $n$ уходит в бесконечность. Разбираемые графы также называются графами победы полицейского, поскольку сторона, играющая в полицейского, выигрывает в определенной игре «полицейский и грабитель», определенной на этих графах. ^[9]

Когда граф имеет универсальную вершину, набор вершин, состоящий только из этой вершины, является доминирующим набором , набором, который включает в себя каждую вершину или является смежным с каждой вершиной. По этой причине в контексте задач о доминирующем множестве универсальную вершину можно также назвать доминирующей вершиной . ^[10] Для сильного произведения графов $G\boxtimes H$ , числа доминирования $\gamma (G)$ и $\gamma (H)$ подчиняться неравенствам $\max\{\gamma (G),\gamma (H)\}\leq \gamma (G\boxtimes H)\leq \gamma (G)\gamma (H).$ Это означает, что сильное произведение имеет доминирующую вершину тогда и только тогда, когда она есть у обоих его сомножителей; в этом случае верхняя граница его доминирующего числа равна единице, а в любом другом случае нижняя граница больше единицы. ^[11]

Комбинаторное перечисление

Количество размеченных графов с $n$ вершины, по крайней мере одна из которых является универсальной (или, что эквивалентно, изолированной в дополнительном графе ), могут быть подсчитаны по принципу включения-исключения , в котором подсчитываются графы, в которых одна выбранная вершина является универсальной, а затем исправляется превышение подсчета путем вычитания вершины. подсчеты для графов с двумя выбранными универсальными вершинами, затем сложение счетчиков для графов с тремя выбранными универсальными вершинами и т. д. В результате получается формула

\displaystyle \sum _{k=1}^{n}(-1)^{k+1}{\binom {n}{k}}2^{\tbinom {n-k}{2}}.

В каждом члене суммы $k$ - количество вершин, выбранных универсальными, и ${\tbinom {n}{k}}$ - количество способов сделать этот выбор. ${\tbinom {n-k}{2}}$ - это количество пар вершин, которые не включают выбранную универсальную вершину, и, принимая это число за показатель степени двойки, подсчитывает количество графов с выбранными вершинами как универсальные. ^[12]

Начиная с $n=1$ , это количество графов:

1, 1, 4, 23, 256, 5319, 209868, 15912975, 2343052576, 675360194287, ... (последовательность A327367 в OEIS ). ^[13]

Для $n>1$ , эти числа являются нечетными, когда $n$ четно, и наоборот. ^[12] Неразмеченная версия этой задачи перечисления графов тривиальна в том смысле, что число $n$ -вершинные непомеченные графы с универсальной вершиной равны числу $(n-1)$ -вершинные графы. ^[13]

Признание

На графике с $n$ вершин, универсальная вершина — это вершина, степень которой равна точно $n-1$ . ^[10]

Свойство наличия универсальной вершины можно выразить формулой логики графов первого порядка . С использованием $\sim$ для обозначения отношения смежности в графе, граф $G$ имеет универсальную вершину тогда и только тогда, когда она моделирует формулу $\exists u\forall v{\bigl (}(u\neq v)\Rightarrow (u\sim v){\bigr )}.$ Существование этой формулы и ее небольшое количество чередований между универсальными и экзистенциальными кванторами можно использовать в управляемом алгоритме с фиксированным параметром для проверки того, можно ли сделать так, чтобы все компоненты графа имели универсальные вершины с помощью $k$ шаги удаления вершины из каждого компонента. ^[14]

Свойство наличия универсальной вершины (или, что то же самое, изолированной вершины) рассматривалось в связи с гипотезой Андераа-Карпа-Розенберга о том, сколько запросов (вызовов подпрограмм) необходимо, чтобы проверить, обладает ли помеченный граф свойством при наличии доступа к граф только с помощью подпрограммы, которая может проверить, являются ли две заданные вершины смежными. На графике с $n$ вершин, можно определить весь граф и проверить любое свойство, используя ${\tbinom {n}{2}}$ запросы. Свойство графа является уклончивым , если ни один алгоритм не может проверить это свойство, гарантируя меньшее количество запросов. Проверка существования универсальной вершины на графах с четным числом вершин невозможна. Существует нечетное количество таких графов, имеющих универсальную вершину. Алгоритм тестирования может быть вынужден запросить все пары вершин с помощью подпрограммы смежности, которая всегда отвечает таким образом, чтобы оставить нечетное количество оставшихся графов, имеющих универсальную вершину. Пока все ребра не проверены, общее количество оставшихся графов будет четным, поэтому алгоритм не сможет определить, имеет ли запрашиваемый граф универсальную вершину. ^[12]

Ссылки

^ Ларрион, Ф.; де Мелло, CP; Моргана, А.; Нойманн-Лара, В .; Писанья, Массачусетс (2004), «Оператор клики на кографах и серийных графах», Discrete Mathematics , 282 (1–3): 183–191, doi : 10.1016/j.disc.2003.10.023 , MR 2059518 .
^ Бонато, Энтони (2008), Курс веб-графа , Аспирантура по математике, том. 89, Атлантическая ассоциация исследований в области математических наук (AARMS), Галифакс, Северная Каролина, стр. 89. 7, номер домена : 10.1090/gsm/089 , ISBN 978-0-8218-4467-0 , МР 2389013 .
^ Волк, Э.С. (1962), «Граф сравнимости дерева», Proceedings of the American Mathematical Society , 13 (5): 789–795, doi : 10.2307/2034179 , JSTOR 2034179 , MR 0172273 .
^ Хватал, Вацлав ; Хаммер, Питер Ладислав (1977), «Агрегация неравенств в целочисленном программировании», в Хаммере, Польша; Джонсон, Эл.; Корте, БХ; Немхаузер, Г.Л. (ред.), Исследования по целочисленному программированию (Proc. Worksh. Bonn, 1975) , Annals of Discrete Mathematics, vol. 1, Амстердам: Северная Голландия, стр. 145–162 .
^ Писански, Томаж ; Серватиус, Бриджит (2013), Конфигурация с графической точки зрения , Springer, стр. 21, номер домена : 10.1007/978-0-8176-8364-1 , ISBN 978-0-8176-8363-4
^ Клее, Виктор (1964), «О количестве вершин выпуклого многогранника», Canadian Journal of Mathematics , 16 : 701–720, doi : 10.4153/CJM-1964-067-6 , MR 0166682
^ Эрдос, Пол ; Реньи, Альфред ; Сос, Вера Т. (1966), «Об одной задаче теории графов» (PDF) , Studia Sci. Венгерский. , 1 : 215–235 .
^ Хватал, Вацлав ; Коциг, Антон ; Розенберг, Иво Г.; Дэвис, Рой О. (1976), «Есть $\scriptstyle 2^{\aleph _{\alpha }}$ Графики дружбы кардинала $\scriptstyle \aleph _{\alpha }$ ", Canadian Mathematical Bulletin , 19 (4): 431–433, doi : 10.4153/cmb-1976-064-1 .
^ Бонато, Энтони; Кемкес, Грэм; Пралат, Павел (2012), «Почти все графы выигрыша копов содержат универсальную вершину», Discrete Mathematics , 312 (10): 1652–1657, doi : 10.1016/j.disc.2012.02.018 , MR 2901161 .
^ Jump up to: ^а ^б Хейнс, Тереза В .; Хедетниеми, Стивен Т .; Хеннинг, Майкл А. (2023), Доминирование в графах: основные понятия , Монографии Спрингера по математике, Спрингер, Чам, стр. 2, номер домена : 10.1007/978-3-031-09496-5 , ISBN 978-3-031-09495-8 , МР 4607811
^ Фишер, Дэвид К. (1994), «Доминирование, дробное доминирование, 2-упаковка и графовые произведения», SIAM Journal on Discrete Mathematics , 7 (3): 493–498, doi : 10.1137/S0895480191217806 , MR 1285586
^ Jump up to: ^а ^б ^с Ловас, Ласло ; Янг, Нил Э. (2002), «Конспекты лекций об уклончивости свойств графов», arXiv : cs/0205031
^ Jump up to: ^а ^б Слоан, Нью-Джерси (редактор), «Последовательность A327367 (количество помеченных простых графов с n вершинами, по крайней мере одна из которых изолирована)» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS
^ Фомин Федор Владимирович ; Головач Петр А.; Тиликос, Димитриос М. (2021), «Параметризованная сложность расстояния исключения до логических свойств первого порядка», 36-й ежегодный симпозиум ACM/IEEE по логике в информатике, LICS 2021, Рим, Италия, 29 июня – 2 июля 2021 г. , IEEE, стр. 1–13, arXiv : 2104.02998 , doi : 10.1109/LICS52264.2021.9470540 , ISBN. 978-1-6654-4895-6 , S2CID 233169117

[1] Ларрион, Ф.; де Мелло, CP; Моргана, А.; Нойманн-Лара, В .; Писанья, Массачусетс (2004), «Оператор клики на кографах и серийных графах», Discrete Mathematics , 282 (1–3): 183–191, doi : 10.1016/j.disc.2003.10.023 , MR 2059518 .

[2] Бонато, Энтони (2008), Курс веб-графа , Аспирантура по математике, том. 89, Атлантическая ассоциация исследований в области математических наук (AARMS), Галифакс, Северная Каролина, стр. 89. 7, номер домена : 10.1090/gsm/089 , ISBN 978-0-8218-4467-0 , МР 2389013 .

[3] Волк, Э.С. (1962), «Граф сравнимости дерева», Proceedings of the American Mathematical Society , 13 (5): 789–795, doi : 10.2307/2034179 , JSTOR 2034179 , MR 0172273 .

[4] Хватал, Вацлав ; Хаммер, Питер Ладислав (1977), «Агрегация неравенств в целочисленном программировании», в Хаммере, Польша; Джонсон, Эл.; Корте, БХ; Немхаузер, Г.Л. (ред.), Исследования по целочисленному программированию (Proc. Worksh. Bonn, 1975) , Annals of Discrete Mathematics, vol. 1, Амстердам: Северная Голландия, стр. 145–162 .

[5] Писански, Томаж ; Серватиус, Бриджит (2013), Конфигурация с графической точки зрения , Springer, стр. 21, номер домена : 10.1007/978-0-8176-8364-1 , ISBN 978-0-8176-8363-4

[6] Клее, Виктор (1964), «О количестве вершин выпуклого многогранника», Canadian Journal of Mathematics , 16 : 701–720, doi : 10.4153/CJM-1964-067-6 , MR 0166682

[7] Эрдос, Пол ; Реньи, Альфред ; Сос, Вера Т. (1966), «Об одной задаче теории графов» (PDF) , Studia Sci. Венгерский. , 1 : 215–235 .

[8] Хватал, Вацлав ; Коциг, Антон ; Розенберг, Иво Г.; Дэвис, Рой О. (1976), «Есть $\scriptstyle 2^{\aleph _{\alpha }}$ Графики дружбы кардинала $\scriptstyle \aleph _{\alpha }$ ", Canadian Mathematical Bulletin , 19 (4): 431–433, doi : 10.4153/cmb-1976-064-1 .

[9] Бонато, Энтони; Кемкес, Грэм; Пралат, Павел (2012), «Почти все графы выигрыша копов содержат универсальную вершину», Discrete Mathematics , 312 (10): 1652–1657, doi : 10.1016/j.disc.2012.02.018 , MR 2901161 .

[h3-10] Jump up to: ^а ^б Хейнс, Тереза В .; Хедетниеми, Стивен Т .; Хеннинг, Майкл А. (2023), Доминирование в графах: основные понятия , Монографии Спрингера по математике, Спрингер, Чам, стр. 2, номер домена : 10.1007/978-3-031-09496-5 , ISBN 978-3-031-09495-8 , МР 4607811

[11] Фишер, Дэвид К. (1994), «Доминирование, дробное доминирование, 2-упаковка и графовые произведения», SIAM Journal on Discrete Mathematics , 7 (3): 493–498, doi : 10.1137/S0895480191217806 , MR 1285586

[evasiveness-12] Jump up to: ^а ^б ^с Ловас, Ласло ; Янг, Нил Э. (2002), «Конспекты лекций об уклончивости свойств графов», arXiv : cs/0205031

[oeis-13] Jump up to: ^а ^б Слоан, Нью-Джерси (редактор), «Последовательность A327367 (количество помеченных простых графов с n вершинами, по крайней мере одна из которых изолирована)» , Интернет -энциклопедия целочисленных последовательностей , Фонд OEIS

[14] Фомин Федор Владимирович ; Головач Петр А.; Тиликос, Димитриос М. (2021), «Параметризованная сложность расстояния исключения до логических свойств первого порядка», 36-й ежегодный симпозиум ACM/IEEE по логике в информатике, LICS 2021, Рим, Италия, 29 июня – 2 июля 2021 г. , IEEE, стр. 1–13, arXiv : 2104.02998 , doi : 10.1109/LICS52264.2021.9470540 , ISBN. 978-1-6654-4895-6 , S2CID 233169117

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]