График знакомств
| График знакомств | |
|---|---|
 | |
| Вершины | 112 |
| Края | 336 |
| Радиус | 7 |
| Диаметр | 7 |
| Обхват | 4 |
| Автоморфизмы | 2688 |
| Таблица графиков и параметров | |
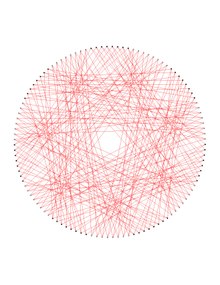
В математической области теории графов граф Дейтера представляет собой 6-регулярный граф со 112 вершинами и 336 ребрами. [1] [2] [3] [4] [5] [6] [7] Граф Дейтераполученное удалением копиикода Хэмминга длины 7 из двоичного кода7- куб .
Граф Дейтера и, как следствие, любой граф, полученный удалением кода Хэмминга длины 2. р -1 от а(2 р -1) -куб , является симметричным графом .В частности, граф Дейтера допускает 3- факторизацию на двакопии люблянского графа , который является третьим наименьшим из существующих полусимметричных кубических графов регулярной степени 3. Люблянский граф имеет обхват 10.
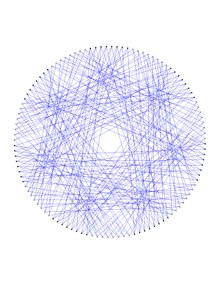
Фактически доказано, что граф Дейтера может быть двухцветным, скажем, в цветовом наборе {красный, синий}, как на верхнем рисунке справа, так что как результирующие монохроматические по краям красные, так и синие вершины подграфы являются копиями люблянского графа . Эти две копии содержат ровно 112 вершин графа Дейтера и по 168 ребер каждая, причем обе копии имеют обхват 10, тогда как граф Дейтера имеет обхват 6 и 7-кубический обхват 4. Кажется, что граф Дейтера является наименьшим симметричным графом, имеющим связный самодополнительный полусимметричный кубический подграф, охватывающий вершины.
И красный, и синий люблянские подграфы, охватывающие вершины графа Дейтера, могут быть представлены как покрывающие графы графа Хивуда , а именно как 8-покрытия графа Хивуда . Это предлагается в каждом из двух представлений графа Любляны (красный вверху, синий внизу, оба справа) путём поочередного окрашивания прообразов последовательных вершин графа Хивуда , скажем, в чёрный и белый цвета (лучше рассмотреть с помощью дважды щелкнув по изображению для увеличения рисунка), в соответствии с графа Хивуда двуразделением . Каждое такое обратное изображение формируется 8 соседями вдоль фиксированного координатного направления 7-куба половины кода Хэмминга, имеющего фиксированный вес 0 или 1. Путем обмена этими весами посредством перестановки (0 1), можно перейти от смежности, предлагаемой красным графом Любляны, к смежности, предлагаемой синим графом Любляны, или наоборот.
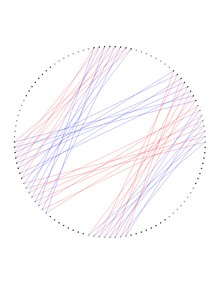
Одна седьмая часть графика Дейтера представлена на отдельном рисунке ниже, который можно получить из двух полученных копий графика Хивуда .
Ссылки
[ редактировать ]- ^ Клин М.; Лаури Дж.; Зив-Ав М. «Связи между двумя полусимметричными графами на 112вершины через призму ассоциативных схем», Жур. СимволическоеКомпьютер., 47–10, 2012, 1175–1191.
- ^ Борхес Дж.; Дейтер И.Я. «О совершенных доминирующих множествах вгиперкубы и их дополнения», J. Combin. Math. Combin. Comput.20 (1996), 161–173
- ^ Дейтер И.Я. "О симметричных подграфах7-куба: обзор», Discrete Math. 124 (1994) 55–66.
- ^ Дейтер И.Дж. "Симметрия факторов 7-куба Хэмминга"оболочка», J. Combin. Des. 5 (1997), 301–309.
- ^ Дейтер И.Дж.;Гуань П. «Подмножества ребер, блокирующих квадрат в гиперкубах и вершинах».избегание», теория графов, комбинаторика, алгоритмы изаявки (Сан-Франциско, Калифорния, 1989 г.), 162–174, SIAM, Филадельфия,Пенсильвания, 1991 г.
- ^ Дейтер И.Дж.; Пужоль Ж. «Совершенное доминирование и симметрия в гиперкубах», Труды двадцать шестой конференции.Юго-восточная международная конференция по комбинаторике, теории графови вычислительная техника (Бока-Ратон, Флорида, 1995 г.). Конгресс Число. 111 (1995),18–32
- ^ Дейтер И.Дж.; Weichsel PM "Twisted Perfect"доминирующие подграфы гиперкубов», ТрудыДвадцать четвертая Юго-Восточная международная конференция поКомбинаторика, теория графов и вычисления (Бока-Ратон, Флорида, 1993).Конгресс Число. 94 (1993), 67–78