Граф покрытия

В математической дисциплине теории графов граф графом , $C$ является покрывающим другой граф $G$ если существует карта покрытия из вершин множества $C$ в множество вершин $G.$ , Накрывающая карта $f$ является сюръекцией и локальным изоморфизмом : окрестность вершины $v$ в $C$ отображается биективно в окрестность ⁠ $f(v)$ ⁠ в $Г.$

Термин «лифт» часто используется как синоним покрывающего графа связного графа .

Хотя это может ввести в заблуждение, не существует (очевидной) связи между графом покрытия и покрытием вершин или покрытием ребер .

Комбинаторная формулировка покрывающих графов непосредственно обобщается на случай мультиграфов . Покрывающий граф является частным случаем покрывающего комплекса. ^[1] Как накрывающие комплексы, так и мультиграфы с одномерным клеточным комплексом являются не чем иным, как примерами накрытия топологических пространств , поэтому терминология теории накрытия пространств имеется; скажем, накрывающая группа преобразований, универсальное накрытие, абелевое накрытие и максимальное абелевое накрытие. ^[2]

Определение

Пусть G = ( V ₁ , E ₁ ) и C = ( V ₂ , E ₂ ) — два графа, и пусть f : V ₂ → V ₁ — сюръекция . Тогда f является покрывающим отображением из C в G каждого v ∈ V ₂ ограничение f на окрестность v , является биекцией на окрестность f ( v ) в G. если для Иначе говоря, f отображает ребра, инцидентные v, взаимно однозначно на ребра, инцидентные f ( v ).

существует покрывающее отображение из C в G , то C является графом или лифтом G. покрывающим Если h -лифт — это такой лифт, что накрывающее отображение f обладает тем свойством, что для каждой вершины v графа G ее слой f ⁻¹(v) содержит ровно h элементов.

Примеры

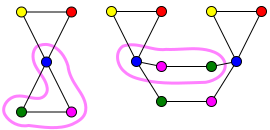
На следующем рисунке граф C является графом, покрывающим граф H .

карта покрытия f от C до H. Цветом обозначена Например, обе синие вершины C отображаются в синюю H. вершину Карта f является сюръекцией: каждая вершина H имеет прообраз в C . Более того, f окрестность вершины v в C на окрестность вершины f ( v ) в H. взаимно однозначно отображает каждую

Например, пусть v — одна из фиолетовых вершин в C ; у него есть два соседа в C : зеленая вершина u и синяя вершина t . Аналогично, пусть v ′ будет фиолетовой вершиной в H ; у него есть два соседа в H : зеленая вершина u ′ и синяя вершина t ′ . Отображение f, ограниченное { t , u , v } , является биекцией на { t ′ , u ′ , v ′ }. Это показано на следующем рисунке:

Аналогично мы можем проверить, что окрестность синей вершины в C взаимно однозначно отображается в окрестность синей вершины в H :

Двойная крышка

В приведенном выше примере каждая вершина H прообраза в C. имеет ровно два Следовательно, — двукратное или двойное накрытие H C .

Для любого графа G можно построить двудольное двойное покрытие G , которое является двудольным графом покрытием G. и двойным Двудольное двойное покрытие G — это тензорное произведение графов G × K ₂ :

Если G уже двудольная, то ее двудольное двойное накрытие состоит из двух непересекающихся G. копий Граф может иметь множество различных двойных покрытий, кроме двудольного двойного покрытия.

Универсальная крышка

Для любого связного графа G можно построить его универсальный граф покрытия . ^[3] Это пример более общей концепции универсального покрытия из топологии; топологическое требование, чтобы универсальное покрытие было односвязным, в терминах теории графов переводится в требование, чтобы оно было ацикличным и связным; то есть дерево .Универсальный накрывающий граф единственен (с точностью до изоморфизма). Если G — дерево, то G сам по себе является универсальным графом покрытия G . Для любого другого конечного связного графа G универсальный накрывающий граф G является счетным (но локально конечным) деревом.

Универсальный граф покрытия T связного графа G можно построить следующим образом. Выберите произвольную вершину r группы G в качестве отправной точки. Каждая вершина T представляет собой обход без возврата, который начинается с r , то есть последовательность w = ( r , v ₁ , v ₂ , ..., v _n ) вершин G такая, что

vi _для и vi _{+1 w} смежны в G всех i , т. е. — прогулка
v _{i -1} ≠ v _{i +1} для всех i , т. е. w не имеет возврата.

Тогда две вершины T смежны, если одна является простым расширением другой: вершина ( r , v ₁ , v ₂ , ..., v _n ) смежна с вершиной ( r , v ₁ , v ₂ , . .., v _{n -1} ). С точностью до изоморфизма одно и то же дерево T строится независимо от выбора начальной точки r .

Накрывающая карта f отображает вершину ( r ) в T в вершину r в G и вершину ( r , v ₁ , v ₂ , ..., v _n ) в T в вершину v _n в G .

Примеры универсальных чехлов

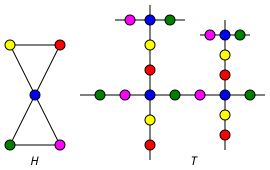
Следующий рисунок иллюстрирует универсальный граф покрытия T графа H ; цвета обозначают карту покрытия.

Для любого k все k - регулярные графы имеют одно и то же универсальное покрытие: бесконечное k -регулярное дерево.

Топологический кристалл

Бесконечно кратный абелев граф, покрывающий конечный (мульти)граф, называется топологическим кристаллом, абстракцией кристаллических структур. Например, кристалл алмаза как граф является максимальным абелевым графом покрытия четырехреберного дипольного графа . Эта точка зрения в сочетании с идеей «стандартных реализаций» оказывается полезной при систематическом проектировании (гипотетических) кристаллов. ^[2]

Плоское покрытие

Плоское покрытие графа — это конечный покрывающий граф, который сам является плоским графом . Свойство иметь плоское покрытие можно охарактеризовать запретными минорами , но точная характеристика этой формы остается неизвестной. Каждый граф с вложением в проективную плоскость имеет плоское накрытие, исходящее из ориентируемого двойного накрытия проективной плоскости; в 1988 году Сейя Нагами предположил, что это единственные графы с плоскими покрытиями, но это осталось недоказанным. ^[4]

Графики напряжения

Распространенный способ формирования покрывающих графов использует графы напряжения , в которых дротики данного графа G (то есть пары направленных ребер, соответствующие неориентированным ребрам G ) помечены обратными парами элементов из некоторой группы . Производный граф графика напряжения имеет в качестве вершин пары ( v , x ), где v — вершина G , а x — элемент группы; дротик от v до w, помеченный элементом группы y в G, соответствует ребру от ( v , x ) до ( w , xy ) в производном графе.

Таким образом, универсальное покрытие можно рассматривать как производный граф графа напряжения, в котором ребра остовного дерева графа помечены единичным элементом группы, а каждая оставшаяся пара дротиков помечена отдельным порождающим элементом. элемент свободной группы . Таким образом, двудольный дубль можно рассматривать как производный график графика напряжения, в котором каждый дротик помечен ненулевым элементом группы второго порядка.

Примечания

^ Ротман, Джозеф (декабрь 1973 г.). «Покрытие комплексов приложениями к алгебре». Математический журнал Роки Маунтин . 3 (4): 641–674. дои : 10.1216/RMJ-1973-3-4-641 .
^ Перейти обратно: ^а ^б Сунада, Тошиказу (2012). «6 топологических кристаллов». Топологическая кристаллография: взгляд на дискретный геометрический анализ . Спрингер. стр. 73–90. ISBN 978-4-431-54177-6 .
^ Англия 1980
^ Хлинены, Петр (2010). «20 лет гипотезы Негами о плоском покрытии» (PDF) . Графы и комбинаторика . 26 (4): 525–536. CiteSeerX 10.1.1.605.4932 . дои : 10.1007/s00373-010-0934-9 . МР 2669457 . .

Ссылки

Годсил, Крис ; Ройл, Гордон Ф. (2001). «§6.8 Складни и обложки» . Алгебраическая теория графов . Тексты для аспирантов по математике. Том. 207. Спрингер. стр. 114–6. ISBN 978-0-387-95220-8 .
Амит, Алон; Линиал, Натан ; Матушек, Иржи ; Розенман, Эяль (2001). «Случайные подъемы графиков» . Материалы двенадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA '01) . Общество промышленной и прикладной математики. стр. 883–894. CiteSeerX 10.1.1.719.3508 . ISBN 978-0-89871-490-6 .
Англуин, Дана (1980). «Локальные и глобальные свойства в сетях процессоров (Расширенное резюме)». Материалы двенадцатого ежегодного симпозиума ACM по теории вычислений (STOC '80) . Ассоциация вычислительной техники. стр. 82–93. дои : 10.1145/800141.804655 . ISBN 978-0-89791-017-0 .

[1] Ротман, Джозеф (декабрь 1973 г.). «Покрытие комплексов приложениями к алгебре». Математический журнал Роки Маунтин . 3 (4): 641–674. дои : 10.1216/RMJ-1973-3-4-641 .

[sunada-2] Перейти обратно: ^а ^б Сунада, Тошиказу (2012). «6 топологических кристаллов». Топологическая кристаллография: взгляд на дискретный геометрический анализ . Спрингер. стр. 73–90. ISBN 978-4-431-54177-6 .

[3] Англия 1980

[4] Хлинены, Петр (2010). «20 лет гипотезы Негами о плоском покрытии» (PDF) . Графы и комбинаторика . 26 (4): 525–536. CiteSeerX 10.1.1.605.4932 . дои : 10.1007/s00373-010-0934-9 . МР 2669457 . .

[1]

[2]

[3]

[4]