Парадокс Хупера

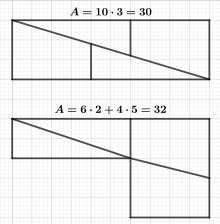
Парадокс Хупера

Парадокс Хупера — это ложный парадокс, основанный на оптической иллюзии. Геометрическую фигуру площадью 32 единицы разбивают на четыре части, которые затем собираются в прямоугольник площадью всего 30 единиц.

Объяснение

Объяснение парадокса Хупера. Коричневый параллелограмм — это область перекрытия двух треугольников.

При внимательном рассмотрении можно заметить, что треугольники рассеченной формы не идентичны треугольникам прямоугольника. Длина меньшей стороны под прямым углом в исходной форме составляет 2 единицы, а в прямоугольнике — только 1,8 единицы. Это означает, что настоящие треугольники исходной формы перекрываются в прямоугольнике. Область перекрытия представляет собой параллелограмм, диагонали и стороны которого можно вычислить с помощью теоремы Пифагора .

$d_{1}={\sqrt {2^{2}+1^{2}}}={\sqrt {5}}$

$d_{2}={\sqrt {3^{2}+10^{2}}}={\sqrt {109}}$

$s_{1}={\sqrt {2^{2}+6^{2}}}={\sqrt {40}}$

$s_{2}={\sqrt {1^{2}+4^{2}}}={\sqrt {17}}$

Площадь этого параллелограмма можно определить по формуле Герона для треугольников. Это дает

$s={\frac {d_{1}+s_{1}+s_{2}}{2}}={\frac {{\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}}}{2}}$

для половины окружности треугольника (половины параллелограмма) и с тем же для площади параллелограмма

${\begin{aligned}F&=2\cdot {\sqrt {s\cdot (s-s_{1})\cdot (s-s_{2})\cdot (s-d_{1})}}\\[5pt]&=2\cdot {\frac {1}{4}}\cdot {\sqrt {({\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}})\cdot (-{\sqrt {5}}+{\sqrt {17}}+{\sqrt {40}})\cdot ({\sqrt {5}}-{\sqrt {17}}+{\sqrt {40}})\cdot ({\sqrt {5}}+{\sqrt {17}}-{\sqrt {40}})}}\\[5pt]&=2\cdot {\frac {1}{4}}\cdot {\sqrt {16}}\\[5pt]&=2\end{aligned}}$.

Таким образом, площадь перекрытия двух треугольников точно соответствует исчезнувшей площади в 2 единицы.

История

Уильям Хупер опубликовал парадокс в 1774 году в своей книге «Рациональные развлечения» , назвав его «Геометрическими деньгами». Издание его книги 1774 года все еще содержало ложный рисунок, который был исправлен в издании 1782 года. Однако Хупер не был первым, кто опубликовал эту геометрическую ошибку, поскольку книга Хупера была в значительной степени адаптацией книги Эдме-Жиля Гийо « Новые воссоздания физики и математики» , которая была опубликована во Франции в 1769 году. Описание в этой книге содержит ту же ложную информацию. рисунок как в книге Хупера, но он был исправлен и в более позднем издании.

См. также

• Парадокс шахматной доски
• Недостающий квадратный пазл

Ссылки

• Мартин Гарднер : Математика, магия и тайна . Курьер (Дувр), 1956 г. ISBN   9780486203355 , С. 129–155.
• Грег Н. Фредериксон: Рассечение: плоскость и фантазия . Издательство Кембриджского университета, 2003 г., ISBN   9780521525824 , глава 23, стр. 268–277, в частности стр. 271–274 ( онлайн-обновление главы 23 )
• Саймон Во время: Современные чары: культурная сила светской магии . Издательство Гарвардского университета, 2004 г., ISBN   978-0674013711 , с. 87
• Уильям Хупер: Рациональные развлечения . Лондон, 1774 г., стр. 286–287 (ошибочное 1-е издание)
• Уильям Хупер: Рациональные развлечения . Лондон, 1782 г., стр. 286–287 (исправленное 2-е издание).

Внешние ссылки

• Парадокс Хупера: как это возможно? на сайте Cut-the-knot.org
• Мариано Томатис: Проклятие хрустальных черепов и другие головоломки с исчезающей областью
• Рациональные развлечения У. Хупера