Парадокс шахматной доски

Парадокс шахматной доски

доски Парадокс шахматной или парадокс Лойда и Шлёмильха представляет собой ложный парадокс, основанный на оптической иллюзии. Шахматная доска или квадрат со стороной 8 единиц разрезана на четыре части. Эти четыре части используются для формирования прямоугольника с длиной стороны 13 и 5 единиц. Следовательно, общая площадь всех четырех частей составляет 64 единицы площади в квадрате и 65 единиц площади в прямоугольнике. Это кажущееся противоречие возникает из-за оптической иллюзии, поскольку четыре части не помещаются точно в прямоугольник, а оставляют небольшую едва видимую область. разрыв вокруг диагонали прямоугольника. Этот парадокс иногда приписывают американскому изобретателю головоломок Сэму Лойду (1841–1911) и немецкому математику Оскару Шлёмильху (1832–1901).

Анализ

Увеличенный точный рисунок показывает разрыв в прямоугольнике в форме параллелограмма.

При внимательном рассмотрении можно увидеть, что четыре части не совсем подходят друг к другу, а оставляют небольшой, едва видимый зазор по диагонали прямоугольника. Этот разрыв $DEBF$ имеет форму параллелограмма, в чем можно убедиться, показав, что противолежащие углы равны.

${\begin{aligned}\angle FDE&=90^{\circ }-\angle FDG-\angle EDI\\[6pt]&=90^{\circ }-\arctan \left({\frac {|EI|}{|DI|}}\right)-\arctan \left({\frac {|FG|}{|DG|}}\right)\\[6pt]&=90^{\circ }-\arctan \left({\frac {5}{2}}\right)-\arctan \left({\frac {3}{8}}\right)\\[6pt]&=90^{\circ }-\arctan \left({\frac {|FJ|}{|BJ|}}\right)-\arctan \left({\frac {|EH|}{|BH|}}\right)\\[6pt]&=90^{\circ }-\angle FBJ-\angle EBH\\[6pt]&=\angle FBE\approx 1.24536^{\circ }\end{aligned}}$

${\begin{aligned}\angle DEB&=360^{\circ }-\angle DEI-\angle IEH-\angle EBH\\[6pt]&=360^{\circ }-\arctan \left({\frac {|DI|}{|EI|}}\right)-90^{\circ }-\arctan \left({\frac {|DG|}{|FG|}}\right)\\[6pt]&=360^{\circ }-\arctan \left({\frac {2}{5}}\right)-90^{\circ }-\arctan \left({\frac {8}{3}}\right)\\[6pt]&=360^{\circ }-\arctan \left({\frac {|BJ|}{|FJ|}}\right)-90^{\circ }-\arctan \left({\frac {|BH|}{|EH|}}\right)\\[6pt]&=360^{\circ }-\angle BFJ-\angle JFG-\angle GFD\\[6pt]&=\angle DFB\approx 178.75464^{\circ }\end{aligned}}$

Точное расположение четырех частей вдоль прямоугольника требует, чтобы параллелограмм схлопнулся в сегменты прямой, а это означает, что он должен иметь следующие размеры:

$\angle FBE=\angle FDE=0^{\circ }$

$\angle DFB=\angle DEB=180^{\circ }$

Поскольку фактические углы лишь незначительно отклоняются от этих значений, это создает оптическую иллюзию, что параллелограмм представляет собой всего лишь отрезок прямой, а части точно совпадают. В качестве альтернативы можно проверить параллельность, поместив реактивный угол в систему координат и сравнив наклоны или векторное представление сторон.

Длина стороны и диагонали параллелограмма равны:

$|DE|=|FB|={\sqrt {2^{2}+5^{2}}}={\sqrt {29}}$

$|DF|=|EB|={\sqrt {3^{2}+8^{2}}}={\sqrt {73}}$

$|EF|={\sqrt {1^{2}+3^{2}}}={\sqrt {10}}$

$|DB|={\sqrt {5^{2}+13^{2}}}={\sqrt {194}}$

Используя формулу Герона, можно вычислить площадь половины параллелограмма ( $\triangle DFG$). Половинная окружность равна

$s={\frac {|EF|+|DE|+|DF|}{2}}={\frac {{\sqrt {10}}+{\sqrt {29}}+{\sqrt {73}}}{2}}$

что дает площадь всего параллелограмма:

${\begin{aligned}F&=2\cdot {\sqrt {s\cdot (s-|EF|)\cdot (s-|DE|)\cdot (s-|DF|)}}\\[5pt]&=2\cdot {\frac {1}{4}}\cdot {\sqrt {({\sqrt {10}}+{\sqrt {29}}+{\sqrt {73}})\cdot (-{\sqrt {10}}+{\sqrt {29}}+{\sqrt {73}})\cdot ({\sqrt {10}}-{\sqrt {29}}+{\sqrt {73}})\cdot ({\sqrt {10}}+{\sqrt {29}}-{\sqrt {73}})}}\\[5pt]&=2\cdot {\frac {1}{4}}\cdot 2\\[5pt]&=1\end{aligned}}$

Таким образом, площадь зазора составляет ровно дополнительную площадь прямоугольника.

Обобщение

Обобщенное рассечение квадрата с использованием чисел Фибоначчи.

: ${\frac {f_{n-2}}{f_{n}}}\approx {\frac {f_{n-3}}{f_{n-1}}}\Rightarrow \tan(\alpha )\approx \tan(\beta )\Rightarrow \alpha \approx \beta$,
Треугольники $T_{1},T_{2},T_{3},T_{4}$ почти похожи.

Диссекция без несовпадения площадей $\varphi ={\frac {1+{\sqrt {5}}}{2}}$

Сегменты линий, встречающиеся на рисунках последних глав, имеют длину 2, 3, 5, 8 и 13. Все это последовательные числа Фибоначчи, что предполагает обобщение схемы разреза, основанной на числах Фибоначчи. Свойства чисел Фибоначчи также позволяют глубже понять, почему оптическая иллюзия работает так хорошо. Квадрат, длина стороны которого равна числу Фибоначчи. $f_{n}$ можно разрезать, используя отрезки длины $f_{n},f_{n-1},f_{n-2}$ таким же образом шахматная доска была разрезана отрезками длиной 8, 5, 3 (см. рисунок).

Личность Кассини гласит:

$f_{n+1}\cdot f_{n-1}-f_{n}^{2}=(-1)^{n}$

Отсюда сразу становится ясно, что разница в площади между квадратом и прямоугольником всегда должна составлять 1 единицу площади, в частности, для исходного парадокса шахматной доски:

$13\cdot 5-8^{2}=f_{7}\cdot f_{5}-f_{6}^{2}=(-1)^{6}=1$

Обратите внимание, что для неравномерного индекса $n$ площадь квадрата не меньше на одну единицу площади, а больше. В этом случае четыре части не создают небольшого зазора при сборке в прямоугольник, а вместо этого слегка перекрываются. Поскольку разница в площади всегда составляет 1 единицу площади, оптическую иллюзию можно улучшить, используя большие числа Фибоначчи, позволяя проценту зазора в площади прямоугольника стать сколь угодно малым и, следовательно, для практических целей невидимым.

Поскольку отношение соседних чисел Фибоначчи довольно быстро сходится к золотому сечению $\varphi$, следующие соотношения также быстро сходятся:

${\frac {f_{n}}{f_{n-2}}}={\frac {f_{n}}{f_{n-1}}}\cdot {\frac {f_{n-1}}{f_{n-2}}}\rightarrow \varphi ^{2},\,{\frac {f_{n-2}}{f_{n}}}={\frac {f_{n-2}}{f_{n-1}}}\cdot {\frac {f_{n-1}}{f_{n}}}\rightarrow \varphi ^{-2}$

Чтобы четыре выреза квадрата точно совпали и образовали прямоугольник, используйте небольшой параллелограмм. $DEBF$ необходимо свернуть в отрезок, являющийся диагональю прямоугольника. В этом случае для углов в прямоугольнике справедливо следующее, поскольку они являются соответствующими углами параллелей:

$\angle IDE=\angle HEB$, $\angle DEI=\angle EBH$, $\angle FDG=\angle BFJ$, $\angle GFD=\angle JBF$

В результате следующие прямоугольные треугольники $\triangle IED$, $\triangle HBE$ , $\triangle DFG$ и $\triangle FBJ$ должны быть одинаковыми и соотношение их ног должно быть одинаковым.

Благодаря указанной выше быстрой сходимости соответствующие соотношения чисел Фибоначчи в собранном прямоугольнике практически одинаковы:

${\frac {f_{n}}{f_{n-2}}}\approx {\frac {f_{n-1}}{f_{n-3}}},\,{\frac {f_{n-2}}{f_{n}}}\approx {\frac {f_{n-3}}{f_{n-1}}}$

Следовательно, они почти точно подходят друг к другу, что создает оптическую иллюзию.

Можно также посмотреть на углы параллелограмма, как в исходном анализе шахматной доски. Для этих углов можно вывести следующие формулы:

$n\geq 4:\quad \angle FBE=\angle FDE=\arctan \left({\frac {1}{f_{2n-3}+2f_{n-3}f_{n-2}}}\right)\rightarrow 0^{\circ }$

$n\geq 4:\quad \angle DFB=\angle DEB=180^{\circ }-\arctan \left({\frac {1}{f_{2n-3}+2f_{n-3}f_{n-2}}}\right)\rightarrow 180^{\circ }$

Следовательно, углы быстро сходятся к значениям, необходимым для точного соответствия.

Однако можно использовать схему разреза, не создавая несоответствия площадей, то есть четыре выреза соберутся точно в прямоугольник той же площади, что и квадрат. Вместо использования чисел Фибоначчи анализ основывается непосредственно на самом золотом сечении (см. рисунок). Для квадрата с длиной стороны $a$ это дает площадь прямоугольника

$(\varphi -1)a\cdot (\varphi a)=(\varphi ^{2}-\varphi )a^{2}=a^{2},$

с $\varphi ^{2}-\varphi =1$ является свойством золотого сечения.

История

Парадокс Хупера

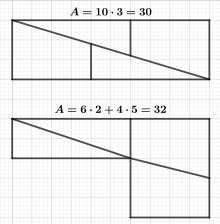
Парадокс Хупера можно рассматривать как предшественник шахматного парадокса. В нем у вас есть та же самая фигура из четырех частей, собранная в прямоугольник, однако расчлененная форма, из которой происходят эти четыре части, еще не является квадратом, а задействованные отрезки линий не основаны на числах Фибоначчи. Хупер опубликовал парадокс, ныне названный в его честь, под названием «Геометрические деньги» в своей книге «Рациональные развлечения» . Однако это не было его изобретением, поскольку его книга, по сути, представляла собой перевод книги «Новые развлечения по физике и математике» Эдме Жиля Гийо (1706–1786), опубликованной во Франции в 1769 году».

Первая известная публикация настоящего шахматного парадокса принадлежит немецкому математику Оскару Шлёмильху. Он опубликовал его в 1868 году под названием Ein geometrisches Paradoxon («геометрический парадокс») в немецком научном журнале Zeitschrift für Mathematik und Physik . В том же журнале Виктор Шлегель опубликовал в 1879 году статью Verallgemeinerung eines geometrischen Paradoxons («обобщение геометрического парадокса»), в которой обобщил конструкцию и указал на связь с числами Фибоначчи. Парадокс шахматной доски был также любимым британским математиком и писателем Льюисом Кэрроллом , который также работал над обобщением, но не опубликовал его. Позже это было обнаружено в его записях после его смерти. Американский изобретатель головоломок Сэм Лойд утверждал, что представил парадокс шахматной доски на Всемирном шахматном конгрессе в 1858 году, а позже он был включен в «Циклопедию 5000 головоломок, трюков и головоломок» Сэма Лойда (1914), которая была посмертно опубликована его сыном того же автора. имя. Сын заявил, что собрать из четырех частей фигуру из 63 единиц площади (см. рисунок вверху) было его идеей. Однако оно было опубликовано уже в 1901 году в статье Несколько открыточных головоломок Уолтера Декстера.

См. также

• Недостающий квадратный пазл

Дальнейшее чтение

• Жан-Поль Делаэ: Au платит за парадоксы . Гуменсис, 2014, ISBN   9782842451363 (французский)
• Миодраг Петкович: Знаменитые загадки великих математиков . АМС, 2009, ISBN   9780821848142 , стр. 14, 30–31.
• А. Ф. Горадам: «Последовательности Фибоначчи и геометрический парадокс». В: Журнал «Математика» , вып. 35, нет. 1 (январь 1962 г.), стр. 1–11 ( JSTOR )
• Дэвид Сингмастер: «Загадки с исчезающими областями» . В: Журнал «Рекреационная математика» , вып. 1 марта 2014 г.
• Джон Ф. Лэмб-младший: «Загадка о разрезании ковров». В: Учитель математики , Band 80, Nr. 1 (январь 1987 г.), стр. 12–14 ( JSTOR )
• Уоррен Уивер: «Льюис Кэрролл и геометрический парадокс». В: The American Mathematical Monthly , vol. 45, нет. 4 (апрель 1938 г.), стр. 234–236 ( JSTOR )
• Оскар Шлёмильх : «Геометрический парадокс». В: Журнал математики и физики , вып. 13, 1868, с. 162 (немецкий)
• Виктор Шлегель : «Обобщение геометрического парадокса». В: Журнал математики и физики , вып. 24, 1879 г., стр. 123–128 (немецкий язык).

Внешние ссылки

• Пазл-парадокс
• Вайсштейн, Эрик В. «Заблуждение о расчленении» . Математический мир .