Внутриклассовая корреляция

Точечный график, показывающий набор данных с высокой внутриклассовой корреляцией. Ценности из одной и той же группы, как правило, схожи.

Точечный график, показывающий набор данных с низкой внутриклассовой корреляцией. Тенденция к сходству ценностей одной и той же группы очень незначительна.

В статистике — внутриклассовая корреляция , или коэффициент внутриклассовой корреляции ( ICC ), — это описательная статистика , которую можно использовать при проведении количественных измерений на единицах, организованных в группы. Он описывает, насколько сильно единицы в одной группе похожи друг на друга. Хотя он рассматривается как тип корреляции , в отличие от большинства других показателей корреляции, он работает с данными, структурированными как группы, а не с данными, структурированными как парные наблюдения.

Внутриклассовая корреляция обычно используется для количественной оценки степени, в которой люди с фиксированной степенью родства (например, полные братья и сестры) похожи друг на друга с точки зрения количественного признака (см. Наследственность ). Еще одним известным применением является оценка последовательности или воспроизводимости количественных измерений, выполненных разными наблюдателями, измеряющими одну и ту же величину.

Раннее определение ICC: беспристрастная, но сложная формула

Самая ранняя работа по внутриклассовым корреляциям была сосредоточена на случае парных измерений, и первой предложенной статистикой внутриклассовой корреляции (ICC) были модификации межклассовой корреляции (корреляция Пирсона).

Рассмотрим набор данных, состоящий из N парных значений данных ( x _{n ,1} , x _{n ,2} ) для n = 1, ..., N . внутриклассовая корреляция r Первоначально предложенная Фишер Рональд является

$r={\frac {1}{Ns^{2}}}\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}}),$

где

${\bar {x}}={\frac {1}{2N}}\sum _{n=1}^{N}(x_{n,1}+x_{n,2}),$

$s^{2}={\frac {1}{2N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}\right\}.$

Более поздние версии этой статистики использовали степени свободы 2 N −1 в знаменателе для расчета s ² и N −1 в знаменателе для вычисления r , так что s ² становится несмещенным, а r становится несмещенным, если s известно .

Ключевое различие между этой ICC и межклассовой корреляцией (Пирсона) заключается в том, что данные объединяются для оценки среднего значения и дисперсии. Причина этого в том, что в ситуации, когда желательна внутриклассовая корреляция, пары считаются неупорядоченными. Например, если мы изучаем сходство близнецов, обычно не существует значимого способа упорядочить значения для двух людей в паре близнецов. Как и межклассовая корреляция, внутриклассовая корреляция для парных данных будет ограничена интервалом [ -1, +1].

Внутриклассовая корреляция также определяется для наборов данных с группами, имеющими более двух значений. Для групп, состоящих из трех значений, он определяется как

$r={\frac {1}{3Ns^{2}}}\sum _{n=1}^{N}\left\{(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}})+(x_{n,1}-{\bar {x}})(x_{n,3}-{\bar {x}})+(x_{n,2}-{\bar {x}})(x_{n,3}-{\bar {x}})\right\},$

где

${\bar {x}}={\frac {1}{3N}}\sum _{n=1}^{N}(x_{n,1}+x_{n,2}+x_{n,3}),$

$s^{2}={\frac {1}{3N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,3}-{\bar {x}})^{2}\right\}.$

По мере роста количества элементов в группе растет и количество членов перекрестного произведения в этом выражении. Проще вычислить следующую эквивалентную форму:

$r={\frac {K}{K-1}}\cdot {\frac {N^{-1}\sum _{n=1}^{N}({\bar {x}}_{n}-{\bar {x}})^{2}}{s^{2}}}-{\frac {1}{K-1}},$

где K — количество значений данных на группу, а ${\bar {x}}_{n}$ — выборочное среднее n ^й группа. Эту форму обычно приписывают Харрису . Левый член неотрицательен; следовательно, внутриклассовая корреляция должна удовлетворять

$r\geq {\frac {-1}{K-1}}.$

Для больших K этот ICC почти равен

${\frac {N^{-1}\sum _{n=1}^{N}({\bar {x}}_{n}-{\bar {x}})^{2}}{s^{2}}},$

которую можно интерпретировать как долю общей дисперсии, обусловленную различиями между группами. Рональд Фишер посвятил целую главу внутриклассовой корреляции в своей классической книге «Статистические методы для научных работников» .

Для данных из совокупности, которая полностью зашумлена, формула Фишера дает значения ICC, которые распределены около 0, т.е. иногда являются отрицательными. Это связано с тем, что Фишер разработал формулу как несмещенную, и поэтому ее оценки иногда завышаются, а иногда занижаются. Для небольших или нулевых базовых значений в генеральной совокупности ICC, рассчитанный на основе выборки, может быть отрицательным.

Современные определения ICC: более простая формула, но положительная предвзятость

Начиная с Рональда Фишера, внутриклассовая корреляция рассматривалась в рамках дисперсионного анализа (ANOVA), а в последнее время – в рамках моделей случайных эффектов . Был предложен ряд оценок ICC. Большинство оценок можно определить в терминах модели случайных эффектов.

$Y_{ij}=\mu +\alpha _{j}+\varepsilon _{ij},$

где Y _ij - это i ^й наблюдение в j ^й группа, μ — ненаблюдаемое общее среднее значение , α _j — ненаблюдаемый случайный эффект, общий для всех значений в группе j , а ε _ij — ненаблюдаемый шумовой термин. Для идентификации модели предполагается, что α _j и ε _ij имеют нулевое ожидаемое значение и не коррелируют друг с другом. Кроме того, α _j предполагается, что одинаково распределены, а ε _ij считаются одинаково распределенными. Дисперсия α _j обозначается σ ²
_α , а дисперсия ε _ij обозначается σ ²
_эх .

Популяционный ICC в этой системе равен

${\frac {\sigma _{\alpha }^{2}}{\sigma _{\alpha }^{2}+\sigma _{\varepsilon }^{2}}}.$

В этой системе ICC представляет собой корреляцию двух наблюдений из одной группы.

показывать

[Доказательство]

For a one-way random effects model:

$Y_{ij}=\mu +\alpha _{i}+\epsilon _{ij}$

$\alpha _{i}\sim N(0,\sigma _{\alpha }^{2})$, $\epsilon _{ij}\sim N(0,\sigma _{\varepsilon }^{2})$, $\alpha _{i}$s and $\epsilon _{ij}$s independent and $\alpha _{i}$s are independent from $\epsilon _{ij}$s.

The variance of any observation is: $Var(Y_{ij})=\sigma _{\varepsilon }^{2}+\sigma _{\alpha }^{2}$The covariance of two observations from the same group $i$ (for $j\neq k$) is:

${\begin{aligned}{\text{Cov}}(Y_{ij},Y_{ik})&={\text{Cov}}(\mu +\alpha _{i}+\epsilon _{ij},\mu +\alpha _{i}+\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i}+\epsilon _{ij},\alpha _{i}+\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i},\alpha _{i})+2{\text{Cov}}(\alpha _{i},\epsilon _{ik})+{\text{Cov}}(\epsilon _{ij},\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i},\alpha _{i})\\&={\text{Var}}(\alpha _{i})\\&=\sigma _{\alpha }^{2}.\\\end{aligned}}$

In this, we've used properties of the covariance.

Put together we get:${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma _{\varepsilon }^{2}+\sigma _{\alpha }^{2}}}$

Преимущество этой структуры ANOVA заключается в том, что разные группы могут иметь разное количество значений данных, что сложно обработать с использованием более ранней статистики ICC. Этот ICC всегда неотрицательен, что позволяет интерпретировать его как долю общей дисперсии «между группами». Этот ICC можно обобщить, чтобы учесть ковариатные эффекты, и в этом случае ICC интерпретируется как фиксирующий внутриклассовое сходство значений данных с поправкой на ковариат.

Это выражение никогда не может быть отрицательным (в отличие от исходной формулы Фишера), и поэтому в выборках из популяции, у которой ICC равен 0, ICC в выборках будет выше, чем ICC популяции.

Был предложен ряд различных статистических данных ICC, не все из которых оценивают один и тот же параметр населения. Были серьезные споры о том, какие статистические данные ICC подходят для конкретного использования, поскольку они могут давать совершенно разные результаты для одних и тех же данных.

Связь с коэффициентом корреляции Пирсона

По своей алгебраической форме первоначальный ICC Фишера больше всего напоминает коэффициент корреляции Пирсона . Одно ключевое различие между этими двумя статистическими данными заключается в том, что в ICC данные центрируются и масштабируются с использованием объединенного среднего и стандартного отклонения, тогда как в корреляции Пирсона каждая переменная центрируется и масштабируется по своему собственному среднему и стандартному отклонению. Такое объединенное масштабирование для ICC имеет смысл, поскольку все измерения имеют одинаковую величину (хотя и для единиц в разных группах). Например, в парном наборе данных, где каждая «пара» представляет собой одно измерение, выполненное для каждой из двух единиц (например, взвешивание каждого близнеца в паре однояйцевых близнецов), а не два разных измерения для одной единицы (например, измерение роста и вес для каждого человека), ICC является более естественным показателем связи, чем корреляция Пирсона.

Важным свойством корреляции Пирсона является то, что она инвариантна к применению отдельных линейных преобразований к двум сравниваемым переменным. Таким образом, если мы соотносим X и Y , где, скажем, Y = 2 X + 1, корреляция Пирсона между X и Y равна 1 — идеальная корреляция. Это свойство не имеет смысла для ICC, поскольку нет основы для принятия решения о том, какое преобразование применить к каждому значению в группе. Однако если все данные во всех группах подвергнуть одному и тому же линейному преобразованию, ICC не изменится.

Использование при оценке соответствия среди наблюдателей.

ICC используется для оценки последовательности или соответствия измерений, выполненных несколькими наблюдателями, измеряющими одну и ту же величину. Например, если нескольких врачей попросят оценить результаты компьютерной томографии на наличие признаков прогрессирования рака, мы можем спросить, насколько эти оценки соответствуют друг другу. Если правда известна (например, если компьютерная томография проводилась на пациентах, которые впоследствии перенесли диагностическую операцию), то основное внимание обычно будет уделяться тому, насколько оценки врачей соответствуют истине. Если истина неизвестна, мы можем рассматривать только сходство результатов. Важным аспектом этой проблемы является то, что существует вариабельность как между наблюдателями , так и внутри наблюдателя. Вариабельность между наблюдателями относится к систематическим различиям между наблюдателями — например, один врач может постоянно относить пациентов к более высокому уровню риска, чем другие врачи. Вариабельность внутри наблюдателя относится к отклонениям оценки конкретного наблюдателя у конкретного пациента, которые не являются частью систематической разницы.

ICC создан для применения к взаимозаменяемым измерениям, то есть сгруппированным данным, в которых нет значимого способа упорядочить измерения внутри группы. Если при оценке соответствия среди наблюдателей одни и те же наблюдатели оценивают каждый изучаемый элемент, то, вероятно, будут существовать систематические различия между наблюдателями, что противоречит идее взаимозаменяемости. Если ICC используется в ситуации, когда существуют систематические различия, результатом является составная мера изменчивости внутри и между наблюдателями. Одной из ситуаций, когда разумно можно предположить, что взаимозаменяемость сохраняется, является ситуация, когда образец, подлежащий оценке, скажем, образец крови, делится на несколько аликвот, и эти аликвоты измеряются отдельно на одном и том же приборе. В этом случае возможность замены будет сохраняться до тех пор, пока не будет наблюдаться влияние последовательности анализа проб.

Поскольку коэффициент внутриклассовой корреляции представляет собой совокупность изменчивости внутри наблюдателя и между наблюдателями, его результаты иногда считаются трудными для интерпретации, когда наблюдатели не взаимозаменяемы. Коэна Альтернативные меры, такие как статистика каппы , каппа Флейсса и коэффициент корреляции согласия. были предложены в качестве более подходящей меры согласия между необменными наблюдателями.

Расчет в пакетах программ

Различные определения коэффициента внутриклассовой корреляции применялись к трем сценариям согласия между наблюдателями.

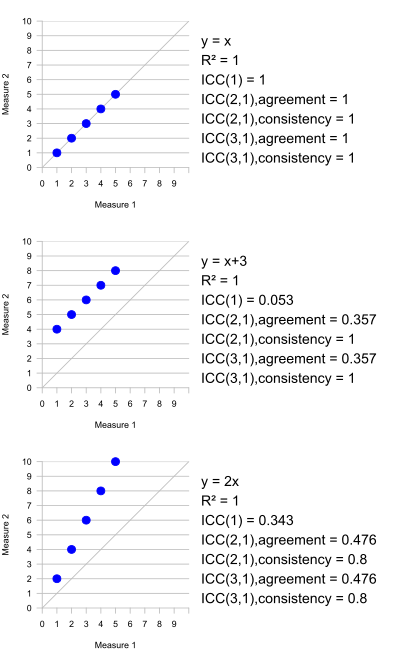
ICC поддерживается в пакете программного обеспечения с открытым исходным кодом R (с использованием функции «icc» в пакетах psy или irr или через функцию «ICC» в пакете psych .) rptR Пакет предоставляет методы оценки ICC и повторяемости для данных с гауссовским, биномиальным и пуассоновским распределением в рамках смешанной модели. Примечательно, что пакет позволяет оценивать скорректированный ICC (т. е. контролировать другие переменные) и вычисляет доверительные интервалы на основе параметрической начальной загрузки и значимости на основе перестановки остатков. Коммерческое программное обеспечение также поддерживает ICC, например Stata или SPSS.

Различные типы ICC [3]. Архивировано 3 марта 2009 г. в Wayback Machine.

Конвенция Шраута и Фляйсса	Конвенция Макгроу и Вонга	Имя в SPSS и Stata
ИКЦ(1,1)	Односторонний случайный выбор, одинарный балл ICC(1)	Односторонние случайные, одиночные измерения
ИКЦ(2,1)	Двусторонний случайный выбор, одинарный балл ICC(A,1)	Двусторонняя случайность, отдельные измерения, абсолютное согласие
ИКЦ(3,1)	Двусторонняя смешанная оценка, одинарная оценка ICC(C,1)	Двустороннее смешанное измерение, отдельные меры, последовательность
неопределенный	Двусторонний случайный выбор, одинарный балл ICC(C,1)	Двусторонняя случайность, одиночные измерения, последовательность
неопределенный	Двусторонняя смешанная оценка, одинарная оценка ICC(A,1)	Двустороннее смешанное, отдельные меры, абсолютное согласие
ИКЦ(1,к)	Односторонний случайный результат, средний балл ICC(k)	Односторонние случайные, средние меры
ИКЦ(2,к)	Двусторонний случайный выбор, средний балл ICC(A,k)	Двусторонняя случайность, средние показатели, абсолютное согласие
ИКЦ(3,к)	Двустороннее смешанное, средний балл ICC(C,k)	Двустороннее смешанное измерение, средние показатели, последовательность
неопределенный	Двусторонний случайный выбор, средний балл ICC(C,k)	Двусторонняя случайность, средние показатели, последовательность
неопределенный	Двусторонняя смешанная оценка, средний балл ICC(A,k)	Двустороннее смешанное измерение, средние показатели, абсолютное согласие

Эти три модели:

• Односторонние случайные эффекты: каждый испытуемый оценивается разными наборами из k случайно выбранных оценщиков;
• Двусторонняя случайность: случайным образом выбираются k оценщиков, затем каждый испытуемый оценивается одним и тем же набором k оценщиков;
• Двустороннее смешанное: определены k фиксированных оценщиков. Каждый предмет оценивается k оценщиками.

Количество измерений:

• Одиночные измерения: даже если в эксперименте проводится более одного измерения, надежность применяется к контексту, где будет выполняться одно измерение одного оценщика;
• Средние показатели: надежность применяется к контексту, где показатели k оценщиков будут усредняться по каждому предмету.

Последовательность или абсолютное согласие:

• Абсолютное согласие: представляет интерес согласие между двумя оценщиками, включая систематические ошибки обоих оценщиков и случайные остаточные ошибки;
• Согласованность: в контексте повторных измерений одним и тем же оценщиком систематические ошибки оценщика аннулируются и сохраняется только случайная остаточная ошибка.

Согласованность ICC не может быть оценена в модели односторонних случайных эффектов, поскольку нет способа разделить межэкспертные и остаточные дисперсии.

Обзор и повторный анализ трех моделей для отдельных показателей ICC с альтернативным рецептом их использования также были представлены Liljequist et al. (2019).

Интерпретация

Чикетти (1994) дает следующие часто цитируемые рекомендации по интерпретации каппа показателей межоценочного соглашения или ICC:

• Менее 0,40 – плохо.
• Между 0,40 и 0,59 — удовлетворительно.
• Между 0,60 и 0,74 — хорошо.
• Между 0,75 и 1,00 — отлично.

Другое руководство дано Ку и Ли (2016):

• ниже 0,50: плохо
• от 0,50 до 0,75: умеренный
• от 0,75 до 0,90: хорошо
• выше 0,90: отлично

См. также

• Коэффициент корреляции
• Эффект дизайна
• Размер эффекта#Эта-квадрат (η2)

Ссылки

Другие

• Сравнение двух показателей коэффициента внутриклассовой корреляции

Внешние ссылки

• AgreeStat 360: облачный анализ надежности между экспертами, каппа Коэна, AC1/AC2 Гвета, альфа Криппендорфа, Бреннан-Предигер, обобщенная каппа Фляйсса, коэффициенты внутриклассовой корреляции.
• Полезный онлайн-инструмент, позволяющий рассчитывать различные типы ICC.