Весь график
| Весь график | |
|---|---|
 Весь график | |
| Назван в честь | WT Тутте |
| Вершины | 46 |
| Края | 69 |
| Радиус | 5 |
| Диаметр | 8 |
| Обхват | 4 |
| Автоморфизмы | 3 ( З / 3З ) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Характеристики | Кубический Планарный Многогранник |
| Таблица графиков и параметров | |
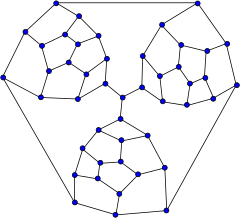
В математической области теории графов граф Тутте — это 3- регулярный граф с 46 вершинами и 69 ребрами, названный в честь У. Т. Тутта . [1] Он имеет хроматическое число 3, хроматический индекс 3, обхват 4 и диаметр 8.
Граф Тутте представляет собой кубический многогранный граф , но не является гамильтоновым . Следовательно, это контрпример к гипотезе Тейта о том, что каждый 3-правильный многогранник имеет гамильтонов цикл. [2]
Опубликованный Тутте в 1946 году, это первый контрпример, построенный для этой гипотезы. [3] Позже были найдены и другие контрпримеры, во многих случаях основанные на теореме Гринберга .
Строительство
[ редактировать ]
Из небольшого плоского графа, называемого фрагментом Тутте, У. Т. Тутте построил негамильтонов многогранник, соединив три таких фрагмента. «Обязательные» ребра фрагментов, которые должны быть частью любого гамильтонова пути через фрагмент, соединяются в центральной вершине; поскольку любой цикл может использовать только два из этих трех ребер, не может быть гамильтонова цикла.
Полученный граф является 3-связным и плоским , поэтому по теореме Стейница это график многогранника. У него 25 граней.
Геометрически его можно реализовать из тетраэдра (грани которого соответствуют четырем большим девятигранным граням на рисунке, три из которых находятся между парами фрагментов, а четвертая образует внешнюю часть) путем многократного усечения трех его вершин .
Алгебраические свойства
[ редактировать ]Группа автоморфизмов графа Тутта — это Z /3 Z , циклическая группа порядка 3.
Характеристический полином графа Тутте:
Связанные графики
[ редактировать ]Хотя граф Тутте является первым открытым 3-регулярным негамильтоновым многогранным графом, он не является самым маленьким из таких графов.
В 1965 году Ледерберг нашел граф Барнетта – Босака – Ледерберга на 38 вершинах. [4] [5] В 1968 году Гринберг построил дополнительные небольшие контрпримеры к гипотезе Тейта – графы Гринберга на 42, 44 и 46 вершинах. [6] В 1974 году Фолкнер и Янгер опубликовали еще два графа — графы Фолкнера–Янгера на 42 и 44 вершинах. [7]
Наконец, Холтон и Маккей показали, что существует ровно шесть негамильтоновых многогранников с 38 вершинами, которые имеют нетривиальные трехреберные разрезы. Они образуются путем замены двух вершин пятиугольной призмы тем же фрагментом, что и в примере Тутте. [8]
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «График Тутте» . Математический мир .
- ^ Тейт, П.Г. Листинга (1884), « Топология », Философский журнал , 5-я серия, 17 : 30–46 . Перепечатано в научных статьях , Vol. II, стр. 85–98.
- ^ Тутте, В.Т. (1946), «О гамильтоновых схемах» (PDF) , Журнал Лондонского математического общества , 21 (2): 98–101, doi : 10.1112/jlms/s1-21.2.98 .
- ^ Ледерберг, Дж. «DENDRAL-64: Система компьютерного построения, подсчета и обозначения органических молекул в виде древовидных структур и циклических графов. Часть II. Топология циклических графов». Промежуточный отчет Национальному управлению по аэронавтике и исследованию космического пространства. Грант NsG 81-60. 15 декабря 1965 года . [1] .
- ^ Вайсштейн, Эрик В. «График Барнетта-Босака-Ледерберга» . Математический мир .
- ^ Гринберг, Э.Дж. «Плоские однородные графы третьей степени без гамильтоновых схем». Латвийская математика. Ежегодник, Издат. Зинатне, Рига, 4, 51–58, 1968.
- ^ Фолкнер, ГБ и Младший, Д.Х. «Негамильтоновы кубические плоские карты». Дискретная математика. 7, 67–74, 1974.
- ^ Холтон, Д.А.; Маккей, Б.Д. (1988), «Наименьшие негамильтоновы 3-связные кубические плоские графы имеют 38 вершин», Journal of Combinatorial Theory, Series B , 45 (3): 305–319, doi : 10.1016/0095-8956 (88) )90075-5 .

