Графовая динамическая система

В математике концепция графовых динамических систем может использоваться для описания широкого спектра процессов, происходящих на графах или в сетях. Основной темой математического и вычислительного анализа ГРС является связь их структурных свойств (например, сетевых связей) и возникающей в результате глобальной динамики.

Работа над GDS рассматривает конечные графы и конечные пространства состояний. Таким образом, исследование обычно включает методы, например, теории графов , комбинаторики , алгебры и динамических систем , а не дифференциальной геометрии. В принципе, можно определить и изучить GDS на бесконечном графе (например, клеточные автоматы или вероятностные клеточные автоматы на бесконечном графе). $\mathbb {Z} ^{k}$ или взаимодействующие системы частиц , когда включена некоторая случайность), а также GDS с бесконечным пространством состояний (например, $\mathbb {R}$ как в связанных решетках карт); см., например, Ву. ^[1] В дальнейшем все неявно предполагается конечным, если не указано иное.

Формальное определение [ править ]

Динамическая система графов состоит из следующих компонентов:

Конечный граф Y с множеством вершин v[ Y ] = {1,2, ... , n}. В зависимости от контекста граф может быть направленным или неориентированным.
Состояние x _v для каждой вершины v графа Y, взятой из конечного множества K . Состояние системы — это n -кортеж x = ( x ₁ , x ₂ , ..., x _n ), а x [ v ] — это кортеж, состоящий из состояний, связанных с вершинами в 1-окрестности v в Y (в некотором фиксированном порядке).
Вершинная функция f _v для каждой вершины v . Функция вершины отображает состояние вершины v в момент времени t в состояние вершины в момент времени t + 1 на основе состояний, связанных с 1-окрестностью вершины v в Y .
Схема обновления, определяющая механизм, с помощью которого выполняется отображение состояний отдельных вершин, чтобы создать дискретную динамическую систему с отображением F : K. ^н → К ^н.

Фазовое пространство , связанное с динамической системой с отображением F : K ^н → К ^н — конечный ориентированный граф с множеством вершин K ^н и направленные ребра ( x , F ( x )). Структура фазового пространства определяется свойствами графа Y , вершинными функциями ( i _и fi) _схемой обновления. Исследования в этой области направлены на вывод свойств фазового пространства на основе структуры компонентов системы. Анализ носит локально-глобальный характер.

Обобщенные клеточные автоматы (ОКА) [ править ]

Если, например, схема обновления состоит из синхронного применения вершинных функций, то получается класс обобщенных клеточных автоматов (ОК). В этом случае глобальное отображение F : K ^н → К ^н дается

$F(x)_{v}=f_{v}(x[v])\;.$

Этот класс называется обобщенными клеточными автоматами, поскольку классические или стандартные клеточные автоматы обычно определяются и изучаются на регулярных графах или сетках, а вершинные функции обычно считаются идентичными.

Пример: пусть Y — круговой граф на вершинах {1,2,3,4} с ребрами {1,2}, {2,3}, {3,4} и {1,4}, обозначаемый Circ ₄ . Пусть K = {0,1} — пространство состояний для каждой вершины и используйте функцию nor ₃ : K ³ → K определяется как nor ₃ ( x,y,z ) = (1 + x )(1 + y )(1 + z ) с арифметикой по модулю 2 для всех вершинных функций. Затем, например, состояние системы (0,1,0,0) сопоставляется с (0, 0, 0, 1) с использованием синхронного обновления. Все переходы показаны в фазовом пространстве ниже.

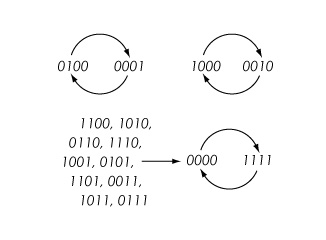
Последовательные динамические системы (СДС) [ править ]

Если вершинные функции применяются асинхронно в последовательности, заданной словом w = ( w ₁ , w ₂ , ... , w _m ) или перестановкой $\pi$ = ( $\pi _{1}$ , $\pi _{2},\dots ,\pi _{n}$ ) v [ Y ] получаем класс последовательных динамических систем (СДС). ^[2] В этом случае удобно ввести Y -локальные отображения F _i, построенные из вершинных функций по формуле

F_{i}(x)=(x_{1},x_{2},\ldots ,x_{i-1},f_{i}(x[i]),x_{i+1},\ldots ,x_{n})\;.

Отображение SDS F = [ F _Y , w ] : K ^н → К ^н это функциональная композиция

[F_{Y},w]=F_{w(m)}\circ F_{w(m-1)}\circ \cdots \circ F_{w(2)}\circ F_{w(1)}\;.

Если последовательность обновления представляет собой перестановку, часто говорят о SDS перестановки, чтобы подчеркнуть этот момент.

Пример: пусть Y — круговой граф на вершинах {1,2,3,4} с ребрами {1,2}, {2,3}, {3,4} и {1,4}, обозначаемый Circ ₄ . Пусть K = {0,1} — пространство состояний для каждой вершины и используйте функцию nor ₃ : K ³ → K определяется как nor ₃ ( x, y, z ) = (1 + x )(1 + y )(1 + z ) с арифметикой по модулю 2 для всех вершинных функций. Используя последовательность обновления (1,2,3,4), состояние системы (0, 1, 0, 0) сопоставляется с (0, 0, 1, 0). Все переходы состояний системы для этой последовательной динамической системы показаны в фазовом пространстве ниже.

Стохастические графовые динамические системы [ править ]

Например, с точки зрения приложений интересно рассмотреть случай, когда один или несколько компонентов GDS содержат стохастические элементы. Мотивирующие приложения могут включать процессы, которые не до конца понятны (например, динамика внутри клетки) и в которых определенные аспекты для всех практических целей, по-видимому, ведут себя в соответствии с некоторым распределением вероятностей. Существуют также приложения, основанные на детерминистских принципах, описание которых настолько сложно и громоздко, что имеет смысл рассмотреть вероятностные аппроксимации.

Каждый элемент графовой динамической системы можно сделать стохастическим несколькими способами. Например, в последовательной динамической системе последовательность обновления может быть сделана стохастической. На каждом шаге итерации можно выбрать последовательность обновления w случайным образом из заданного распределения последовательностей обновления с соответствующими вероятностями. Соответствующее вероятностное пространство последовательностей обновлений порождает вероятностное пространство карт SDS. Естественным объектом для изучения в этом отношении является цепь Маркова в пространстве состояний, индуцированная этим набором карт SDS. Этот случай называется стохастической GDS последовательности обновления и мотивируется, например, процессами, в которых «события» происходят случайным образом в соответствии с определенными скоростями (например, химические реакции), синхронизацией в параллельных вычислениях/дискретном моделировании событий, а также в вычислительных парадигмах, описанных позже. .

Этот конкретный пример со стохастической последовательностью обновления иллюстрирует два общих факта для таких систем: переход к динамической системе со стохастическим графом обычно приводит к (1) изучению цепей Маркова (со специфической структурой, определяемой компонентами GDS) и (2) полученные цепи Маркова имеют тенденцию быть большими и иметь экспоненциальное число состояний. Основная цель изучения стохастической GDS — получить возможность создавать сокращенные модели.

Можно также рассмотреть случай, когда вершинные функции стохастические, т.е. функция стохастическая GDS . Например, случайные логические сети являются примерами стохастической функции GDS, использующей схему синхронного обновления и где пространство состояний равно K = {0, 1}. Конечно- вероятностные клеточные автоматы (PCA) - еще один пример функции стохастической GDS. В принципе класс взаимодействующих систем частиц (IPS) охватывает конечные и бесконечные PCA , но на практике работа над IPS в основном связана с бесконечным случаем, поскольку это позволяет вводить более интересные топологии в пространстве состояний.

Приложения [ править ]

Динамические графовые системы представляют собой естественную основу для описания распределенных систем, таких как биологические сети и эпидемии в социальных сетях, многие из которых часто называют сложными системами.

См. также [ править ]

Ссылки [ править ]

^ Ву, Чай Ва (2005). «Синхронизация в сетях нелинейных динамических систем, связанных ориентированным графом». Нелинейность . 18 (3): 1057–1064. Бибкод : 2005Nonli..18.1057W . дои : 10.1088/0951-7715/18/3/007 . S2CID 122111995 .
^ Мортвейт, Хеннинг С.; Рейдис, Кристиан М. (2008). Введение в последовательные динамические системы . Университеттекст. Нью-Йорк: Springer Verlag . ISBN 978-0-387-30654-4 .

Дальнейшее чтение [ править ]

Маколи, Мэтью; Мортвейт, Хеннинг С. (2009). «Циклическая эквивалентность графовых динамических систем». Нелинейность . 22 (2): 421–436. arXiv : 0802.4412 . Бибкод : 2009Nonli..22..421M . дои : 10.1088/0951-7715/22/2/010 . S2CID 17978550 .
Голубицкий, Мартин ; Стюарт, Ян (2003). Перспектива симметрии . Базель: Биркхаузер. ISBN 0-8176-2171-7 .

Внешние ссылки [ править ]

Графовые динамические системы - математическая основа для систем, основанных на взаимодействии, их анализ и моделирование, Хеннинг Мортвейт

[wu-05-1] Ву, Чай Ва (2005). «Синхронизация в сетях нелинейных динамических систем, связанных ориентированным графом». Нелинейность . 18 (3): 1057–1064. Бибкод : 2005Nonli..18.1057W . дои : 10.1088/0951-7715/18/3/007 . S2CID 122111995 .

[Mortveit-08-2] Мортвейт, Хеннинг С.; Рейдис, Кристиан М. (2008). Введение в последовательные динамические системы . Университеттекст. Нью-Йорк: Springer Verlag . ISBN 978-0-387-30654-4 .

[1]

[2]