Булева задача о тройках Пифагора
Проблема булевых пифагоровых троек — это задача из теории Рэмсея о том, положительные целые числа можно ли раскрасить в красный и синий цвета так, чтобы ни одна пифагорейская тройка не состояла только из красных или всех синих членов. Проблема булевых троек Пифагора была решена Мариной Хойле , Оливером Куллманном и Виктором В. Мареком в мае 2016 года с помощью компьютерного доказательства . [1]
Заявление [ править ]
Задача состоит в том, можно ли раскрасить каждое из натуральных чисел в красный или синий цвет так, чтобы не было пифагоровой тройки целых чисел a , b , c , удовлетворяющей все одного цвета.
Например, в пифагорейской тройке 3, 4 и 5 ( ), если 3 и 4 окрашены в красный цвет, то 5 необходимо покрасить в синий цвет.
Решение [ править ]
Марин Хойле , Оливер Куллманн и Виктор В. Марек показали, что такая раскраска возможна только до числа 7824. Фактическое утверждение доказанной теоремы таково:
Теорема . Множество {1, . . . , 7824} можно разбить на две части так, чтобы ни одна часть не содержала пифагорову тройку, а для {1, . . . , 7825}. [2]
Есть 2 7825 ≈ 3.63×10 2355 возможные цветовые комбинации для чисел до 7825 . Эти возможные раскраски были логически и алгоритмически сужены примерно до триллиона (все еще очень сложных) случаев, а те, которые были выражены в виде логических задач выполнимости, были исследованы с помощью решателя SAT . Создание доказательства заняло около 4 лет ЦП вычислений в течение двух дней на суперкомпьютере Stampede в Техасском вычислительном центре и привело к созданию пропозиционального доказательства объемом 200 терабайт, которое было сжато до 68 гигабайт.
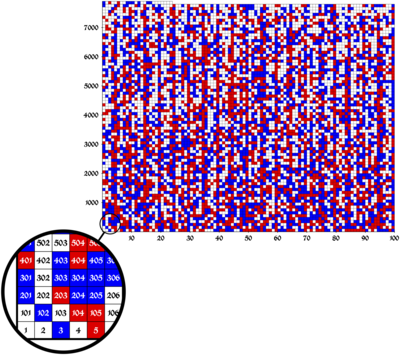
Статья с описанием доказательства была опубликована на конференции SAT 2016. [2] где он получил награду за лучшую бумагу. [3] На рисунке ниже показано возможное семейство раскрасок для набора {1,...,7824} без монохроматической пифагоровой тройки, а белые квадраты можно раскрасить в красный или синий цвет, при этом удовлетворяя этому условию.
Приз [ править ]
В 1980-х годах Рональд Грэм предложил за решение задачи премию в 100 долларов, которая теперь присуждена Марин Хойле . [1]
Обобщения [ править ]
По состоянию на 2018 год проблема все еще открыта для более чем двух цветов, то есть если существует k -раскраска ( k ≥ 3) натуральных чисел такая, что ни одна пифагорова тройка не имеет одного цвета. [4]
См. также [ править ]
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б Лэмб, Эвелин (26 мая 2016 г.). «Доказательство по математике объемом в двести терабайт — самое большое за всю историю» . Природа . 534 (7605): 17–18. Бибкод : 2016Natur.534...17L . дои : 10.1038/nature.2016.19990 . ПМИД 27251254 .
- ↑ Перейти обратно: Перейти обратно: а б Хойле, Марин Дж. Х.; Куллманн, Оливер; Марек, Виктор В. (2016). «Решение и проверка булевой задачи о тройках Пифагора с помощью Cube and Conquer». В Креньу, Надя; Ле Берр, Даниэль (ред.). Теория и приложения тестирования выполнимости – SAT 2016: 19-я Международная конференция, Бордо, Франция, 5-8 июля 2016 г., Материалы . Конспекты лекций по информатике. Том. 9710. стр. 228–245. arXiv : 1605.00723 . дои : 10.1007/978-3-319-40970-2_15 .
- ^ СБ 2016 г.
- ^ Элиаху, Шалом; Фромантен, Жан; Мэрион-Поти, Вирджиния; Робильярд, Денис (2 октября 2018 г.). «Неизбежны ли монохроматические пифагоровы тройки при морфических раскрасках?» . Экспериментальная математика . 27 (4): 419–425. arXiv : 1605.00859 . дои : 10.1080/10586458.2017.1306465 . ISSN 1058-6458 . S2CID 19035265 .

