Теорема Берри – Эссея

В теории вероятностей центральная предельная теорема утверждает, что при определенных обстоятельствах распределение вероятностей масштабированного среднего случайной выборки сходится к нормальному распределению по мере увеличения размера выборки до бесконечности. При более сильных предположениях теорема Берри-Эссеена или неравенство Берри-Эссеена дает более количественный результат, поскольку она также определяет скорость, с которой происходит эта сходимость, давая оценку максимальной ошибки аппроксимации между нормальным распределением и истинное распределение масштабированного выборочного среднего. Приближение измеряется расстоянием Колмогорова–Смирнова . В случае независимых выборок скорость сходимости равна n ^−1/2 , где n — размер выборки, а константа оценивается через третий абсолютный нормированный момент .

Формулировка теоремы

Формулировки теоремы различаются, поскольку она была независимо открыта двумя математиками , Эндрю К. Берри (в 1941 году) и Карлом-Густавом Эссеном (1942), которые затем вместе с другими авторами неоднократно уточняли ее в течение последующих десятилетий.

Одинаково распределенные слагаемые

Одна из версий, несколько жертвующая общностью ради ясности, состоит в следующем:

Существует положительная константа C такая, что если X ₁ , X ₂ , ... являются iid случайными величинами с E ( X ₁ ) = 0, E( X ₁ ² ) = п ² > 0 и E(| X ₁ | ³ ) = ρ < ∞, и если мы определим

$Y_{n}={X_{1}+X_{2}+\cdots +X_{n} \over n}$

выборочное среднее , где F _n — кумулятивная распределения функция

${Y_{n}{\sqrt {n}} \over {\sigma }},$

кумулятивная функция распределения стандартного нормального распределения , тогда для всех x и n и Φ —

$\left|F_{n}(x)-\Phi (x)\right|\leq {C\rho \over \sigma ^{3}{\sqrt {n}}}.\ \ \ \ (1)$

Иллюстрация различия кумулятивных функций распределения, упомянутых в теореме.

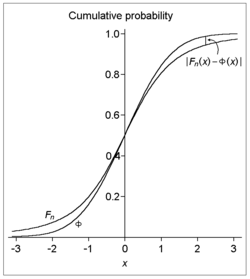
То есть: при наличии последовательности независимых и одинаково распределенных случайных величин , каждая из которых имеет нулевое среднее и положительную дисперсию , если дополнительно третий абсолютный момент конечен, то кумулятивные функции распределения стандартизованного выборочного среднего и стандартного нормального распределения различаются (по вертикали, на графике) не более чем на указанную сумму. что ошибка аппроксимации для всех n (а значит, и предельная скорость сходимости при достаточно большом неопределенном n ) ограничена порядком n Заметим , ^−1/2 .

Рассчитанные верхние границы константы C с годами заметно уменьшились по сравнению с первоначальным значением 7,59, данным Эссеном в 1942 году. Оценка C < 0,4748 следует из неравенства

$\sup _{x\in \mathbb {R} }\left|F_{n}(x)-\Phi (x)\right|\leq {0.33554(\rho +0.415\sigma ^{3}) \over \sigma ^{3}{\sqrt {n}}},$

поскольку п ³ ≤ ρ и 0,33554 · 1,415 < 0,4748. Однако если ρ ≥ 1,286 с ³ , то оценка

$\sup _{x\in \mathbb {R} }\left|F_{n}(x)-\Phi (x)\right|\leq {0.3328(\rho +0.429\sigma ^{3}) \over \sigma ^{3}{\sqrt {n}}},$

еще теснее.

Эссин (1956) доказал, что константа также удовлетворяет нижней границе

$C\geq {\frac {{\sqrt {10}}+3}{6{\sqrt {2\pi }}}}\approx 0.40973\approx {\frac {1}{\sqrt {2\pi }}}+0.01079.$

Неидентично распределенные слагаемые

Пусть X ₁ , X ₂ , ..., независимые случайные величины с E ( X _i ) = 0, E ( X _i ² ) = σ _я ² > 0 и E(| X _i | ³ ) = ρi _< ∞. Кроме того, пусть

$S_{n}={X_{1}+X_{2}+\cdots +X_{n} \over {\sqrt {\sigma _{1}^{2}+\sigma _{2}^{2}+\cdots +\sigma _{n}^{2}}}}$

— нормализованная n -я частичная сумма. Обозначим Fn _— функцию распределения Sn Φ — _{, а} функцию распределения стандартного нормального распределения . Для удобства обозначим

${\vec {\sigma }}=(\sigma _{1},\ldots ,\sigma _{n}),\ {\vec {\rho }}=(\rho _{1},\ldots ,\rho _{n}).$

В 1941 году Эндрю Берри доказал, что для всех n существует абсолютная константа C1 _что такая,

$\sup _{x\in \mathbb {R} }\left|F_{n}(x)-\Phi (x)\right|\leq C_{1}\cdot \psi _{1},\ \ \ \ (2)$

где

$\psi _{1}=\psi _{1}{\big (}{\vec {\sigma }},{\vec {\rho }}{\big )}={\Big (}{\textstyle \sum \limits _{i=1}^{n}\sigma _{i}^{2}}{\Big )}^{-1/2}\cdot \max _{1\leq i\leq n}{\frac {\rho _{i}}{\sigma _{i}^{2}}}.$

Независимо, в 1942 году Карл-Густав Эссен доказал, что для всех n существует абсолютная константа C ₀ такая, что

$\sup _{x\in \mathbb {R} }\left|F_{n}(x)-\Phi (x)\right|\leq C_{0}\cdot \psi _{0},\ \ \ \ (3)$

где

$\psi _{0}=\psi _{0}{\big (}{\vec {\sigma }},{\vec {\rho }}{\big )}={\Big (}{\textstyle \sum \limits _{i=1}^{n}\sigma _{i}^{2}}{\Big )}^{-3/2}\cdot \sum \limits _{i=1}^{n}\rho _{i}.$

Легко убедиться, _ψ0 ≤ψ1 _что . В связи с этим обстоятельством неравенство (3) принято называть неравенством Берри–Эссеена, а величину ψ ₀ – дробью Ляпунова третьего порядка. Более того, в случае, когда слагаемые X ₁ , ..., X _n имеют одинаковые распределения

$\psi _{0}=\psi _{1}={\frac {\rho _{1}}{\sigma _{1}^{3}{\sqrt {n}}}},$

и, таким образом, границы, установленные неравенствами (1), (2) и (3), совпадают, кроме константы.

Что касается C ₀ , то, очевидно, остается справедливой нижняя граница, установленная Эссеном (1956) :

$C_{0}\geq {\frac {{\sqrt {10}}+3}{6{\sqrt {2\pi }}}}=0.4097\ldots .$

Нижняя граница точно достигается только для некоторых распределений Бернулли ( см. в Esseen (1956) их явные выражения ).

Верхние границы C ₀ впоследствии были снижены с первоначальной оценки Эссеена 7,59 до 0,5600.

Многомерная версия

Как и в случае с многомерной центральной предельной теоремой , существует многомерная версия теоремы Берри–Эссеена.

Позволять $X_{1},\dots ,X_{n}$ быть независимым $\mathbb {R} ^{d}$-значные случайные векторы, каждый из которых имеет нулевое среднее значение. Писать $S_{n}=\sum _{i=1}^{n}X_{i}$ и предположим $\Sigma _{n}=\operatorname {Cov} [S_{n}]$ является обратимым. Позволять $Z_{n}\sim \operatorname {N} (0,{\Sigma _{n}})$ быть $d$-мерный гауссиан с той же средней и ковариационной матрицей, что и $S_{n}$. Тогда для всех выпуклых множеств $U\subseteq \mathbb {R} ^{d}$,

${\big |}\Pr[S_{n}\in U]-\Pr[Z_{n}\in U]\,{\big |}\leq Cd^{1/4}\gamma _{n}$,

где $C$ является универсальной константой и $\gamma _{n}=\sum _{i=1}^{n}\operatorname {E} {\big [}\|\Sigma _{n}^{-1/2}X_{i}\|_{2}^{3}{\big ]}$ (третья степень L ² норма ).

Зависимость от $d^{1/4}$ считается оптимальным, но может и не быть таковым.

См. также

• Неравенство Чернова
• Серия Эджворта
• Список неравенств
• Список математических теорем
• Неравенство концентрации

Библиография

• Берри, Эндрю К. (1941). «Точность гауссовского приближения суммы независимых переменных» . Труды Американского математического общества . 49 (1): 122–136. дои : 10.1090/S0002-9947-1941-0003498-3 . JSTOR   1990053 .
• Дарретт, Ричард (1991). Вероятность: теория и примеры . Пасифик Гроув, Калифорния: Уодсворт и Брукс/Коул. ISBN   0-534-13206-5 .
• Эссен, Карл-Густав (1942). «О пределе погрешности Ляпунова в теории вероятностей». Архивы по математике, астрономии и физике . А28 : 1–19. ISSN   0365-4133 .
• Эссен, Карл-Густав (1956). «Моментное неравенство с применением к центральной предельной теореме». Сканд. Актуариетидскр . 39 : 160–170.
• Феллер, Уильям (1972). Введение в теорию вероятностей и ее приложения, том II (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. ISBN   0-471-25709-5 .
• Королев, В. Ю.; Шевцова, ИГ (2010а). «О верхней оценке абсолютной константы в неравенстве Берри – Эссеена». Теория вероятностей и ее приложения . 54 (4): 638–658. дои : 10.1137/S0040585X97984449 .
• Королев, Виктор; Шевцова, Ирина (2010б). «Улучшение неравенства Берри – Эссеена с применением к Пуассону и смешанным случайным суммам Пуассона». Скандинавский актуарный журнал . 2012 (2): 1–25. arXiv : 0912.2795 . дои : 10.1080/03461238.2010.485370 . S2CID   115164568 .
• Манукян, Эдвард Б. (1986). Современные понятия и теоремы математической статистики . Нью-Йорк: Springer-Verlag. ISBN   0-387-96186-0 .
• Серфлинг, Роберт Дж. (1980). Аппроксимационные теоремы математической статистики . Нью-Йорк: Джон Уайли и сыновья. ISBN   0-471-02403-1 .
• Шевцова, ИГ (2008). «Об абсолютной константе в неравенстве Берри – Эссеена». Сборник статей молодых ученых факультета вычислительной математики и кибернетики (5): 101–110.
• Шевцова, Ирина (2007). «Уточнение верхней границы абсолютной константы в неравенстве Берри – Эссеена». Теория вероятностей и ее приложения . 51 (3): 549–553. дои : 10.1137/S0040585X97982591 .
• Шевцова, Ирина (2010). «Улучшение оценок скорости сходимости в теореме Ляпунова». Доклады Математики . 82 (3): 862–864. дои : 10.1134/S1064562410060062 . S2CID   122973032 .
• Шевцова, Ирина (2011). «Об абсолютных константах в неравенствах типа Берри Эссеена для одинаково распределенных слагаемых». arXiv : 1111.6554 [ мат.PR ].
• Шиганов, И.С. (1986). «Уточнение верхней границы константы в остаточном члене центральной предельной теоремы» . Журнал советской математики . 35 (3): 109–115. дои : 10.1007/BF01121471 . S2CID   120112396 .
• Тюрин И.С. (2009). «О точности гауссова приближения». Доклады Математики . 80 (3): 840–843. дои : 10.1134/S1064562409060155 . S2CID   121383741 .
• Тюрин И.С. (2010). «Улучшение верхних оценок констант в теореме Ляпунова». Российские математические обзоры . 65 (3(393)): 201–202. дои : 10.1070/RM2010v065n03ABEH004688 . S2CID   118771013 .
• ван Бик, П. (1972). «Применение методов Фурье к задаче усиления неравенства Берри – Эссеена» . Журнал теории вероятностей и смежных областей . 23 (3): 187–196. дои : 10.1007/BF00536558 . S2CID   121036017 .
• Золотарев, В.М. (1967). «Усиление неравенства Берри–Эссеена» . Журнал теории вероятностей и смежных областей . 8 (4): 332–342. дои : 10.1007/BF00531598 . S2CID   122347713 .

Внешние ссылки

• Гут, Аллан и Холст Ларс. Карл-Густав Эссен , возвращен в марте. 15, 2004.
• «Неравенство Берри – Эссеена» , Математическая энциклопедия , EMS Press , 2001 [1994]