Обратимое уравнение Хилла

Классическая Моно-Ваймана-Шанже модель кооперативности (MWC) обычно публикуется в необратимой форме. То есть в уравнении скорости нет продуктов, которые могут быть проблематичными для тех, кто хочет построить метаболические модели, поскольку нет продуктов ингибирования. ^{[ 1 ]} Однако серия публикаций Поповой и Селькова ^{[ 2 ]} вывел уравнение скорости MWC для обратимой многосубстратной и многопродуктовой реакции.

Та же проблема относится и к классическому уравнению Хилла , которое почти всегда проявляется в необратимой форме. Хофмейр и Корниш-Боуден впервые опубликовали обратимую форму уравнения Хилла. ^{[ 1 ]} С тех пор уравнение обсуждалось в другом месте. ^{[ 3 ]}^{[ 4 ]} и эта модель также использовалась в ряде кинетических моделей, таких как модель фосфофруктокиназы и гликолитических колебаний в β-клетках поджелудочной железы. ^{[ 5 ]} или модель штамма S. cerevisiae, совместно использующего глюкозу и ксилозу. ^{[ 6 ]} Модель также обсуждается в современных учебниках по кинетике ферментов. ^{[ 7 ]}^{[ 8 ]}

Вывод

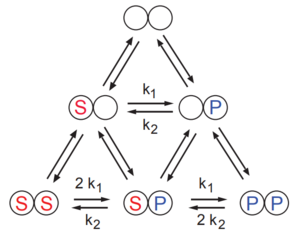
Рассмотрим более простой случай, когда имеется два сайта связывания. См. схему, представленную ниже. Предполагается, что каждый сайт связывает либо молекулу субстрата S, либо продукт P. Каталитическая реакция показана двумя реакциями в основании треугольника схемы, то есть S с P и P с S. Модель предполагает, что этапы связывания всегда в равновесии. Скорость реакции определяется выражением:

$v=k_{1}\left(ES+2ES_{2}+ESP\right)-k_{2}\left(EP+2EP_{2}+ESP\right)$

Применяя предположение о быстром равновесии, мы можем записать различные комплексы в терминах констант равновесия, чтобы получить:

$v={\frac {V_{f}\sigma (1-\rho )(\sigma +\pi )}{1+(\sigma +\pi )^{2}}}$

где $\rho =\Gamma /K_{eq}$ . $\sigma$ и $\pi$ члены представляют собой отношение субстрата и продукта к их соответствующим константам полунасыщения, а именно $\sigma =S/S_{0.5}$ и $\pi =P/P_{0.5}$ и

Используя собственные обозначения автора, если фермент имеет $h$ сайтов, которые могут связывать лиганд, можно показать, что в общем случае форма имеет вид:

$v={\frac {V_{f}\sigma (1-\rho )(\sigma +\pi )^{h-1}}{1+(\sigma +\pi )^{h}}}$

Некооперативное обратимое уравнение Михаэлиса-Ментена можно увидеть, когда мы устанавливаем коэффициент Хилла равным единице.

Если фермент необратим, уравнение превращается в простое уравнение Михаэлиса-Ментен, которое необратимо. При установке константы равновесия на бесконечность уравнение возвращается к более простому случаю, когда произведение препятствует обратному шагу.

Было проведено сравнение MWC и обратимого уравнения Хилла. ^{[ 9 ]}

Модификация обратимого уравнения Хилла была опубликована Вестермарком и др. ^{[ 10 ]} где модификаторы вместо этого повлияли на каталитические свойства. Было показано, что этот вариант гораздо лучше подходит для описания кинетики мышечной фосфофруктокиназы .

Ссылки

^ Jump up to: ^а ^б Хофмейр, Ян-Хендрик С.; Корниш-Боуден, Хофмейр (1997). «Обратимое уравнение Хилла: как включить кооперативные ферменты в метаболические модели» . Биоинформатика . 13 (4): 377–385. дои : 10.1093/биоинформатика/13.4.377 .
^ Попова С.В.; Сельков Э.Е. (15 мая 1975 г.). «Обобщение модели Моно, Ваймана и Чанже на случай обратимой моносубстратной реакции». Письма ФЭБС . 53 (3): 269–273. дои : 10.1016/0014-5793(75)80034-2 .
^ Саа, Педро А.; Нильсен, Ларс К. (декабрь 2017 г.). «Формулирование, построение и анализ кинетических моделей метаболизма: обзор систем моделирования». Достижения биотехнологии . 35 (8): 981–1003. doi : 10.1016/j.biotechadv.2017.09.005 .
^ Либермейстер, Вольфрам; Улендорф, Яннис; Клипп, Эдда (15 июня 2010 г.). «Модульные законы скорости ферментативных реакций: термодинамика, эластичность и реализация» . Биоинформатика . 26 (12): 1528–1534. doi : 10.1093/биоинформатика/btq141 .
^ Вестермарк, Пол О.; Ланснер, Андерс (июль 2003 г.). «Модель фосфофруктокиназы и гликолитических колебаний в β-клетках поджелудочной железы» . Биофизический журнал . 85 (1): 126–139. дои : 10.1016/S0006-3495(03)74460-9 . ПМК 1303071 . ПМИД 12829470 .
^ Мишкович, Любиша; Беал, Йонас; Море, Майкл; Хациманикатис, Василий (20 августа 2019 г.). «Снижение неопределенности в биохимических кинетических моделях: обеспечение желаемых свойств модели» . PLOS Вычислительная биология . 15 (8): e1007242. дои : 10.1371/journal.pcbi.1007242 . ПМК 6716680 . ПМИД 31430276 .
^ Корниш-Боуден, Атель (2012). Основы кинетики ферментов (4., полностью переработанное и значительно дополненное изд.). Вайнхайм: Уайли-Блэквелл. ISBN 978-3-527-33074-4 .
^ Сауро, Герберт М. (2013). Кинетика ферментов для системной биологии (2-е изд.). Нью-Йорк, штат Нью-Йорк: Издательство Ambrosius. ISBN 978-0982477335 .
^ Оливье, Б.Г.; Ровер, Дж. М.; Сноп, Дж.Л.; Хофмейр, Ж.-ХС (2006). «Сравнение регуляторного поведения двух совместных обратимых ферментных механизмов». Труды IEE - Системная биология . 153 (5): 335. doi : 10.1049/ip-syb:20060020 .
^ Вестермарк, Пол; Хеллгрен Коталески, Жанетт; Ланснер, Андерс (2004). «Вывод обратимого уравнения Хилла с модификаторами, влияющими на каталитические свойства» . Труды WSEAS по биологии и биомедицине . 1 : 91–98.

[HofCornRev-1] Jump up to: ^а ^б Хофмейр, Ян-Хендрик С.; Корниш-Боуден, Хофмейр (1997). «Обратимое уравнение Хилла: как включить кооперативные ферменты в метаболические модели» . Биоинформатика . 13 (4): 377–385. дои : 10.1093/биоинформатика/13.4.377 .

[2] Попова С.В.; Сельков Э.Е. (15 мая 1975 г.). «Обобщение модели Моно, Ваймана и Чанже на случай обратимой моносубстратной реакции». Письма ФЭБС . 53 (3): 269–273. дои : 10.1016/0014-5793(75)80034-2 .

[3] Саа, Педро А.; Нильсен, Ларс К. (декабрь 2017 г.). «Формулирование, построение и анализ кинетических моделей метаболизма: обзор систем моделирования». Достижения биотехнологии . 35 (8): 981–1003. doi : 10.1016/j.biotechadv.2017.09.005 .

[4] Либермейстер, Вольфрам; Улендорф, Яннис; Клипп, Эдда (15 июня 2010 г.). «Модульные законы скорости ферментативных реакций: термодинамика, эластичность и реализация» . Биоинформатика . 26 (12): 1528–1534. doi : 10.1093/биоинформатика/btq141 .

[5] Вестермарк, Пол О.; Ланснер, Андерс (июль 2003 г.). «Модель фосфофруктокиназы и гликолитических колебаний в β-клетках поджелудочной железы» . Биофизический журнал . 85 (1): 126–139. дои : 10.1016/S0006-3495(03)74460-9 . ПМК 1303071 . ПМИД 12829470 .

[6] Мишкович, Любиша; Беал, Йонас; Море, Майкл; Хациманикатис, Василий (20 августа 2019 г.). «Снижение неопределенности в биохимических кинетических моделях: обеспечение желаемых свойств модели» . PLOS Вычислительная биология . 15 (8): e1007242. дои : 10.1371/journal.pcbi.1007242 . ПМК 6716680 . ПМИД 31430276 .

[7] Корниш-Боуден, Атель (2012). Основы кинетики ферментов (4., полностью переработанное и значительно дополненное изд.). Вайнхайм: Уайли-Блэквелл. ISBN 978-3-527-33074-4 .

[8] Сауро, Герберт М. (2013). Кинетика ферментов для системной биологии (2-е изд.). Нью-Йорк, штат Нью-Йорк: Издательство Ambrosius. ISBN 978-0982477335 .

[9] Оливье, Б.Г.; Ровер, Дж. М.; Сноп, Дж.Л.; Хофмейр, Ж.-ХС (2006). «Сравнение регуляторного поведения двух совместных обратимых ферментных механизмов». Труды IEE - Системная биология . 153 (5): 335. doi : 10.1049/ip-syb:20060020 .

[10] Вестермарк, Пол; Хеллгрен Коталески, Жанетт; Ланснер, Андерс (2004). «Вывод обратимого уравнения Хилла с модификаторами, влияющими на каталитические свойства» . Труды WSEAS по биологии и биомедицине . 1 : 91–98.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]