Проблема с мышами
В математике задача о мышах — это непрерывная задача преследования-уклонения , в которой считается, что несколько мышей (или насекомых, собак, ракет и т. д.) помещены в углы правильного многоугольника . В классической схеме каждый затем начинает двигаться к своему ближайшему соседу (по часовой стрелке или против часовой стрелки). Часто цель состоит в том, чтобы узнать, в какое время мыши встречаются.
В наиболее распространенной версии мыши начинаются с углов единичного квадрата и движутся с единичной скоростью. В этом случае они встречаются через время в одну единицу, поскольку расстояние между двумя соседними мышами всегда уменьшается со скоростью в одну единицу. В более общем смысле, для правильного многоугольника сторон единичной длины, расстояние между соседними мышами уменьшается со скоростью , поэтому они встречаются через некоторое время . [1] [2]
Путь мышей
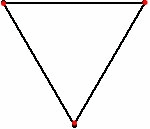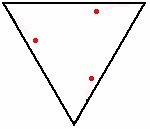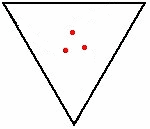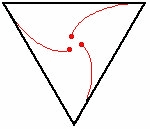
[ редактировать ]Для всех правильных многоугольников каждая мышь чертит кривую преследования в форме логарифмической спирали . Эти кривые встречаются в центре многоугольника. [3]
В СМИ
[ редактировать ]В книге «Дара О Бриэн: Школа твердых сумм» обсуждается проблема с мышами. Вместо 4 мышей используются 4 танцора. [4]
Ссылки
[ редактировать ]- ^ Гамов, Георгий ; Стерн, Марвин (1958). Головоломка Математика . Викинг Пресс. стр. 112–114.
- ^ Лукас, Эдуард (1877). «Проблема трех собак». Нов. Корр. Математика . 3 : 175–176.
- ^ Бернхарт, Артур (1959). «Полигоны преследования». Скрипта Математика . 24 : 23–50. МР 0104178 .
- ^ О Бриайн, Дара; дю Сотуа, Маркус; Уотсон, Марк; Бригсток, Маркус (март 2014 г.). «Счеты Даунтона: математика богатства». Дара О Бриэн: Школа твердых сумм . Сезон 3. Эпизод 4. Прошло 24 минуты. Дэйв.
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Проблема с мышами» . Математический мир .
- Задача Зенона о мышах (муравьях) и логарифмические спирали - лекция на YouTube с выводом уравнений
 | Эта посвященная геометрии, статья, незавершена . Вы можете помочь Википедии, расширив ее . |