Итеративные циклы трафарета

Итеративные трафаретные циклы (ISL) или трафаретные вычисления представляют собой класс решений для числовой обработки данных. ^[1]которые обновляют элементы массива в соответствии с некоторым фиксированным шаблоном, называемым трафаретом. ^[2] Чаще всего они встречаются в компьютерном моделировании , например, для вычислительной гидродинамики в контексте научных и инженерных приложений. Другие известные примеры включают решение уравнений в частных производных , ^[1] ядро Якоби , метод Гаусса–Зейделя , ^[2] обработка изображений ^[1] и клеточные автоматы . ^[3] Регулярная структура массивов отличает трафаретные методы от других методов моделирования, таких как метод конечных элементов . Большинство конечно-разностных кодов , работающих на регулярных сетках, можно сформулировать как ISL.

Определение

ISL выполняют последовательность циклов (называемых временными шагами) по заданному массиву. ^[2] Обычно это двух- или трехмерная регулярная сетка. ^[3] Элементы массивов часто называют ячейками. На каждом временном шаге все элементы массива обновляются. ^[2] Используя соседние элементы массива по фиксированному шаблону (трафарету), вычисляется новое значение каждой ячейки. В большинстве случаев граничные значения остаются неизменными, но в некоторых случаях (например, коды LBM ) их также необходимо корректировать во время вычислений. Поскольку трафарет один и тот же для каждого элемента, схема доступа к данным повторяется. ^[4]

Более формально мы можем определить ISL как пятикортежную структуру. $(I,S,S_{0},s,T)$ со следующим смыслом: ^[3]

$I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ это индексный набор. Он определяет топологию массива.
$S$ — это (не обязательно конечный) набор состояний, одно из которых каждая ячейка может принимать на любом заданном временном шаге.
$S_{0}\colon \mathbb {Z} ^{k}\to S$ определяет начальное состояние системы в момент времени 0.
$s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ Это сам трафарет, который описывает фактическую форму района. Есть $l$ элементы в трафарете.
$T\colon S^{l}\to S$ — это функция перехода, которая используется для определения нового состояния ячейки в зависимости от ее соседей.

Поскольку I представляет собой k -мерный целочисленный интервал, массив всегда будет иметь топологию конечной регулярной сетки. Массив также называют пространством моделирования, а отдельные ячейки идентифицируются по их индексу. $c\in I$ . Трафарет представляет собой упорядоченный набор $l$ относительные координаты. Теперь мы можем получить для каждой ячейки $c$ кортеж индексов его соседей $I_{c}$

I_{c}=\{j\mid \exists x\in s:j=c+x\}\,

Их состояния задаются отображением кортежа $I_{c}$ соответствующему кортежу состояний $N_{i}(c)$ , где $N_{i}\colon I\to S^{l}$ определяется следующим образом:

N_{i}(c)=(s_{1},\ldots ,s_{l}){\text{ with }}s_{j}=S_{i}(I_{c}(j))\,

Это все, что нам нужно для определения состояния системы на следующих временных шагах. $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ с $i\in \mathbb {N}$ :

S_{i+1}(c)={\begin{cases}T(N_{i}(c)),&c\in I\\S_{i}(c),&c\in \mathbb {Z} ^{k}\setminus I\end{cases}}

Обратите внимание, что $S_{i}$ определяется на $\mathbb {Z} ^{k}$ и не только на $I$ поскольку граничные условия тоже необходимо задать. Иногда элементы $I_{c}$ может быть определен путем сложения векторов по модулю размера пространства моделирования для реализации тороидальных топологий:

I_{c}=\{j\mid \exists x\in s:j=((c+x)\mod (n_{1},\ldots ,n_{k}))\}

Это может быть полезно для реализации периодических граничных условий , что упрощает некоторые физические модели.

Пример: 2D-итерация Якоби

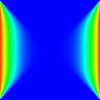
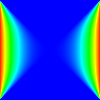
Чтобы проиллюстрировать формальное определение, мы рассмотрим, как Якоби можно определить двумерную итерацию . Функция обновления вычисляет среднее арифметическое четырех соседей ячейки. В этом случае мы начинаем с начального решения, равного 0. Левая и правая границы фиксируются на уровне 1, а верхняя и нижняя границы устанавливаются на 0. После достаточного количества итераций система сходится к седловидной форме.

{\begin{aligned}I&=[0,\ldots ,99]^{2}\\S&=\mathbb {R} \\S_{0}&:\mathbb {Z} ^{2}\to \mathbb {R} \\S_{0}((x,y))&={\begin{cases}1,&x<0\\0,&0\leq x<100\\1,&x\geq 100\end{cases}}\\s&=((0,-1),(-1,0),(1,0),(0,1))\\T&\colon \mathbb {R} ^{4}\to \mathbb {R} \\T((x_{1},x_{2},x_{3},x_{4}))&=0.25\cdot (x_{1}+x_{2}+x_{3}+x_{4})\end{aligned}}

S_{0}

S_{200}

S_{400}

S_{600}

S_{800}

S_{1000}

2D-итерация Якоби на

100^{2}

Множество

Трафареты

Форма окрестности, используемая при обновлениях, зависит от самого приложения. Наиболее распространенными трафаретами являются 2D или 3D версии окрестности фон Неймана и окрестности Мура . В приведенном выше примере используется 2D-трафарет фон Неймана, тогда как в кодах LBM обычно используется его 3D-вариант. В «Игре жизни Конвея» используется 2D-окрестность Мура. Тем не менее, другие трафареты, такие как 25-точечный трафарет для распространения сейсмических волн, ^[5] тоже можно найти.

9-точечный 2D-трафарет

5-точечный 2D-трафарет

7-point 3D stencil

25-point 3D stencil

Подборка трафаретов, используемых в различных научных приложениях.

Проблемы реализации

Многие коды моделирования могут быть естественным образом сформулированы как ISL. Поскольку время вычислений и потребление памяти растут линейно с увеличением количества элементов массива, параллельная реализация ISL имеет первостепенное значение для исследований. ^[6] Это сложно, поскольку вычисления тесно связаны (из-за того, что обновления ячеек зависят от соседних ячеек), а большинство ISL привязаны к памяти (т. е. соотношение обращений к памяти и вычислений велико). ^[7] Практически все современные параллельные архитектуры были исследованы на предмет эффективного выполнения ISL; ^[8] на данный момент GPGPU . наиболее эффективными оказались ^[9]

Библиотеки

Из-за важности ISL для компьютерного моделирования и их высоких вычислительных требований существует ряд усилий, направленных на создание библиотек многократного использования для поддержки ученых при выполнении вычислений на основе трафаретов. Библиотеки в основном занимаются распараллеливанием, но могут также решать и другие задачи, такие как ввод-вывод, управление и контрольные точки . Их можно классифицировать по API.

Библиотеки на основе патчей

Это традиционный дизайн. Библиотека управляет набором n -мерных скалярных массивов, к которым пользовательская программа может обращаться для выполнения обновлений. Библиотека занимается синхронизацией границ (названной призрачной зоной или ореолом). Преимущество этого интерфейса в том, что пользовательская программа может перебирать массивы в цикле, что упрощает интеграцию устаревшего кода. ^[10]. Недостатком является то, что библиотека не может обрабатывать блокировку кэша (поскольку это приходится делать внутри циклов ^[11])или обертывание API-вызовов для ускорителей (например, через CUDA или OpenCL). Реализации включают Cactus , среду решения физических задач, и waLBerla .

Клеточные библиотеки

Эти библиотеки перемещают интерфейс для обновления отдельных ячеек моделирования: доступны только текущая ячейка и ее соседи, например, с помощью методов получения/установки. Преимущество этого подхода заключается в том, что библиотека может жестко контролировать, какие ячейки и в каком порядке обновляются, что полезно не только для реализации блокировки кэша, ^[9] но также для запуска одного и того же кода на многоядерных процессорах и графических процессорах. ^[12] Этот подход требует от пользователя перекомпиляции исходного кода вместе с библиотекой. В противном случае для каждого обновления ячейки потребуется вызов функции, что серьезно ухудшит производительность. Это возможно только с помощью таких методов, как шаблоны классов или метапрограммирование , что также является причиной того, что этот дизайн встречается только в новых библиотеках. Примерами являются Physis и LibGeoDecomp .

См. также

Ссылки

^ Jump up to: ^а ^б ^с Рот, Джеральд и др. (1997) Труды SC'97: Высокопроизводительные сети и вычисления. Компиляция трафаретов в высокопроизводительном Фортране.
^ Jump up to: ^а ^б ^с ^д Слот, Питер М.А. и др. (28 мая 2002 г.) Вычислительная наука - ICCS 2002: Международная конференция, Амстердам, Нидерланды, 21–24 апреля 2002 г. Материалы, часть I. Страница 843. Издательство: Springer. ISBN 3-540-43591-3 .
^ Jump up to: ^а ^б ^с Фей, Дитмар и др. (2010) Грид-вычисления: базовая технология вычислительной науки . Страница 439. Издательство: Springer. ISBN 3-540-79746-7
^ Ян, Лоуренс Т.; Го, Миньи. (12 августа 2005 г.) Высокопроизводительные вычисления: парадигма и инфраструктура. Стр. 221. Издательство: Wiley-Interscience. ISBN 0-471-65471-X
^ Мицикявичюс, Паулюс и др. (2009) 3D-вычисление конечных разностей на графических процессорах с использованием CUDA Материалы 2-го семинара по обработке данных общего назначения на графических процессорах ISBN 978-1-60558-517-8
^ Датта, Кошик (2009) Трафаретные коды автонастройки для многоядерных платформ на основе кэша. Архивировано 8 октября 2012 г. на Wayback Machine . доктор философии Диссертация
^ Веллейн, Дж. и др. (2009) Эффективная временная блокировка трафаретных вычислений за счет распараллеливания волнового фронта с учетом многоядерности . 33-я ежегодная Международная конференция IEEE по компьютерному программному обеспечению и приложениям, COMPSAC 2009
^ Датта, Кошик и др. (2008) Оптимизация вычислений трафарета и автоматическая настройка на современных многоядерных архитектурах . SC '08 Материалы конференции ACM/IEEE 2008 г. по суперкомпьютерам
^ Jump up to: ^а ^б Шефер, Андреас и Фей, Дитмар (2011) Высокопроизводительные алгоритмы трафаретного кода для GPGPU , Материалы Международной конференции по вычислительной науке, ICCS 2011.
^ С. Донат, Й. Гетц, К. Файхтингер, К. Иглбергер и У. Рюде (2010) waLBerla: Оптимизация для систем на базе Itanium с тысячами процессоров , Высокопроизводительные вычисления в науке и технике, Гархинг/Мюнхен, 2009 г.
^ Нгуен, Энтони и др. (2010) Оптимизация 3.5-D блокировки для трафаретных вычислений на современных процессорах и графических процессорах , SC '10 Материалы Международной конференции ACM/IEEE 2010 г. по высокопроизводительным вычислениям, сетям, хранению и анализу
^ Наоя Маруяма, Тацуо Номура, Кенто Сато и Сатоши Мацуока (2011) Physis: модель неявно параллельного программирования для трафаретных вычислений на крупномасштабных суперкомпьютерах с графическим ускорением , SC '11 Материалы Международной конференции ACM/IEEE 2011 г. по высокопроизводительным вычислениям, сетям, хранению и анализу

Внешние ссылки

[Roth-1] Jump up to: ^а ^б ^с Рот, Джеральд и др. (1997) Труды SC'97: Высокопроизводительные сети и вычисления. Компиляция трафаретов в высокопроизводительном Фортране.

[Sloot-2] Jump up to: ^а ^б ^с ^д Слот, Питер М.А. и др. (28 мая 2002 г.) Вычислительная наука - ICCS 2002: Международная конференция, Амстердам, Нидерланды, 21–24 апреля 2002 г. Материалы, часть I. Страница 843. Издательство: Springer. ISBN 3-540-43591-3 .

[Fey-3] Jump up to: ^а ^б ^с Фей, Дитмар и др. (2010) Грид-вычисления: базовая технология вычислительной науки . Страница 439. Издательство: Springer. ISBN 3-540-79746-7

[4] Ян, Лоуренс Т.; Го, Миньи. (12 августа 2005 г.) Высокопроизводительные вычисления: парадигма и инфраструктура. Стр. 221. Издательство: Wiley-Interscience. ISBN 0-471-65471-X

[5] Мицикявичюс, Паулюс и др. (2009) 3D-вычисление конечных разностей на графических процессорах с использованием CUDA Материалы 2-го семинара по обработке данных общего назначения на графических процессорах ISBN 978-1-60558-517-8

[Datta-6] Датта, Кошик (2009) Трафаретные коды автонастройки для многоядерных платформ на основе кэша. Архивировано 8 октября 2012 г. на Wayback Machine . доктор философии Диссертация

[Wellein-7] Веллейн, Дж. и др. (2009) Эффективная временная блокировка трафаретных вычислений за счет распараллеливания волнового фронта с учетом многоядерности . 33-я ежегодная Международная конференция IEEE по компьютерному программному обеспечению и приложениям, COMPSAC 2009

[datta2-8] Датта, Кошик и др. (2008) Оптимизация вычислений трафарета и автоматическая настройка на современных многоядерных архитектурах . SC '08 Материалы конференции ACM/IEEE 2008 г. по суперкомпьютерам

[schaefer-9] Jump up to: ^а ^б Шефер, Андреас и Фей, Дитмар (2011) Высокопроизводительные алгоритмы трафаретного кода для GPGPU , Материалы Международной конференции по вычислительной науке, ICCS 2011.

[walberla-10] С. Донат, Й. Гетц, К. Файхтингер, К. Иглбергер и У. Рюде (2010) waLBerla: Оптимизация для систем на базе Itanium с тысячами процессоров , Высокопроизводительные вычисления в науке и технике, Гархинг/Мюнхен, 2009 г.

[35dblocking-11] Нгуен, Энтони и др. (2010) Оптимизация 3.5-D блокировки для трафаретных вычислений на современных процессорах и графических процессорах , SC '10 Материалы Международной конференции ACM/IEEE 2010 г. по высокопроизводительным вычислениям, сетям, хранению и анализу

[physis-12] Наоя Маруяма, Тацуо Номура, Кенто Сато и Сатоши Мацуока (2011) Physis: модель неявно параллельного программирования для трафаретных вычислений на крупномасштабных суперкомпьютерах с графическим ускорением , SC '11 Материалы Международной конференции ACM/IEEE 2011 г. по высокопроизводительным вычислениям, сетям, хранению и анализу

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]