Причинная запись

Эта статья содержит специальные символы . Без надлежащей поддержки рендеринга вы можете увидеть вопросительные знаки, прямоугольники и другие символы .

Причинная нотация — это нотация, используемая для выражения причины и следствия.

В природе и человеческом обществе многие явления имеют причинно-следственные связи, при которых одно явление А (причина) влияет на другое явление Б (следствие). Установление причинно-следственных связей является целью многих научных исследований в различных областях, от биологии ^[1] и физика ^[2] к общественным наукам и экономике . ^[3] Это также является предметом анализа аварий, ^[4] и может считаться предпосылкой для эффективной разработки политики.

Для описания причинно-следственных связей между явлениями распространены неколичественные визуальные обозначения, такие как стрелки, например, в круговороте азота или во многих химических веществах. ^[5]^[6] и математика ^[7] учебники. Также используются математические соглашения, такие как отображение независимой переменной на горизонтальной оси и зависимой переменной на вертикальной оси. ^[8] или обозначение $y=f(x)$ чтобы обозначить, что количество " $y$ "это зависимая переменная, которая является функцией независимой переменной" $x$ ". ^[9] Причинно-следственные связи также описываются с помощью количественных математических выражений. ^[10] (См. раздел «Обозначения» .)

Следующие примеры иллюстрируют различные типы причинно-следственных связей. За ними следуют различные обозначения, используемые для представления причинно-следственных связей.

Примеры

Дальнейшее не обязательно предполагает соглашение, согласно которому $y$ обозначает независимую переменную, а $f(y)$ обозначает функцию независимой переменной $y$ . Вместо, $y$ и $f(y)$ обозначают две величины с априорно неизвестной причинно-следственной связью, которые можно связать математическим выражением.

Пример экосистемы: корреляция без причинно-следственной связи

Представьте себе количество дней с погодой ниже одного градуса Цельсия. $y$ , вызывает образование льда на озере, $f(y)$ , и это заставляет медведей впадать в спячку $g(y)$ . Несмотря на то $g(y)$ не вызывает $f(y)$ и наоборот, можно написать уравнение, связывающее $g(y)$ и $f(y)$ . Это уравнение можно использовать для успешного расчета количества спящих медведей. $g(y)$ , учитывая площадь поверхности озера, покрытую льдом. Однако растапливание льда на участке озера путем посыпания его солью не выведет медведей из спячки. Разбудив медведей физическим беспокойством, лед не растает. В этом случае две величины $f(y)$ и $g(y)$ оба вызваны мешающей переменной $y$ (температура наружного воздуха), но не друг друга. $f(y)$ и $g(y)$ связаны корреляцией без причинно-следственной связи.

Пример из физики: однонаправленная причинно-следственная связь

Предположим, идеальная система, работающая на солнечной энергии, построена так, что если солнечно и солнце обеспечивает интенсивность $I$ из $100$ инцидент в Ваттах на $1$ м $^{2}$ солнечная панель для $10~$ секунды электродвигатель поднимает $2$ кг камня по $50$ метры, $h(I)$ . В более общем смысле мы предполагаем, что система описывается следующим выражением:

$I\times A\times t=m\times g\times h~$ ,

где $I$ представляет интенсивность солнечного света (Дж $\cdot$ с $^{-1}$ $\cdot$ м $^{-2}$ ), $A$ площадь поверхности солнечной панели (м $^{2}$ ), $t$ представляет время (с), $m$ представляет массу (кг), $g$ представляет собой ускорение силы тяжести Земли ( $9.8$ м $\cdot$ с $^{-2}$ ), и $h$ представляет собой высоту, на которую поднимается камень (м).

В этом примере тот факт, что солнечно и есть интенсивность света $I$ , заставляет камень подниматься $h(I)$ , а не наоборот; поднятие камня (увеличение $h(I)$ ) не приведет к включению солнца для освещения солнечной панели (увеличение $I$ ). Причинно-следственная связь между $I$ и $h(I)$ является однонаправленным.

Пример из медицины: две причины для одного результата

Курение, $f(y)$ и воздействие асбеста, $g(y)$ , являются известными причинами рака, $y$ . Можно написать уравнение $f(y)=g(y)$ чтобы описать эквивалентную канцерогенность между тем, сколько сигарет выкуривает человек, $f(y)$ , и сколько граммов асбеста человек вдыхает, $g(y)$ . Здесь ни $f(y)$ причины $g(y)$ ни $g(y)$ причины $f(y)$ , но они оба имеют общий результат.

Пример бартера: двунаправленная причинно-следственная связь

Рассмотрим экономику, основанную на бартере, где количество коров $C$ стоимость того, чем человек владеет, измеряется в стандартной валюте цыплят, $y$ . Кроме того, количество баррелей нефти $B$ ценность, которой владеет человек, может быть измерена в цыплятах, $y$ . Если существует рынок, на котором коров можно обменять на цыплят, которые, в свою очередь, можно обменять на бочки нефти, можно написать уравнение $C(y)=B(y)$ описать ценностные отношения между коровами $C$ и баррели нефти $B$ . Предположим, что человек в этой экономике всегда сохраняет половину своей стоимости в виде коров, а другую половину — в виде баррелей нефти. Затем, увеличивая поголовье коров $C(y)$ предложив им 4 коровы, в конечном итоге приведет к увеличению количества баррелей нефти. $B(y)$ или наоборот. В этом случае математическое равенство $C(y)=B(y)$ описывает двунаправленную причинно-следственную связь.

Обозначения

Химические реакции

В химии многие химические реакции обратимы и описываются с помощью уравнений, стремящихся к динамическому химическому равновесию . В этих реакциях добавление реагента или продукта приводит к протеканию реакции с образованием большего количества продукта или большего количества реагента соответственно. Вместо знака равенства ⇌ принято рисовать стрелки «гарпунного типа», чтобы обозначить обратимый характер реакции и динамическую причинно-следственную связь между реагентами и продуктами. ^[5]^[6]

Статистика: делать обозначения

Do-исчисление , и в частности оператор do, используется для описания причинно-следственных связей на языке вероятности. Например, в do-исчислении используются следующие обозначения: ^[11]

P(Y|do(X))=P(Y)~

,

что можно прочитать как: «вероятность $Y$ учитывая, что ты делаешь $X$ ». Выражение выше описывает случай, когда $Y$ не зависит от чего-либо, сделанного для $X$ . ^[10] Он указывает на то, что не существует однонаправленной причинно-следственной связи, при которой $X$ причины $Y$ .

Причинно-следственные диаграммы

Причинно-следственная диаграмма состоит из набора узлов, которые могут быть связаны или не связаны между собой стрелками. Стрелки между узлами обозначают причинно-следственные связи, причем стрелка указывает от причины к следствию. Существует несколько форм причинных диаграмм, включая диаграммы Исикавы , направленные ациклические графы , диаграммы причинных петель и т. д . ^[10] и графики «почему-потому что» (ГВБ). На изображении ниже показан частичный график «почему-потому», использованный для анализа опрокидывания « Вестника свободного предпринимательства» .

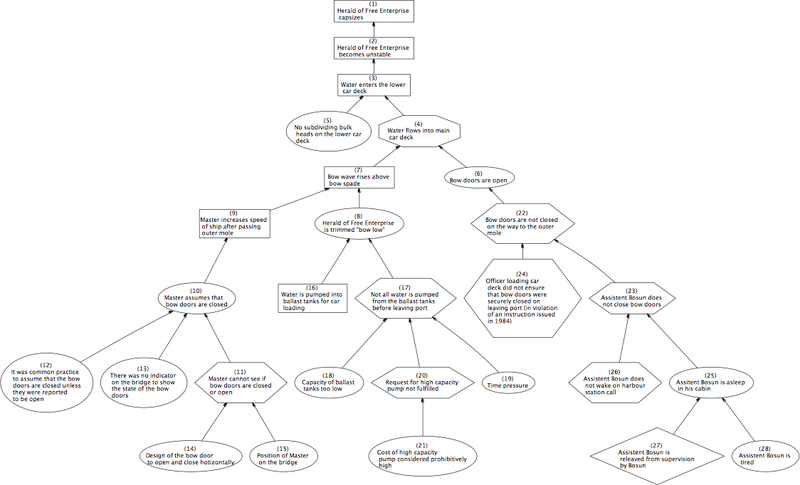
Схемы соединений

Шаблоны соединений можно использовать для описания графовой структуры байесовских сетей. Три возможных шаблона, разрешенных в трехузловом ориентированном ациклическом графе (DAG), включают:

Схемы соединений
Шаблон	Модель
Цепь	$X\rightarrow Y\rightarrow Z$
Вилка	$X\leftarrow Y\rightarrow Z$
Коллайдер	$X\rightarrow Y\leftarrow Z$

Обозначение причинного равенства

Существуют различные формы причинно-следственных связей. Например, две величины $a(s)$ и $b(s)$ оба могут быть вызваны мешающей переменной $s$ , но не друг друга. Представьте себе забастовку мусорщиков в большом городе, $s$ , вызывает усиление запаха мусора, $a(s)$ и увеличение популяции крыс $b(s)$ . Несмотря на то $b(s)$ не вызывает $a(s)$ и наоборот, можно написать уравнение, связывающее $b(s)$ и $a(s)$ . В следующей таблице приведены обозначения, представляющие различные способы, которые $s$ , $a(s)$ и $b(s)$ могут быть связаны друг с другом. ^[12]

Обозначение причинного равенства
Символическое выражение	Определенные отношения между $s$ , $a(s)$ и $b(s)$
$s~{\overset {\rightarrow }{=}}~a\left(s\right)$	$a(s)$ вызвано $s$ . Зависимая переменная $a(s)$ . Независимая переменная $s$ .
$s~{\overset {\leftarrow }{=}}~a\left(s\right)$	$s$ вызвано $a(s)$ . Независимая переменная $a(s)$ . Зависимая переменная $s$ .
$s~{\overset {\leftrightarrow }{=}}~a\left(s\right)$	$a(s)$ и $s$ являются взаимозависимыми или двунаправленно причинными.
$s~{\overset {\rightarrow }{=}}~a\left(s\right)$ $s~{\overset {\rightarrow }{=}}~b\left(s\right)$	Корреляция: $a(s)$ и $b(s)$ оба вызваны $s$ : $a(s)~{\overset {\curvearrowleft \curvearrowright }{=}}~b(s)$ . Если двунаправленная причинно-следственная связь может существовать, но она еще не установлена, используются обозначения $a\left(s\right)~{\overset {\curvearrowleft ?\curvearrowright }{=}}~b\left(s\right)$ можно использовать.
$s~{\overset {\rightarrow }{=}}~a\left(s\right)$ $s~{\overset {\leftarrow }{=}}~b\left(s\right)$	$b(s)$ причины $s~$ что, в свою очередь, вызывает $a(s)$ : $b(s)~{\overset {\rightarrow }{=}}~a(s)$
$s~{\overset {\leftarrow }{=}}~a\left(s\right)$ $s~{\overset {\rightarrow }{=}}~b\left(s\right)$	$a(s)$ причины $s~$ что, в свою очередь, вызывает $g(s)$ : $g(s)~{\overset {\leftarrow }{=}}~a(s)$ .
$s~{\overset {\leftarrow }{=}}~a\left(s\right)$ $s~{\overset {\leftarrow }{=}}~b\left(s\right)$	Неопределенность/двойная причинность: $s~$ может быть вызвано $a(s)$ или $b(s)$ : $a\left(s\right)~{\overset {\curvearrowright \curvearrowleft }{=}}~b\left(s\right)$ , или $b(s)~{\overset {>-<}{=}}~a(s)$
$s~{\overset {\leftrightarrow }{=}}~a\left(s\right)$ $s~{\overset {\rightarrow }{=}}~b\left(s\right)$	$a(s)$ и $s$ являются двунаправленно причинными. $b(s)$ вызвано $a(s)$
$s~{\overset {\rightarrow }{=}}~a\left(s\right)$ $s~{\overset {\leftrightarrow }{=}}~b\left(s\right)$	$b(s)$ и $s$ являются двунаправленно причинными. $a(s)$ вызвано $b(s)$
$s~{\overset {\leftrightarrow }{=}}~a\left(s\right)$ $s~{\overset {\leftrightarrow }{=}}~b\left(s\right)$	$b(s)$ причины $a(s)$ и $a(s)~$ причины $b(s)$ : $a(s)~{\overset {\leftrightarrow }{=}}~b(s)$ . $b(s)$ и $a(s)$ являются двунаправленно причинными.
$s_{1}~{\overset {arb.}{=}}~a\left(s_{1}\right)$ $s_{2}~{\overset {arb.}{=}}~g\left(s_{2}\right)$	Несовпадающие индексы указывают на то, что для любой произвольной причинной связи между $s_{1}$ и $a(s_{1})$ или $s_{2}$ и $b(s_{2})$ , $a(s_{1})$ и $b(s_{2})$ не может быть связано.

Следует предположить, что связь между двумя уравнениями с одинаковым смыслом причинности (например, $s~{\overset {\rightarrow }{=}}~a\left(s\right)$ , и $s~{\overset {\rightarrow }{=}}~b\left(s\right)$ ) представляет собой чистую корреляцию, если не доказано, что оба выражения являются двунаправленными причинными равенствами. В этом случае общая причинно-следственная связь между $b(s)$ и $a(s)$ является двунаправленно причинным.

Ссылки

^ Маршалл, Барри Дж; Уоррен, Дж. Робин (июнь 1984 г.). «Неопознанные изогнутые палочки в желудке больных гастритом и язвенной болезнью». Ланцет . 323 (8390): 1311–1315. дои : 10.1016/S0140-6736(84)91816-6 . ПМИД 6145023 . S2CID 10066001 .
^ Аспект, Ален; Гранжье, Филипп; Роже, Жерар (12 июля 1982 г.). «Экспериментальная реализация мысленного эксперимента Эйнштейна-Подольского-Розена-Бома: новое нарушение неравенств Белла» . Письма о физических отзывах . 49 (2): 91–94. Бибкод : 1982PhRvL..49...91A . doi : 10.1103/PhysRevLett.49.91 .
^ Фишер, Стэнли; Истерли, Уильям (1990). «Экономика государственного бюджетного ограничения». Обозреватель исследований Всемирного банка . 5 (2): 127–142. CiteSeerX 10.1.1.1009.4220 . дои : 10.1093/wbro/5.2.127 .
^ Ладкин, Питер; Лоер, Карстен (апрель 1998 г.). Анализ авиационных происшествий с использованием WB-анализа — применение мультимодального рассуждения (PDF) . Весенний симпозиум. Ассоциация по развитию искусственного интеллекта . Архивировано из оригинала (PDF) 21 декабря 2022 г.
^ Jump up to: ^а ^б Брюс, Паула Юрканис (2007). Органическая химия (5-е изд.). Пирсон Прентис Холл Аппер-Сэддл-Ривер, Нью-Джерси. п. 44,45. ISBN 978-0-13-196316-0 .
^ Jump up to: ^а ^б Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри; Мадура, Джеффри Д. (2007). Общие принципы химии и современные приложения (9-е изд.). Пирсон Прентис Холл Аппер-Сэддл-Ривер, Нью-Джерси. стр. 573–650. ISBN 978-0-13-149330-8 .
^ Б. Джордж, Джордж (2007). Исчисление Томаса (11-е изд.). Пирсон. п. 20. ISBN 978-0-321-18558-7 .
^ Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри; Мадура, Джеффри Д. (2007). Общие принципы химии и современные приложения (9-е изд.). Пирсон Прентис Холл Аппер-Сэддл-Ривер, Нью-Джерси. п. 575. ИСБН 978-0-13-149330-8 .
^ Б. Джордж, Джордж (2007). Исчисление Томаса (11-е изд.). Пирсон. п. 19. ISBN 978-0-321-18558-7 .
^ Jump up to: ^а ^б ^с Перл, Иудея ; Маккензи, Дана (15 мая 2018 г.). Книга «Почему: новая наука о причине и следствии» . Основные книги. ISBN 9780465097616 .
^ {{Хичкок, Кристофер, «Причинные модели», Стэнфордская энциклопедия философии (выпуск весной 2023 г.), Эдвард Н. Залта и Ури Нодельман (ред.), URL = < https://plato.stanford.edu/archives/ spr2023/entries/causal-models/ >}}
^ Ван Хорн Н. и Мукерджи М. Улучшенное описание захваченных ионов как модульной электромеханической системы, J. Appl. Физ. 135, 154401 (2024)

[Marshall1-1] Маршалл, Барри Дж; Уоррен, Дж. Робин (июнь 1984 г.). «Неопознанные изогнутые палочки в желудке больных гастритом и язвенной болезнью». Ланцет . 323 (8390): 1311–1315. дои : 10.1016/S0140-6736(84)91816-6 . ПМИД 6145023 . S2CID 10066001 .

[Aspect1-2] Аспект, Ален; Гранжье, Филипп; Роже, Жерар (12 июля 1982 г.). «Экспериментальная реализация мысленного эксперимента Эйнштейна-Подольского-Розена-Бома: новое нарушение неравенств Белла» . Письма о физических отзывах . 49 (2): 91–94. Бибкод : 1982PhRvL..49...91A . doi : 10.1103/PhysRevLett.49.91 .

[Fischer1-3] Фишер, Стэнли; Истерли, Уильям (1990). «Экономика государственного бюджетного ограничения». Обозреватель исследований Всемирного банка . 5 (2): 127–142. CiteSeerX 10.1.1.1009.4220 . дои : 10.1093/wbro/5.2.127 .

[4] Ладкин, Питер; Лоер, Карстен (апрель 1998 г.). Анализ авиационных происшествий с использованием WB-анализа — применение мультимодального рассуждения (PDF) . Весенний симпозиум. Ассоциация по развитию искусственного интеллекта . Архивировано из оригинала (PDF) 21 декабря 2022 г.

[:4-5] Jump up to: ^а ^б Брюс, Паула Юрканис (2007). Органическая химия (5-е изд.). Пирсон Прентис Холл Аппер-Сэддл-Ривер, Нью-Джерси. п. 44,45. ISBN 978-0-13-196316-0 .

[:5-6] Jump up to: ^а ^б Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри; Мадура, Джеффри Д. (2007). Общие принципы химии и современные приложения (9-е изд.). Пирсон Прентис Холл Аппер-Сэддл-Ривер, Нью-Джерси. стр. 573–650. ISBN 978-0-13-149330-8 .

[:9-7] Б. Джордж, Джордж (2007). Исчисление Томаса (11-е изд.). Пирсон. п. 20. ISBN 978-0-321-18558-7 .

[8] Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри; Мадура, Джеффри Д. (2007). Общие принципы химии и современные приложения (9-е изд.). Пирсон Прентис Холл Аппер-Сэддл-Ривер, Нью-Джерси. п. 575. ИСБН 978-0-13-149330-8 .

[9] Б. Джордж, Джордж (2007). Исчисление Томаса (11-е изд.). Пирсон. п. 19. ISBN 978-0-321-18558-7 .

[:10-10] Jump up to: ^а ^б ^с Перл, Иудея ; Маккензи, Дана (15 мая 2018 г.). Книга «Почему: новая наука о причине и следствии» . Основные книги. ISBN 9780465097616 .

[Hitchcock1-11] {{Хичкок, Кристофер, «Причинные модели», Стэнфордская энциклопедия философии (выпуск весной 2023 г.), Эдвард Н. Залта и Ури Нодельман (ред.), URL = < https://plato.stanford.edu/archives/ spr2023/entries/causal-models/ >}}

[VanHorne2-12] Ван Хорн Н. и Мукерджи М. Улучшенное описание захваченных ионов как модульной электромеханической системы, J. Appl. Физ. 135, 154401 (2024)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]