Алгоритм максимального потока push-relabel

В математической оптимизации алгоритм push-relabel (альтернативно, алгоритм preflow-push ) представляет собой алгоритм вычисления максимальных потоков в потоковой сети . Название «push–relabel» происходит от двух основных операций, используемых в алгоритме. На протяжении всего своего выполнения алгоритм поддерживает «предварительный поток» и постепенно преобразует его в максимальный поток, перемещая поток локально между соседними узлами с помощью операций push под руководством допустимой сети, поддерживаемой операциями перемаркировки . Для сравнения, алгоритм Форда-Фалкерсона выполняет глобальные дополнения, которые направляют поток по путям от источника до приемника. ^{[ 1 ]}

Алгоритм push-relabel считается одним из наиболее эффективных алгоритмов максимального потока. Общий алгоритм имеет сильно полиномиальный $O (V 2 E)$ временная сложность, которая асимптотически более эффективна, чем $O (VE 2)$ Алгоритм Эдмондса–Карпа . ^{[ 2 ]} Конкретные варианты алгоритмов обеспечивают еще меньшую временную сложность. Вариант, основанный на правиле выбора узла с наивысшей меткой, имеет $O (V 2 \sqrt E)$ временная сложность и обычно считается эталоном для алгоритмов максимального потока. ^{[ 3 ]}^{[ 4 ]} Subcubic $O (VE log(V 2 / E))$ Временная сложность может быть достигнута с помощью динамических деревьев , хотя на практике это менее эффективно. ^{[ 2 ]}

Алгоритм push-relabel был расширен для расчета потоков с минимальной стоимостью . ^{[ 5 ]} Идея дистанционных меток привела к более эффективному алгоритму дополняющего пути, который, в свою очередь, можно снова включить в алгоритм push-relabel, чтобы создать вариант с еще более высокой эмпирической эффективностью. ^{[ 4 ]}^{[ 6 ]}

История

Концепция предварительного потока была первоначально разработана Александром В. Карзановым и опубликована в 1974 году в «Советских математических докладах» 15. Этот алгоритм предварительного потока также использовал операцию push; однако для определения того, куда направить поток, вместо системы маркировки использовались расстояния во вспомогательной сети. ^{[ 2 ]}^{[ 7 ]}

Алгоритм push-relabel был разработан Эндрю В. Голдбергом и Робертом Тарджаном . Алгоритм был первоначально представлен в ноябре 1986 года в журнале STOC '86: Труды восемнадцатого ежегодного симпозиума ACM по теории вычислений, а затем официально в октябре 1988 года в виде статьи в журнале ACM. В обеих статьях подробно описана общая форма алгоритма, завершающаяся за $O (V 2 E)$ вместе с $O (V 3)$ последовательная реализация, $O (VE log(V 2 / E))$ реализация с использованием динамических деревьев и параллельная/распределенная реализация. ^{[ 2 ]}^{[ 8 ]} Как поясняется в, ^{[ 9 ]} Гольдберг-Тарьян представил метки расстояний, включив их в параллельный алгоритм максимального потока Йосси Шилоаха и Узи Вишкина . ^{[ 10 ]}

Концепции

Определения и обозначения

Позволять:

$G = (V, E)$ — сеть с функцией емкости $\mathbb {R}$ ,
$F = (G, c, s, t)$ сеть потоков , где $s \in V$ и $t \in V$ выбраны вершины источника и стока соответственно,
$\mathbb {R}$ обозначаем предпоток в $F$ ,
$\mathbb {R}$ обозначаем функцию избытка по отношению к потоку $f$ , определяемую формулой $x f (u) = Σ v \in V f (v, u) - Σ v \in V f (u, v)$ ,
$\mathbb {R}$ обозначают функцию остаточной емкости по отношению к потоку $f$ , определяемую формулой $c f (e) = c (e) - f (e)$ ,
$E f \subset E$ — ребра, где $f < c$ ,

и

$G f (V, E f)$ обозначают сеть G $f$ относительно потока $.$ остаточную

Алгоритм push-relabel использует неотрицательную целочисленную допустимую функцию разметки , которая использует метки расстояний или высоты на узлах, чтобы определить, какие дуги следует выбрать для операции push. Эта функция разметки обозначается $\mathbb {N}$ . Чтобы считаться допустимой, эта функция должна удовлетворять следующим условиям:

Действительная маркировка :

𝓁(ты) \leq 𝓁(v) + 1

для всех

(ты, v) \in E f

Исходное состояние :

𝓁(s) = | V |

Консервация раковины :

𝓁(т) = 0

В алгоритме значения меток $s$ и $t$ фиксированы. $𝓁(u)$ — нижняя граница невзвешенного расстояния от $u$ до $t$ в $G f,$ если $t$ достижимо из $u$ . Если $u$ был отключен от $t$ , то $𝓁(u) - | В |$ — нижняя граница невзвешенного расстояния от $u$ до $s$ . нет $путей s - t,$ В результате, если существует допустимая функция разметки, в $G f$ поскольку ни один такой путь не может быть длиннее $| В | - 1$ .

Дуга $(u, v) \in E f$ называется допустимой, если $𝓁(u) = 𝓁(v) + 1$ . G̃ Допустимая сеть $f (V, Ẽ f) состоит$ из множества $дуг e \in E f$ допустимых . Допустимая сеть является ациклической.

Для фиксированного потока $f$ вершина $v \notin {s, t}$ называется активной , если она имеет положительный эксцесс по отношению к $f$ , т. е. $x f (u) > 0$ .

Операции

Инициализация

Алгоритм начинается с создания остаточного графа, инициализации значений предварительного потока нулевым значением и выполнения набора насыщающих операций push на остаточных дугах $(s, v),$ выходящих из источника, где $v ∈ V \ { s }$ . Аналогично, метки инициализируются так, что метка в источнике представляет собой количество узлов в графе, $𝓁(s) = | В |$ , а всем остальным узлам присваивается нулевая метка. После завершения инициализации алгоритм неоднократно выполняет операции отправки или изменения метки для активных узлов до тех пор, пока не будет выполнена никакая применимая операция.

Толкать

Операция push применяется к допустимой внешней дуге $(u, v)$ активного узла $u$ в $G f$ . Он перемещает $min{x f (u), c f (u, v)}$ единиц потока из $u$ в $v$ .

push(u, v):
    assert x_f[u] > 0 and 𝓁[u] == 𝓁[v] + 1
    Δ = min(x_f[u], c[u][v] - f[u][v])
    f[u][v] += Δ
    f[v][u] -= Δ
    x_f[u] -= Δ
    x_f[v] += Δ

Операция push, которая приводит к тому, что $f (u, v)$ достигает $c (u, v),$ называется насыщающей отправкой , поскольку она использует всю доступную емкость остаточной дуги. В противном случае все лишнее в узле будет перенесено через остаточную дугу. Это называется ненасыщающим или ненасыщающим толчком .

Переименовать

Операция перемаркировки применяется к активному узлу $u,$ который не является ни источником, ни приемником, без каких-либо допустимых исходящих дуг в $G f$ . Он изменяет $𝓁(u)$ так, чтобы оно стало минимальным значением, при котором создается допустимая внешняя дуга. Обратите внимание, что это всегда увеличивает $𝓁(u)$ и никогда не создает крутую дугу, которая представляет собой дугу $(u, v)$ такую, что $c f (u, v) > 0$ и $𝓁(u) > 𝓁(v) + 1$ .

relabel(u):
    assert x_f[u] > 0 and 𝓁[u] <= 𝓁[v] for all v such that c_f[u][v] > 0
    𝓁[u] = 1 + min(𝓁[v] for all v such that c_f[u][v] > 0)

Эффекты push и relabel

После операции push или перемаркировки $𝓁$ остается допустимой функцией разметки относительно $f$ .

Для операции push на допустимой дуге $(u, v)$ она может добавить дугу $(v, u)$ к $E f$ , где $𝓁(v) = 𝓁(u) - 1 \leq 𝓁(u) + 1$ ; он также может удалить дугу $(u, v)$ из $E f$ , где эффективно снимает ограничение $𝓁(u) \leq 𝓁(v) + 1$ .

Чтобы увидеть, что операция изменения метки на узле $u$ сохраняет справедливость $𝓁(u)$ , обратите внимание, что это тривиально гарантируется по определению для исходящих дуг u в $G f$ . Для дуг $u$ в $G f$ увеличенный $𝓁(u)$ может только менее строго удовлетворять ограничениям, но не нарушать их.

Общий алгоритм push-relabel

Общий алгоритм push-relabel используется только в качестве доказательства концепции и не содержит подробностей реализации о том, как выбрать активный узел для операций push и relabel. Эта общая версия алгоритма завершится через $O (V 2 Е)$ .

Поскольку $𝓁(s) = | В |$ , $𝓁(t) = 0$ и нет путей длиннее $| В | - 1$ в $Gf s$ , чтобы $𝓁(s)$ удовлетворяло допустимому условию разметки, $должен$ быть отключен от $t$ . При инициализации алгоритм выполняет это требование, создавая предварительный поток $f$ , который насыщает все исходящие дуги $s$ , после чего $𝓁(v) = 0$ тривиально справедливо для всех $v ∈ V \ { s , t }$ . После инициализации алгоритм неоднократно выполняет применимую операцию отправки или изменения метки до тех пор, пока такие операции не будут применены, после чего предварительный поток преобразуется в максимальный поток.

generic-push-relabel(G, c, s, t):
    create a pre-flow f that saturates all out-arcs of s
    let 𝓁[s] = |V|
    let 𝓁[v] = 0 for all v ∈ V \ {s}
    while there is an applicable push or relabel operation do
        execute the operation

Корректность

Алгоритм поддерживает условие, что $𝓁$ является допустимой маркировкой во время его выполнения. В этом можно убедиться, изучив влияние операций push и relabel на функцию метки $𝓁$ . Операция перемаркировки увеличивает значение метки на соответствующий минимум плюс единицу, что всегда будет удовлетворять $ограничению 𝓁(u) \leq 𝓁(v) + 1$ . Операция push может отправить поток от $u$ к $v,$ если $𝓁(u) = 𝓁(v) + 1$ . Это может добавить $(v, u)$ к $G f$ и может удалить $(u, v)$ из $G f$ . Добавление $(v, u)$ к $G f$ не повлияет на допустимую маркировку, поскольку $𝓁(v) = 𝓁(u) - 1$ . Удаление $(u, v)$ из $G f$ удаляет соответствующее ограничение, поскольку допустимое свойство разметки $𝓁(u) \leq 𝓁(v) + 1$ применимо только к остаточным дугам в $G f$ . ^{[ 8 ]}

Если предпоток $f$ и допустимая разметка $𝓁$ для $f$ нет расширяющего пути от $s$ до $t$ существуют, то в остаточном графе $G f$ . Это можно доказать от противного, основанного на неравенствах, которые возникают в функции разметки, когда предполагается, что увеличивающий путь действительно существует. Если алгоритм завершается, то все узлы в $V \ { s , t }$ не активны. Это означает, что все $v ∈ V \ { s , t }$ не имеют избыточного потока, и без избытка предпоток $f$ подчиняется ограничению сохранения потока и может считаться нормальным потоком. Этот поток является максимальным потоком в соответствии с теоремой о максимальном потоке и минимальном сокращении, поскольку не существует увеличивающего пути от $s$ до $t$ . ^{[ 8 ]}

Следовательно, алгоритм вернет максимальный поток после завершения.

Временная сложность

Чтобы ограничить временную сложность алгоритма, мы должны проанализировать количество операций push и relabel, которые происходят в основном цикле. Количество операций перемаркировки, насыщающей отправки и ненасыщающей отправки анализируется отдельно.

В алгоритме операция перемаркировки может быть выполнена не более чем $(2| V | - 1)(| V | - 2) < 2| В | 2$ раз. Это связано с тем, что значение метки $𝓁(u)$ для любого узла u никогда не может уменьшаться, а максимальное значение метки не превышает $2| В | - 1$ для всех узлов. Это означает, что потенциально может быть выполнена операция изменения метки $2| В | - 1$ раз для всех узлов $V \ { s , t }$ (т. е. $| V | - 2$ ). Это приводит к оценке $O (V 2)$ для операции изменения метки.

на допустимую дугу $(u, v)$ удаляет дугу из $Gf .$ Каждое насыщающее нажатие Чтобы дуга была повторно вставлена в $G f$ для еще одного насыщающего нажатия, $сначала необходимо переименовать v$ , а затем нажать на дугу $(v, u)$ , затем $u$ необходимо перемаркировать . При этом $𝓁(u)$ увеличивается как минимум на два. Следовательно, существует $O (V)$ насыщающих нажатий на $(u, v)$ , а общее количество насыщающих нажатий не превосходит $2| В || Е |$ . Это приводит к ограничению времени $O (VE)$ для насыщающих операций push.

Ограничение количества ненасыщающих нажатий может быть достигнуто с помощью потенциального аргумента . Мы используем потенциальную функцию $Φ = Σ [u \in V \land x f (u) > 0] 𝓁(u)$ (т. е. $Φ$ — сумма меток всех активных узлов). Очевидно, что $изначально Φ$ равно $0$ и остается неотрицательным на протяжении всего выполнения алгоритма. И перемаркировка, и насыщение могут увеличить $Φ$ . Однако значение $Φ$ должно быть равно 0 при завершении, поскольку в конце выполнения алгоритма не может оставаться активных узлов. Это означает, что во время выполнения алгоритма ненасыщающие push-уведомления должны компенсировать разницу между операциями перемаркировки и насыщающими push-операциями, чтобы $Φ$ завершился со значением 0. Операция изменения метки может увеличить $Φ$ не более чем на $(2| V | - 1)(| V | - 2)$ . Насыщающее нажатие на $(u, v)$ активирует $v$ , если оно было неактивно до нажатия, увеличивая $Φ$ не более чем на $2| В | - 1$ . Следовательно, общий вклад всех насыщающих операций push в $Φ$ не превышает $(2| V | - 1)(2| V || E |)$ . Ненасыщающий толчок $(u, v)$ всегда деактивирует $u$ , но может также активировать $v,$ как при насыщающем толчке. В результате он уменьшает $Φ$ как минимум на $𝓁(u) - 𝓁(v) = 1$ . Поскольку перемаркировки и насыщающие нажатия увеличивают $Φ$ , общее количество ненасыщающих перемещений должно составлять разницу $(2| V | - 1)(| V | - 2) + (2| V | - 1)(2| V || Е |) \leq 4| В | 2 | Е |$ . Это приводит к временной границе $O (V 2 E)$ для ненасыщающих операций push.

В сумме алгоритм выполняет $O (V 2)$ перемаркировки, $O (VE)$ насыщающие нажатия и $O (V 2 Д)$ ненасыщающие толчки. Структуры данных могут быть спроектированы так, чтобы выбирать и выполнять применимую операцию за $время O (1)$ . Следовательно, временная сложность алгоритма равна $O (V 2 Е)$ . ^{[ 1 ]}^{[ 8 ]}

Пример

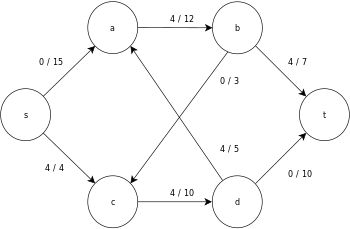
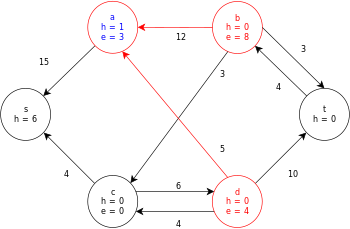
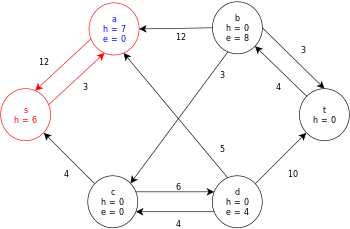
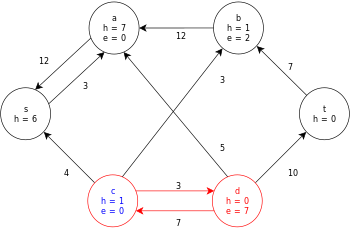
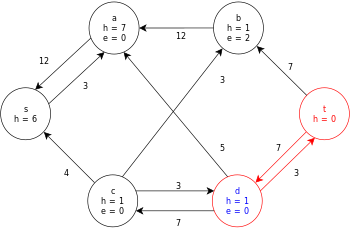
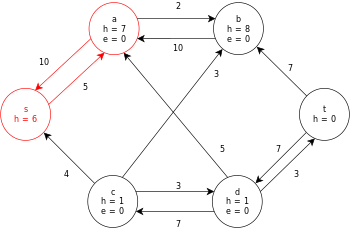
Ниже приведен пример выполнения общего алгоритма push-relabel, определенного выше, на следующей простой диаграмме сетевого потока.

Начальный граф сети потоков

Окончательный график сети максимального расхода

В примере значения h и e обозначают метку $𝓁$ и избыток $x f$ соответственно узла во время выполнения алгоритма. Каждый остаточный граф в примере содержит только остаточные дуги с емкостью больше нуля. Каждый остаточный граф может содержать несколько итераций цикла выполнения операции .

Алгоритм Операции	Остаточный график
Инициализируйте остаточный граф, установив для предварительного потока значения 0 и инициализировав маркировку.
Начальное насыщающее нажатие выполняется по всем дугам предварительного потока из источника, $s$ .
Узел $a$ переименовывается, чтобы направить избыточный поток к стоку $t$ . Избыток $a$ затем перемещается в $b,$ затем $в d$ в двух последующих насыщающих нажатиях; что все равно оставляет $a$ с некоторым избытком.

И снова $a$ переименовывается, чтобы сдвинуть его избыток вдоль последнего оставшегося положительного остатка (т. е. сдвинуть избыток обратно в $s$ ). Затем узел $a$ удаляется из набора активных узлов.

Переименуйте $b$ , а затем переместите его избыток в $t$ и $c$ .
Переименуйте $c,$ а затем переместите его избыток в $d$ .
Переименуйте $d,$ а затем переместите его избыток в $t$ .
В результате узел $b$ остается единственным оставшимся активным узлом, но он не может направить свой избыточный поток в сторону стока. Переименуйте $b$ , а затем переместите его избыток к источнику $s$ через узел $a$ .

Отправьте последний бит лишнего $назад$ к источнику, $s$ . Активных узлов не осталось. Алгоритм завершает работу и возвращает максимальный поток графа (как показано выше).

Пример (но с начальным потоком 0) можно запустить здесь в интерактивном режиме.

Практическая реализация

Хотя общий алгоритм push-relabel имеет $O (V 2 E)$ временная сложность, эффективные реализации достигают $O (V 3)$ или снизить временную сложность за счет применения соответствующих правил при выборе применимых операций отправки и изменения меток. Эмпирические результаты можно дополнительно улучшить с помощью эвристики.

Структура данных «Токовая дуга» и операция разряда

Структура данных «текущая дуга» представляет собой механизм посещения внутренних и внешних соседей узла в потоковой сети в статическом круговом порядке. Если для узла создается односвязный список соседей, структура данных может быть такой же простой, как указатель на список, который проходит через список и перематывается назад к началу, когда достигает конца.

На основе структуры данных «ток-дуга» можно определить операцию разряда. Операция разрядки применяется к активному узлу и неоднократно выталкивает поток из узла, пока он не станет неактивным, перемаркируя его по мере необходимости для создания в процессе допустимых дуг.

discharge(u):
    while x_f[u] > 0 do
        if current-arc[u] has run off the end of neighbors[u] then
            relabel(u)
            rewind current-arc[u]
        else
            let (u, v) = current-arc[u]
            if (u, v) is admissible then
                push(u, v)
            let current-arc[u] point to the next neighbor of u

Поиск следующего допустимого ребра для продвижения $O(1)$ амортизированная сложность . Указатель текущей дуги перемещается к следующему соседу только тогда, когда ребро текущего соседа насыщено или недопустимо, и ни одно из этих двух свойств не может измениться до тех пор, пока активный узел не $u$ перемаркируется. Следовательно, когда указатель убегает, допустимых ненасыщенных ребер нет и нам приходится перемаркировать активный узел. $u$ , поэтому переместив указатель $O(V)$ раз оплачивается за счет $O(V)$ операция перемаркировки. ^{[ 8 ]}

Правила выбора активного узла

Определение операции выгрузки сводит алгоритм push-relabel к многократному выбору активного узла для выгрузки. В зависимости от правила отбора алгоритм имеет различную временную сложность. Для краткости мы игнорируем $s$ и $t$ при упоминании узлов в следующем обсуждении.

Правило выбора ФИФО

Алгоритм FIFO принудительной перемаркировки ^{[ 2 ]} организует активные узлы в очередь. Начальные активные узлы можно вставлять в произвольном порядке. Алгоритм всегда удаляет узел в начале очереди на выгрузку. Всякий раз, когда неактивный узел становится активным, он добавляется в конец очереди.

Алгоритм имеет $O (V 3)$ временная сложность.

Правило выбора «Переименование на передний план»

Алгоритм перемаркировки на передний план ^{[ 1 ]} организует все узлы в связанный список и поддерживает инвариант, согласно которому список топологически отсортирован относительно допустимой сети. Алгоритм сканирует список спереди назад и выполняет операцию разрядки на текущем узле, если он активен. Если узел переименовывается, он перемещается в начало списка, и сканирование перезапускается с начала.

Алгоритм также имеет $O (V 3)$ временная сложность.

Правило выбора высшей метки

Алгоритм push-relabel с наивысшей меткой ^{[ 11 ]} организует все узлы в сегменты, индексированные по их меткам. Алгоритм всегда выбирает для выгрузки активный узел с наибольшей меткой.

Алгоритм имеет $O (V 2 \sqrt E)$ временная сложность. Если вместо этого используется правило выбора наименьшей метки, временная сложность становится $O (V 2 Е)$ . ^{[ 3 ]}

Методики реализации

Хотя в приведенном выше описании общего алгоритма push-relabel $𝓁(u)$ устанавливается равным нулю для каждого узла u, кроме $s$ и $t$ , в начале предпочтительнее выполнить обратный поиск в ширину от $t$ для вычисления точного значения. этикетки. ^{[ 2 ]}

Алгоритм обычно разделяется на два этапа. На первом этапе вычисляется максимальный предварительный поток, освобождая только активные узлы, метки которых меньше $n$ . На втором этапе максимальный предварительный поток преобразуется в максимальный поток, возвращая избыточный поток, который не может достичь $t,$ в $s$ . Можно показать, что вторая фаза имеет $временную сложность O (VE)$ независимо от порядка операций push и relabel и, следовательно, доминирует первой фазой. Альтернативно это можно реализовать с помощью декомпозиции потока. ^{[ 9 ]}

Эвристика имеет решающее значение для улучшения эмпирической эффективности алгоритма. ^{[ 12 ]} Двумя наиболее часто используемыми эвристиками являются эвристика разрыва и эвристика глобальной перемаркировки. ^{[ 2 ]}^{[ 13 ]} Эвристика пробелов обнаруживает пробелы в функции маркировки. Если существует метка 0 < 𝓁 ' < | В | для которого не существует узла $u$ такого, что $𝓁(u) = 𝓁'$ , то любой узел $u$ такой, что $𝓁' < 𝓁(u) < | В |$ был отключен от $t$ и может быть немедленно переименован в $(| V | + 1)$ . Эвристика глобальной перемаркировки периодически выполняет обратный поиск в ширину от $t$ в $G f$ для вычисления точных меток узлов. Обе эвристики пропускают бесполезные операции смены меток, которые являются узким местом алгоритма и способствуют неэффективности динамических деревьев. ^{[ 4 ]}

Примеры реализации

C- реализация

#include <stdlib.h>
#include <stdio.h>

#define NODES 6
#define MIN(X,Y) ((X) < (Y) ? (X) : (Y))
#define INFINITE 10000000

void push(const int * const * C, int ** F, int *excess, int u, int v) {
  int send = MIN(excess[u], C[u][v] - F[u][v]);
  F[u][v] += send;
  F[v][u] -= send;
  excess[u] -= send;
  excess[v] += send;
}

void relabel(const int * const * C, const int * const * F, int *height, int u) {
  int v;
  int min_height = INFINITE;
  for (v = 0; v < NODES; v++) {
    if (C[u][v] - F[u][v] > 0) {
      min_height = MIN(min_height, height[v]);
      height[u] = min_height + 1;
    }
  }
};

void discharge(const int * const * C, int ** F, int *excess, int *height, int *seen, int u) {
  while (excess[u] > 0) {
    if (seen[u] < NODES) {
      int v = seen[u];
      if ((C[u][v] - F[u][v] > 0) && (height[u] > height[v])) {
        push(C, F, excess, u, v);
      } else {
        seen[u] += 1;
      }
    } else {
      relabel(C, F, height, u);
      seen[u] = 0;
    }
  }
}

void moveToFront(int i, int *A) {
  int temp = A[i];
  int n;
  for (n = i; n > 0; n--) {
    A[n] = A[n-1];
  }
  A[0] = temp;
}

int pushRelabel(const int * const * C, int ** F, int source, int sink) {
  int *excess, *height, *list, *seen, i, p;

  excess = (int *) calloc(NODES, sizeof(int));
  height = (int *) calloc(NODES, sizeof(int));
  seen = (int *) calloc(NODES, sizeof(int));

  list = (int *) calloc((NODES-2), sizeof(int));

  for (i = 0, p = 0; i < NODES; i++){
    if ((i != source) && (i != sink)) {
      list[p] = i;
      p++;
    }
  }

  height[source] = NODES;
  excess[source] = INFINITE;
  for (i = 0; i < NODES; i++)
    push(C, F, excess, source, i);

  p = 0;
  while (p < NODES - 2) {
    int u = list[p];
    int old_height = height[u];
    discharge(C, F, excess, height, seen, u);
    if (height[u] > old_height) {
      moveToFront(p, list);
      p = 0;
    } else {
      p += 1;
    }
  }
  int maxflow = 0;
  for (i = 0; i < NODES; i++)
    maxflow += F[source][i];

  free(list);

  free(seen);
  free(height);
  free(excess);

  return maxflow;
}

void printMatrix(const int * const * M) {
  int i, j;
  for (i = 0; i < NODES; i++) {
    for (j = 0; j < NODES; j++)
      printf("%d\t",M[i][j]);
    printf("\n");
  }
}

int main(void) {
  int **flow, **capacities, i;
  flow = (int **) calloc(NODES, sizeof(int*));
  capacities = (int **) calloc(NODES, sizeof(int*));
  for (i = 0; i < NODES; i++) {
    flow[i] = (int *) calloc(NODES, sizeof(int));
    capacities[i] = (int *) calloc(NODES, sizeof(int));
  }

  // Sample graph
  capacities[0][1] = 2;
  capacities[0][2] = 9;
  capacities[1][2] = 1;
  capacities[1][3] = 0;
  capacities[1][4] = 0;
  capacities[2][4] = 7;
  capacities[3][5] = 7;
  capacities[4][5] = 4;

  printf("Capacity:\n");
  printMatrix(capacities);

  printf("Max Flow:\n%d\n", pushRelabel(capacities, flow, 0, 5));

  printf("Flows:\n");
  printMatrix(flow);

  return 0;
}

Python Реализация

Ссылки

^ Перейти обратно: ^а ^б ^с Кормен, TH ; Лейзерсон, CE ; Ривест, РЛ ; Штейн, К. (2001). «§26 Максимальный расход». Введение в алгоритмы (2-е изд.). Массачусетский технологический институт Пресс. стр. 643–698 . ISBN 978-0262032933 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Гольдберг А.В.; Тарьян, Р.Э. (1986). «Новый подход к проблеме максимального расхода». Материалы восемнадцатого ежегодного симпозиума ACM по теории вычислений – STOC '86 . п. 136. дои : 10.1145/12130.12144 . ISBN 978-0897911931 . S2CID 14492800 .
^ Перейти обратно: ^а ^б Ахуджа, Равиндра К.; Кодиалам, Мурали; Мишра, Аджай К.; Орлин, Джеймс Б. (1997). «Вычислительные исследования алгоритмов максимального расхода». Европейский журнал операционных исследований . 97 (3): 509. CiteSeerX 10.1.1.297.2945 . дои : 10.1016/S0377-2217(96)00269-X .
^ Перейти обратно: ^а ^б ^с Голдберг, Эндрю В. (2008). «Алгоритм частичного увеличения и перемаркировки для задачи максимального потока». Алгоритмы – ЕКА 2008 . Конспекты лекций по информатике. Том. 5193. стр. 466–477. CiteSeerX 10.1.1.150.5103 . дои : 10.1007/978-3-540-87744-8_39 . ISBN 978-3-540-87743-1 .
^ Гольдберг, Эндрю В. (1997). «Эффективная реализация масштабирующего алгоритма потока с минимальной стоимостью». Журнал алгоритмов . 22 : 1–29. дои : 10.1006/jagm.1995.0805 .
^ Ахуджа, Равиндра К.; Орлин, Джеймс Б. (1991). «Алгоритмы увеличения пути, направленные на расстояние, для задач максимального потока и параметрического максимального потока». Логистика военно-морских исследований . 38 (3): 413. CiteSeerX 10.1.1.297.5698 . doi : 10.1002/1520-6750(199106)38:3<413::AID-NAV3220380310>3.0.CO;2-J .
^ Гольдберг, Эндрю В.; Тарьян, Роберт Э. (2014). «Эффективные алгоритмы максимального расхода». Коммуникации АКМ . 57 (8): 82. дои : 10.1145/2628036 . S2CID 17014879 .
^ Перейти обратно: ^а ^б ^с ^д ^и Гольдберг, Эндрю В.; Тарьян, Роберт Э. (1988). «Новый подход к проблеме максимального потока» . Журнал АКМ . 35 (4): 921. дои : 10.1145/48014.61051 . S2CID 52152408 .
^ Перейти обратно: ^а ^б Ахуджа, РК; Маньянти, TL; Орлин, Дж. Б. (1993). Сетевые потоки: теория, алгоритмы и приложения (1-е изд.). Прентис Холл. ISBN 978-0136175490 .
^ Шилоах, Йоси; Вишкин, Узи (1982). «О (n2log n) параллельный алгоритм максимального потока». Журнал алгоритмов . 3 (2): 128–146. дои : 10.1016/0196-6774(82)90013-X .
^ Чериян, Дж.; Махешвари, С.Н. (1988). «Анализ алгоритмов предварительной подачи для максимального потока в сети». Основы программных технологий и теоретической информатики . Конспекты лекций по информатике. Том. 338. с. 30. дои : 10.1007/3-540-50517-2_69 . ISBN 978-3-540-50517-4 .
^ Черкасский Борис Владимирович; Гольдберг, Эндрю В. (1995). «О реализации метода push-relabel для задачи максимального потока». Целочисленное программирование и комбинаторная оптимизация . Конспекты лекций по информатике. Том. 920. с. 157. CiteSeerX 10.1.1.150.3609 . дои : 10.1007/3-540-59408-6_49 . ISBN 978-3-540-59408-6 .
^ Деригс, У.; Мейер, В. (1989). «Реализация алгоритма максимального потока Голдберга? Вычислительное исследование». Журнал исследования операций . 33 (6): 383. дои : 10.1007/BF01415937 . S2CID 39730584 .

[clrs26-1] Перейти обратно: ^а ^б ^с Кормен, TH ; Лейзерсон, CE ; Ривест, РЛ ; Штейн, К. (2001). «§26 Максимальный расход». Введение в алгоритмы (2-е изд.). Массачусетский технологический институт Пресс. стр. 643–698 . ISBN 978-0262032933 .

[goldberg86-2] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Гольдберг А.В.; Тарьян, Р.Э. (1986). «Новый подход к проблеме максимального расхода». Материалы восемнадцатого ежегодного симпозиума ACM по теории вычислений – STOC '86 . п. 136. дои : 10.1145/12130.12144 . ISBN 978-0897911931 . S2CID 14492800 .

[ahuja97-3] Перейти обратно: ^а ^б Ахуджа, Равиндра К.; Кодиалам, Мурали; Мишра, Аджай К.; Орлин, Джеймс Б. (1997). «Вычислительные исследования алгоритмов максимального расхода». Европейский журнал операционных исследований . 97 (3): 509. CiteSeerX 10.1.1.297.2945 . дои : 10.1016/S0377-2217(96)00269-X .

[goldberg08-4] Перейти обратно: ^а ^б ^с Голдберг, Эндрю В. (2008). «Алгоритм частичного увеличения и перемаркировки для задачи максимального потока». Алгоритмы – ЕКА 2008 . Конспекты лекций по информатике. Том. 5193. стр. 466–477. CiteSeerX 10.1.1.150.5103 . дои : 10.1007/978-3-540-87744-8_39 . ISBN 978-3-540-87743-1 .

[goldberg97-5] Гольдберг, Эндрю В. (1997). «Эффективная реализация масштабирующего алгоритма потока с минимальной стоимостью». Журнал алгоритмов . 22 : 1–29. дои : 10.1006/jagm.1995.0805 .

[ahuja91-6] Ахуджа, Равиндра К.; Орлин, Джеймс Б. (1991). «Алгоритмы увеличения пути, направленные на расстояние, для задач максимального потока и параметрического максимального потока». Логистика военно-морских исследований . 38 (3): 413. CiteSeerX 10.1.1.297.5698 . doi : 10.1002/1520-6750(199106)38:3<413::AID-NAV3220380310>3.0.CO;2-J .

[goldberg2014-7] Гольдберг, Эндрю В.; Тарьян, Роберт Э. (2014). «Эффективные алгоритмы максимального расхода». Коммуникации АКМ . 57 (8): 82. дои : 10.1145/2628036 . S2CID 17014879 .

[goldberg88-8] Перейти обратно: ^а ^б ^с ^д ^и Гольдберг, Эндрю В.; Тарьян, Роберт Э. (1988). «Новый подход к проблеме максимального потока» . Журнал АКМ . 35 (4): 921. дои : 10.1145/48014.61051 . S2CID 52152408 .

[amo93-9] Перейти обратно: ^а ^б Ахуджа, РК; Маньянти, TL; Орлин, Дж. Б. (1993). Сетевые потоки: теория, алгоритмы и приложения (1-е изд.). Прентис Холл. ISBN 978-0136175490 .

[sv82-10] Шилоах, Йоси; Вишкин, Узи (1982). «О (n2log n) параллельный алгоритм максимального потока». Журнал алгоритмов . 3 (2): 128–146. дои : 10.1016/0196-6774(82)90013-X .

[cheriyan88-11] Чериян, Дж.; Махешвари, С.Н. (1988). «Анализ алгоритмов предварительной подачи для максимального потока в сети». Основы программных технологий и теоретической информатики . Конспекты лекций по информатике. Том. 338. с. 30. дои : 10.1007/3-540-50517-2_69 . ISBN 978-3-540-50517-4 .

[cherkassky95-12] Черкасский Борис Владимирович; Гольдберг, Эндрю В. (1995). «О реализации метода push-relabel для задачи максимального потока». Целочисленное программирование и комбинаторная оптимизация . Конспекты лекций по информатике. Том. 920. с. 157. CiteSeerX 10.1.1.150.3609 . дои : 10.1007/3-540-59408-6_49 . ISBN 978-3-540-59408-6 .

[derigs89-13] Деригс, У.; Мейер, В. (1989). «Реализация алгоритма максимального потока Голдберга? Вычислительное исследование». Журнал исследования операций . 33 (6): 383. дои : 10.1007/BF01415937 . S2CID 39730584 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]