Суперперестановка

В комбинаторной математике суперперестановка строку n которая символов представляет собой , содержит каждую перестановку n символов в качестве подстроки . Хотя тривиальные суперперестановки могут просто состоять из каждой объединенной вместе перестановки, суперперестановки также могут быть короче (за исключением тривиального случая n = 1), поскольку допускается перекрытие. Например, в случае n = 2 суперперестановка 1221 содержит все возможные перестановки (12 и 21), но более короткая строка 121 также содержит обе перестановки.

Было показано, что для 1 ≤ n ≤ 5 наименьшая суперперестановка на n символах имеет длину 1! + 2! + … + н ! (последовательность A180632 в OEIS ). Первые четыре наименьшие суперперестановки имеют длину соответственно 1, 3, 9 и 33, образуя строки 1, 121, 123121321 и 123412314231243121342132413214321. Однако для n = 5 существует несколько наименьших суперперестановок, имеющих длину 153. Одна из таких суперперестановок: показано ниже, а другой такой же длины можно получить, поменяв местами все четверки и пятерки во второй половине строки (после жирного 2 ): ^[1]

1234512341523412534123541231452314253142351423154231245312435124315243125431 2 1345213425134215342135421324513241532413524132541321453214352143251432154321

Для случаев n > 5 еще не доказана наименьшая суперперестановка и не найден шаблон для их поиска, но для них найдены нижняя и верхняя границы.

Поиск суперперестановок

Схема создания суперперестановки с 3 символами из суперперестановки с 2 символами

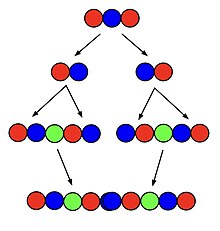
Один из наиболее распространенных алгоритмов создания суперперестановки порядка. $n$ это рекурсивный алгоритм. Во-первых, суперперестановка порядка $n-1$ разбивается на отдельные перестановки в том порядке, в котором они появлялись в суперперестановке. Каждая из этих перестановок затем помещается рядом с собственной копией с добавлением n- го символа между двумя копиями. Наконец, каждая полученная структура размещается рядом и все соседние одинаковые символы объединяются. ^[2]

Например, суперперестановка порядка 3 может быть создана из перестановки с двумя символами; начиная с суперперестановки 121 и разбивая ее на перестановки 12 и 21, перестановки копируются и помещаются как 12312 и 21321. Они складываются вместе, чтобы создать 1231221321, а идентичные соседние двойки в середине объединяются, чтобы создать 123121321, что действительно является суперперестановкой порядка 3. Этот алгоритм приводит к созданию кратчайшей возможной суперперестановки для всех n, меньших или равных 5, но становится все длиннее, чем самая короткая из возможных, по мере того, как n увеличивается сверх этого. ^[2]

Другой способ найти суперперестановки заключается в создании графа , в котором каждая перестановка является вершиной и каждая перестановка соединена ребром. каждым ребром связан вес С ; вес рассчитывается исходя из того, сколько символов можно добавить в конец одной перестановки (отбрасывая такое же количество символов из начала), чтобы получить другую перестановку. ^[2] Например, ребро от 123 до 312 имеет вес 2, потому что 123 + 12 = 12312 = 312. Любой гамильтонов путь через созданный граф является суперперестановкой, и проблема поиска пути с наименьшим весом становится формой коммивояжера . проблема . Первый экземпляр суперперестановки меньше длины $1!+2!+\ldots +n!$ был найден с помощью компьютерного поиска по этому методу Робином Хьюстоном.

Нижние границы, или проблема Харухи

В сентябре 2011 года анонимный плакат на Science & Math (« /sci/ ») доске сайта 4chan доказал, что наименьшая суперперестановка n символов ( n ≥ 2) имеет длину не менее n ! + ( n −1)! + ( n −2)! + п - 3. ^[3] В отношении японского аниме- сериала «Меланхолия Харухи Судзумии » проблема была представлена на имиджборде как «Проблема Харухи»: ^[4] Если бы вы хотели посмотреть 14 серий первого сезона сериала во всех возможных порядках, какую самую короткую цепочку серий вам нужно было бы посмотреть? ^[5] Доказательство этой нижней границы привлекло внимание широкой общественности в октябре 2018 года, после того как математик и ученый-компьютерщик Робин Хьюстон написал об этом в Твиттере. ^[3] 25 октября 2018 года Робин Хьюстон, Джей Пантон и Винс Ваттер опубликовали уточненную версию этого доказательства в Онлайн-энциклопедии целочисленных последовательностей (OEIS). ^[5]^[6] Опубликованная версия этого доказательства, приписываемая «Анонимному плакату 4chan», появляется в Engen and Vatter ( 2021 ). ^[7]В частности, для «Проблемы Харухи» (случай с 14 символами) текущие нижняя и верхняя границы составляют 93 884 313 611 и 93 924 230 411 соответственно. ^[3] Это означает, что просмотр сериала во всех возможных порядках потребует около 4,3 миллиона лет. ^[8]

Верхние границы

20 октября 2018 года, адаптировав конструкцию Аарона Уильямса для построения гамильтоновых путей через граф Кэли группы симметричной , ^[9] Писатель-фантаст и математик Грег Иган разработал алгоритм для создания суперперестановок длины n ! + ( n −1)! + ( n −2)! + ( n −3)! + п - 3. ^[2] До 2018 года это были самые маленькие суперперестановки, известные для n ≥ 7. Однако 1 февраля 2019 года Богдан Коанда объявил, что нашел суперперестановку для n = 7 длины 5907, или ( n ! + ( n −1)! + ( n −2)! + ( n −3)! + n − 3) − 1, что стало новым рекордом. ^[2] 27 февраля 2019 года, используя идеи Робина Хьюстона, Иган создал суперперестановку для n = 7 длиной 5906. ^[2] Существуют ли подобные более короткие суперперестановки для значений n > 7, остается открытым вопросом. Текущая лучшая нижняя граница (см. раздел выше) для n = 7 по-прежнему равна 5884.

См. также

Супершаблон — перестановка, содержащая каждую перестановку из n символов в качестве шаблона перестановки.
Последовательность Де Брейна , аналогичная проблема с циклическими последовательностями

Дальнейшее чтение

Эшлок, Дэниел А.; Тиллотсон, Дженетт (1993), «Построение малых суперперестановок и минимальных инъективных суперструн», Congressus Numerantium , 93 : 91–98, Zbl 0801.05004
Анонимный постер 4chan; Хьюстон, Робин; Пантоне, Джей; Ваттер, Винс (25 октября 2018 г.). «Нижняя граница длины кратчайшего супершаблона» (PDF) . Электронная энциклопедия целочисленных последовательностей . {{cite journal}}: CS1 maint: числовые имена: список авторов ( ссылка )

Ссылки

^ Джонстон, Натаниэль (28 июля 2013 г.). «Неединственность минимальных суперперестановок» . Дискретная математика . 313 (14): 1553–1557. arXiv : 1303.4150 . Бибкод : 2013arXiv1303.4150J . дои : 10.1016/j.disc.2013.03.024 . S2CID 12018639 . Збл 1368.05004 . Проверено 16 марта 2014 г.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж Иган, Грег (20 октября 2018 г.). «Супермутации» . www.gregegan.net . Проверено 15 января 2020 г. .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Григгс, Мэри Бет. «Анонимный пост на 4chan может помочь разгадать математическую загадку 25-летней давности » Грань .
^ 17 сентября 2011 г.) перестановок III возле любви» . « Нить Анон, — Сан (
↑ Перейти обратно: Перейти обратно: ^а ^б Кларрайх, Эрика (5 ноября 2018 г.). «Писатель-фантаст Грег Иган и анонимный математический гений решают задачу перестановки» . Журнал Кванта . Проверено 21 июня 2020 г.
^ Анонимный постер 4chan; Хьюстон, Робин; Пантоне, Джей; Ваттер, Винс (25 октября 2018 г.). «Нижняя граница длины кратчайшего супершаблона» (PDF) . ОЭИС . Проверено 27 октября 2018 г. {{cite web}}: CS1 maint: числовые имена: список авторов ( ссылка )
^ Энген, Майкл; Ваттер, Винсент (2021), «Содержит все перестановки», American Mathematical Monthly , 128 (1): 4–24, arXiv : 1810.08252 , doi : 10.1080/00029890.2021.1835384
^ Сполдинг, Кэти (30 октября 2018 г.). «4chan только что разгадал математическую загадку десятилетней давности» . IFLНаука . Проверено 5 октября 2023 г.
^ Аарон, Уильямс (2013). «Гамильтонность орграфа Кэли на симметрической группе, порожденной σ = (1 2 ... n) и τ = (1 2)». arXiv : 1307.2549v3 [ math.CO ].

Внешние ссылки

Задача минимальной суперперестановки - блог Натаниэля Джонстона
Грайм, Джеймс. «Супермутации – Числофил» (видео) . Ютуб . Брэйди Харан . Проверено 1 февраля 2018 г.
Оригинальный пост 4chan на /sci/ , заархивирован на warosu.org.
Твит Робина Хьюстона, который привлек внимание к посту на 4chan.
Статья о проблеме поиска коротких суперперестановок в журнале Quanta Magazine.

[1] Джонстон, Натаниэль (28 июля 2013 г.). «Неединственность минимальных суперперестановок» . Дискретная математика . 313 (14): 1553–1557. arXiv : 1303.4150 . Бибкод : 2013arXiv1303.4150J . дои : 10.1016/j.disc.2013.03.024 . S2CID 12018639 . Збл 1368.05004 . Проверено 16 марта 2014 г.

[Greg_Egan-2] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж Иган, Грег (20 октября 2018 г.). «Супермутации» . www.gregegan.net . Проверено 15 января 2020 г. .

[:0-3] Перейти обратно: Перейти обратно: ^а ^б ^с Григгс, Мэри Бет. «Анонимный пост на 4chan может помочь разгадать математическую загадку 25-летней давности » Грань .

[4] 17 сентября 2011 г.) перестановок III возле любви» . « Нить Анон, — Сан (

[:1-5] Перейти обратно: Перейти обратно: ^а ^б Кларрайх, Эрика (5 ноября 2018 г.). «Писатель-фантаст Грег Иган и анонимный математический гений решают задачу перестановки» . Журнал Кванта . Проверено 21 июня 2020 г.

[6] Анонимный постер 4chan; Хьюстон, Робин; Пантоне, Джей; Ваттер, Винс (25 октября 2018 г.). «Нижняя граница длины кратчайшего супершаблона» (PDF) . ОЭИС . Проверено 27 октября 2018 г. {{cite web}}: CS1 maint: числовые имена: список авторов ( ссылка )

[engenvatter-7] Энген, Майкл; Ваттер, Винсент (2021), «Содержит все перестановки», American Mathematical Monthly , 128 (1): 4–24, arXiv : 1810.08252 , doi : 10.1080/00029890.2021.1835384

[8] Сполдинг, Кэти (30 октября 2018 г.). «4chan только что разгадал математическую загадку десятилетней давности» . IFLНаука . Проверено 5 октября 2023 г.

[9] Аарон, Уильямс (2013). «Гамильтонность орграфа Кэли на симметрической группе, порожденной σ = (1 2 ... n) и τ = (1 2)». arXiv : 1307.2549v3 [ math.CO ].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]