Уравнение коллинеарности

Лучи света, проходящие через отверстие камеры-обскуры

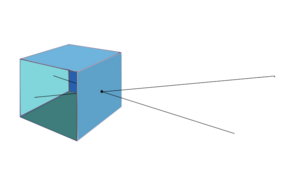
Уравнения коллинеарности представляют собой набор двух уравнений, используемых в фотограмметрии и компьютерном стереозрении для связи координат в плоскости датчика (в двух измерениях) с координатами объекта (в трех измерениях). Уравнения возникают из центральной проекции точки объекта через оптический центр камеры . на изображение на плоскости датчика

Три точки P, Q и R проецируются на плоскость S через центр проекции C.

оси x и z проекции P через центр проекции C

Определение

Пусть x, y и z относятся к системе координат с осями x и y в плоскости датчика. Обозначим координаты точки P на объекте через $x_{P},y_{P},z_{P}$, координаты точки изображения P на плоскости датчика через x и y и координаты проекционного (оптического) центра через $x_{0},y_{0},z_{0}$. Как следствие метода проекции существует то же фиксированное соотношение $\lambda$ между $x-x_{0}$ и $x_{0}-x_{P}$, $y-y_{0}$ и $y_{0}-y_{P}$, а расстояние центра проекции до плоскости датчика $z_{0}=c$ и $z_{P}-z_{0}$. Следовательно:

$x-x_{0}=-\lambda (x_{P}-x_{0})$

$y-y_{0}=-\lambda (y_{P}-y_{0})$

$c=\lambda (z_{P}-z_{0}),$

Решение для $\lambda$ в последнем уравнении и введя его в остальные, получим:

$x-x_{0}=-c\ {\frac {x_{P}-x_{0}}{z_{P}-z_{0}}}$

$y-y_{0}=-c\ {\frac {y_{P}-y_{0}}{z_{P}-z_{0}}}$

Точка P обычно задается в некоторой системе координат «вне» камеры координатами X , Y и Z , а центр проекции — $X_{0},Y_{0},Z_{0}$. Эти координаты могут быть преобразованы посредством вращения и перевода в систему камеры. Перевод не влияет на разницу координат, а вращение, часто называемое преобразованием камеры , задается матрицей R 3×3 , преобразующей $(X-X_{0},Y-Y_{0},Z-Z_{0})$ в:

$x_{P}-x_{0}=R_{11}(X-X_{0})+R_{21}(Y-Y_{0})+R_{31}(Z-Z_{0})$

$y_{P}-y_{0}=R_{12}(X-X_{0})+R_{22}(Y-Y_{0})+R_{32}(Z-Z_{0})$

и

$z_{P}-z_{0}=R_{13}(X-X_{0})+R_{23}(Y-Y_{0})+R_{33}(Z-Z_{0})$

Замена этих выражений приводит к системе двух уравнений, известных как уравнения коллинеарности :

$x-x_{0}=-c\ {\frac {R_{11}(X-X_{0})+R_{21}(Y-Y_{0})+R_{31}(Z-Z_{0})}{R_{13}(X-X_{0})+R_{23}(Y-Y_{0})+R_{33}(Z-Z_{0})}}$

$y-y_{0}=-c\ {\frac {R_{12}(X-X_{0})+R_{22}(Y-Y_{0})+R_{32}(Z-Z_{0})}{R_{13}(X-X_{0})+R_{23}(Y-Y_{0})+R_{33}(Z-Z_{0})}}$

Наиболее очевидное использование этих уравнений — для изображений, записанных камерой. В этом случае уравнение описывает преобразования пространства объекта (X, Y, Z) в координаты изображения (x, y). Он формирует основу для уравнений, используемых при корректировке пакета . Они указывают на то, что точка изображения (на сенсорной пластине камеры), наблюдаемая точка (на объекте) и центр проекции камеры были совмещены при съемке изображения.

См. также

• 3D-проекция
• Эпиполярная геометрия
• Модель камеры-обскуры