Дефазировка
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
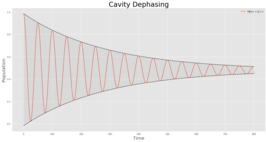
В физике классическое дефазировка — это механизм, который восстанавливает поведение квантовой системы . Это относится к тому, как когерентность , вызванная возмущением, со временем затухает, и система возвращается в состояние до возмущения. Это важный эффект в молекулярной и атомной , а также в физике конденсированного состояния мезоскопических спектроскопии устройств.
Причину можно понять, описав проводимость в металлах как классическое явление с квантовыми эффектами, заключенными в эффективную массу , которую можно вычислить квантово-механически, а также сопротивление , которое можно рассматривать как рассеяния эффект электронов проводимости . Когда температура снижается и размеры устройства значительно уменьшаются, это классическое поведение должно исчезнуть, и законы квантовой механики должны управлять поведением проводящих электронов, рассматриваемых как волны, которые баллистически движутся внутри проводника без какой-либо диссипации. Большую часть времени это то, что можно наблюдать. Но это оказалось неожиданностью [ кому? ] обнаружить, что так называемое время дефазировки , то есть время, необходимое проводящим электронам для потери своего квантового поведения, становится конечным, а не бесконечным, когда температура приближается к нулю в мезоскопических устройствах, нарушая ожидания теории Бориса Альтшулера , Аркадий Аронов и Давид Э. Хмельницкий. [1] Такое насыщение времени дефазировки при низких температурах является открытой проблемой, хотя было выдвинуто несколько предложений.
Когерентность выборки объясняется недиагональными элементами матрицы плотности . Внешнее электрическое или магнитное поле может создавать когерентность между двумя квантовыми состояниями в образце, если частота соответствует энергетической щели между двумя состояниями. Члены когерентности затухают со временем дефазировки или спин-спиновой релаксации T 2 .
После создания в образце когерентности светом образец излучает волну поляризации , частота которой равна и фаза которой инвертирована относительно падающего света. Кроме того, образец возбуждается падающим светом и генерируется популяция молекул в возбужденном состоянии. Свет, проходящий через образец, поглощается в результате этих двух процессов и выражается спектром поглощения . Когерентность затухает с увеличением постоянной времени T 2 , и интенсивность волны поляризации уменьшается. Заселенность возбужденного состояния также затухает с постоянной времени релаксации продольной T 1 . Постоянная времени T 2 обычно намного меньше, чем T 1 , а ширина полосы спектра поглощения связана с этими постоянными времени преобразованием Фурье , поэтому постоянная времени T 2 вносит основной вклад в ширину полосы. Постоянная времени T 2 была измерена напрямую с помощью сверхбыстрой спектроскопии с временным разрешением , например, в экспериментах с фотонным эхом .
Какова скорость дефазировки частицы с энергией E , если она находится в изменяющейся среде с температурой T ? В частности, какова скорость дефазировки, близкая к равновесной ( E~T ), и что происходит в пределе нулевой температуры? Этот вопрос интересовал мезоскопическое сообщество в течение последних двух десятилетий (см. ссылки ниже).
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Альтшулер, Б.Л.; Аронов, А.Г.; Хмельницкий, Д.Э. (30 декабря 1982 г.). «Влияние электрон-электронных столкновений с малой передачей энергии на квантовую локализацию» . Журнал физики C: Физика твердого тела . 15 (36): 7367–7386. Бибкод : 1982JPhC...15.7367A . дои : 10.1088/0022-3719/15/36/018 . ISSN 0022-3719 .
Другой
[ редактировать ]- Имри, Ю. (1997). Введение в мезоскопическую физику . Издательство Оксфордского университета . (И ссылки там.)
- Алейнер, Иллинойс; Альтшулер, Б.Л.; Гершенсон, МЭ (1999). «Комментарий к статье «Квантовая декогеренция в неупорядоченных мезоскопических системах» ». Письма о физических отзывах . 82 (15): 3190. arXiv : cond-mat/9808078 . Бибкод : 1999PhRvL..82.3190A . дои : 10.1103/PhysRevLett.82.3190 . S2CID 119348960 .
- Коэн, Д.; Имри, Ю. (1999). «Дефазировка при низких температурах». Физический обзор B . 59 (17): 11143–11146. arXiv : cond-mat/9807038 . Бибкод : 1999PhRvB..5911143C . дои : 10.1103/PhysRevB.59.11143 . S2CID 51856292 .
- Голубев Д.С.; Шен, Г.; Заикин А.Д. (2003). «Низкотемпературная дефазировка и перенормировка в модельных системах». Журнал Физического общества Японии . 72 (Приложение А): 30–35. arXiv : cond-mat/0208548 . Бибкод : 2003JPSJ...72S..30S . дои : 10.1143/JPSJS.72SA.30 . S2CID 119036267 .
- Саминадаяр, Л.; Моханти, П.; Уэбб, РА; Деджованни, П.; Бауэрле, К. (2007). «Электронная когерентность при низких температурах: роль магнитных примесей». Физика Э. 40 (1): 12–24. arXiv : 0709.4663 . Бибкод : 2007PhyE...40...12S . дои : 10.1016/j.physe.2007.05.026 . S2CID 13883162 .
- Моханти, П. (2001). «О декогерентных электронах и неупорядоченных проводниках». В Скьельторпе, Австрия; Вичек, Т. (ред.). Сложность от микроскопического к макроскопическому масштабу: согласованность и большие отклонения . Клювер . arXiv : cond-mat/0205274 . Бибкод : 2002cond.mat..5274M .
- Фраска, М. (2003). «Насыщение времени дефазировки в мезоскопических устройствах, изготовленных из ферромагнитного состояния». Физический обзор B . 68 (19): 193413. arXiv : cond-mat/0308377 . Бибкод : 2003PhRvB..68s3413F . дои : 10.1103/PhysRevB.68.193413 . S2CID 119498061 .