Гребенчатая сортировка

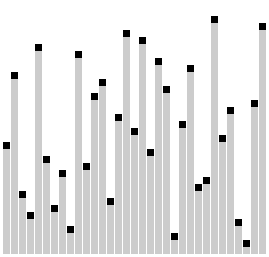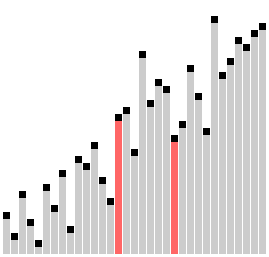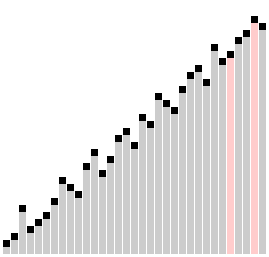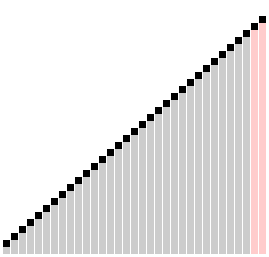Гребенчатая сортировка

Гребенчатая сортировка с коэффициентом сжатия k = 1,24733
Сорт	Алгоритм сортировки
Структура данных	Множество
Худшая производительность	$O(n^{2})$
Лучшая производительность	$\Theta (n\log n)$
Средняя производительность	$\Omega (n^{2}/2^{p})$, где p — количество приращений
Наихудшая пространственная сложность	$O(1)$

Гребенчатая сортировка — это относительно простой алгоритм сортировки, первоначально разработанный Влодзимежем Добосевичем и Артуром Боровым в 1980 году. позже заново открыт (и получил название «Combsort») Стивеном Лейси и Ричардом Боксом в 1991 году. Гребенчатая сортировка улучшает сортировку пузырьком так же, как сортировка Шелл улучшает сортировку вставками , поскольку обе они позволяют элементам, которые начинаются далеко от их предполагаемой позиции, перемещаться более чем на одно пространство за перестановку.

nist.gov В определении «сортировка с убывающим приращением» термин «гребенчатая сортировка» упоминается как визуализация итеративных проходов данных, «там, где соприкасаются зубья гребенки»; первый термин связан с Доном Кнутом .

Алгоритм

Основная идея состоит в том, чтобы исключить черепахи или небольшие значения в конце списка, поскольку при пузырьковой сортировке они значительно замедляют сортировку. Кролики , большие значения в начале списка, не создают проблем при пузырьковой сортировке.

При пузырьковой сортировке при сравнении любых двух элементов между ними всегда имеется зазор (расстояние друг от друга), равный 1. Основная идея гребенчатой ​​сортировки заключается в том, что разрыв может быть намного больше 1. Внутренний цикл пузырьковой сортировки, который выполняет фактическую замену , модифицируется таким образом, что разрыв между замененными элементами уменьшается (для каждой итерации внешнего цикла) в шаги «коэффициента сжатия» k : [ ⁠ n / k ⁠ , ⁠ н / к ² ⁠ , ⁠ н / к ³ ⁠ , ..., 1] .

списка n Промежуток начинается с деления длины сортируемого на коэффициент сжатия k (обычно 1,3; см. ниже), и к этому промежутку применяется один проход вышеупомянутой модифицированной пузырьковой сортировки. Затем разрыв снова делится на коэффициент сжатия, список сортируется с использованием этого нового пробела, и процесс повторяется до тех пор, пока разрыв не станет равным 1. На этом этапе гребенчатая сортировка продолжается с использованием пробела, равного 1, пока список не будет полностью отсортирован. Таким образом, заключительный этап сортировки эквивалентен пузырьковой сортировке, но к этому времени с большинством черепах уже покончено, поэтому пузырьковая сортировка будет эффективной.

Фактор усадки оказывает большое влияние на эффективность гребенчатой ​​сортировки. Добосевич предложил k = 4/3 = 1,333…, в то время как Лейси и Бокс предложили 1,3 в качестве идеального коэффициента сжатия после эмпирического тестирования более чем 200 000 случайных списков длиной примерно 1000. Слишком маленькое значение замедляет работу алгоритма из-за излишне большого количества сравнений, тогда как слишком большое значение не позволяет эффективно справиться с черепахами, поэтому требуется много проходов с интервалом 1.

Схема повторных проходов сортировки с уменьшением промежутков аналогична сортировке Шелла, но в сортировке Шелл массив полностью сортируется на каждом проходе, прежде чем перейти к следующему наименьшему промежутку. Проходы гребенчатой ​​сортировки не полностью сортируют элементы. По этой причине последовательности пробелов сортировки Шелла имеют более высокий оптимальный коэффициент сжатия, составляющий около 2,25.

Еще одним уточнением, предложенным Лейси и Боксом, является «правило 11»: всегда используйте размер промежутка 11, округляя размеры промежутков 9 или 10 (достигаемые путем деления промежутков 12, 13 или 14 на 1,3) до 11. Это уничтожает черепах, доживших до последнего прохода пробела-1.

Псевдокод

function combsort(array input) is

    gap := input.size // Initialize gap size
    shrink := 1.3 // Set the gap shrink factor
    sorted := false

    loop while sorted = false
        // Update the gap value for a next comb
        gap := floor(gap / shrink)
        if gap ≤ 1 then
            gap := 1
            sorted := true // If there are no swaps this pass, we are done
        else if gap = 9 or gap = 10 then
            gap := 11      // The "rule of 11"
        end if

        // A single "comb" over the input list
        i := 0
        loop while i + gap < input.size // See Shell sort for a similar idea
            if input[i] > input[i+gap] then
                swap(input[i], input[i+gap])
                sorted := false
                // If this assignment never happens within the loop,
                // then there have been no swaps and the list is sorted.
             end if
    
             i := i + 1
         end loop
     end loop
end function

См. также

• Пузырьковая сортировка , как правило, более медленный алгоритм, является основой гребенчатой ​​сортировки.
• Коктейльная сортировка , или двунаправленная пузырьковая сортировка, представляет собой разновидность пузырьковой сортировки, которая также решает проблему черепах, хотя и менее эффективно.